Повторное использование .

Пусть алфавит А – числа (0, …, n -1)

Гаммирование по модулю n – пусть их зашифровали с помощью одной .

Пусть в распоряжении аналитика оказались две криптограммы, полученные наложением одной и той же гаммы на два разных открытых текста:

- два открытых текста;

- наложенная гамма;

- полученные закрытые тексты (криптограммы);

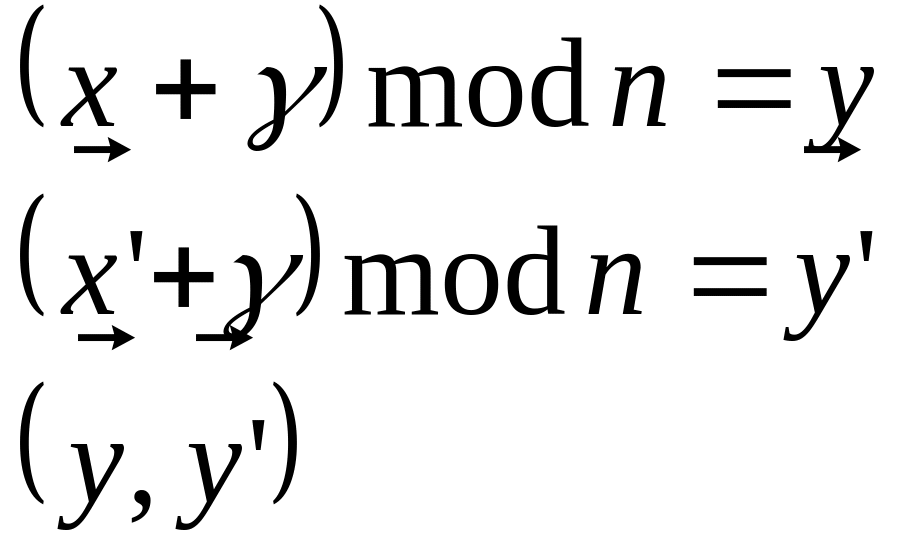
Рассмотрим возможности криптоаналитика по восстановлению открытых текстов:

Обозначим - расшифрование открытых текстов.

Если мы знаем один открытый текст или догадываемся, то

В любой переписке мы начинаем письмо со стандартных фраз типа «Здравствуйте», и если произвести грамотный подбор, то можно найти , а следовательно расшифровать текст. Этот метод использовался ранее, однако, можно использовать сейчас.

Избыточность языка.

Энтропия

Шеннон предложил признать формулу:

прирост информации = равен устранённой неопределённости.

Энтропия служит количественной мерой неопределённости случайного эксперимента.

Прямая и обратная теоремы относительно (?) источника кодирования.

Если есть какой-то источник, то минимальная длинна сообщения на выходе этого источника будет равна энтропии этого источника.

Рассмотрим среднюю информацию на одну букву языка.

 - язык;

- энтропия на знак  (средняя информация каждого знака)

Каждый знак несёт максимальную информацию.

В русском языке буквы появляются с разной вероятностью.

.

( - когда каждый знак появляется с равной вероятностью).

Для английского языка.

Будем полагать:

Для r стоящих рядом букв:

Энтропия языка :

- принято за среднюю энтропию на знак языка (r – не такое большое, хотя и …).

При этом было сказано

Каждый знак не доносит:

информации.

А если разделить:

,

то мы поучим избыточность - какое количество букв мы можем выбросить, не потеряв смысл текста.

			Комментарий
Разговорный	1,4	72%	Можно подобрать систему кодирования таким образом, что без потерь информации можем 100 букв зашифровать 100 букв в 28, то есть сжатие 4 раза.
Литературный	1,19	76%	- || -
Деловой	0,83	83,4%	- || -

Основы криптографии 13.10.05

Расстояние единственности.

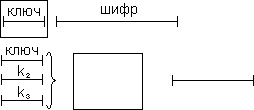
Предположим, что есть некоторый шифратор, у которого есть ключ, шифратор выдаёт шифр , присутствует алгоритм шифрования. Когда мы перехватили посылку, будем перебирать ключи, пока не найдём тот единственный ключ. Но может возникнуть ситуация, когда при небольших длинах криптограмм результат её расшифрования может дать несколько осмысленных текстов на разных ключах. Например криптограмму WNAJW, полученную при использовании сдвигового шифра для английского языка, порождают два открытых текста RIVER и ARENA, отвечающих ключам F (5) и W (22).

Проблемы:

• Какой длинны нужно иметь шифр , чтобы мы однозначно восстановили ключ?

Этим вопросом мы и займёмся:

Предположим, что на всех множествах X, Y, K задано распределение вероятности P(X), P(Y), P(K), а нас интересует , какая информация в шифре y содержится от ключа k.

Так как у нас ключ выбирается независимо от открытого текста.

- однозначно определяют друг друга

Распишем условную энтропию двух вероятностных распределений:

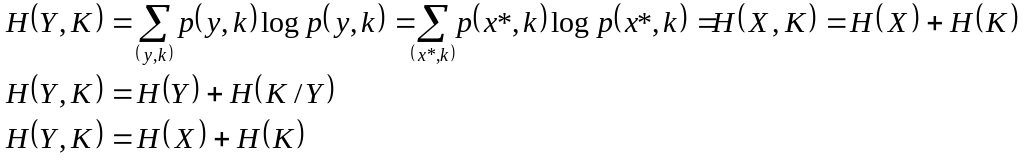
Из этих равенств следует:

- информация в шифртексте относительно ключа k.

Вот как можно эту информацию подсчитать. Эта формула позволит нам получить оценку среднего числа ложных ключей.

Рассмотрим поточный шифр , для которого множество X открытых текстов представляет собой множество возможных осмысленных текстов в данном алфавите А, состоящим из n букв. Зафиксируем некоторое число и будем интересоваться числом ложных ключей, отвечающих данной криптограмме.

- множество ключей k для которых .

Пусть

A – алфавит, длинны открытых шифр текстов одинаково равны L.

Пусть: знаем y, знаем множество ключей при условии y – шифр текст.

Число ложных ключей K(y)-1 – так как из всего множества один точно истинный.

Среднее число ложных ключей (математическое ожидание):

Теорема: для любого рассматриваемого шифра с равновероятными ключами при достаточно больших значениях L имеет место асимптотическое неравенство.

n =|A|– мощность.

- избыточность языка.

Доказательство:

Так как

В данном случае H(X) просто совпадает.

Так как - энтропия языка.

Если L достаточно большое (>50) можно записать это равенство как:

- асимптотическое равенство

Так как

Отсюда, а также из формулы (информация в шифр тексте относительно ключа k) следует:

Рассмотрим:

Функция выпуклая, следовательно для неё верно неравенство Иенсона.

Для нашего случая:

- количество ложных вариантов +1

- то, что мы получили в итоге.

Суммируя мы получили (как ранее было получено ):

Определение: расстоянием единственности для шифра называется наименьшее натуральное число , для которого число ложных ключей .

20.10.05

Максимальное значение будет при

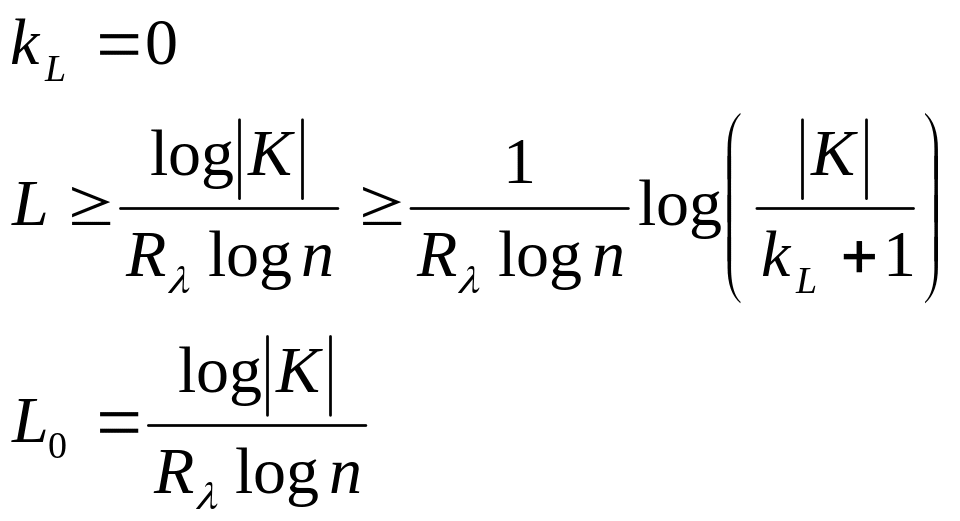
– оценка расстояния единственности.

Обычно(если двоичный случай):

Для русского языка расстояние единственности:

- шифр текст должен быть 1,39 больше длинны ключа для однозначного определения.