Чт, сен 08 2005 09:50:41

Основа криптографии.

Крипто - скрытое;

Граф - письмо.

Появилась задолго до римской империи.

1. Линейка Энея. Шифры перестановки. Шифр "Сцитала".

Линейка Энея

Узелки на верёвке делались напротив букв, после этого верёвка отправлялась получателю.

Шифр Сциталя

Ремень наматывается вокруг бревна, пишем что-то важное вдоль бревна, по букве на каждый оборот ремня, а затем заполняем свободное пространство случайным образом, далее ремень сматывался, отправлялся, а у получателя было такое же бревно.

Диск Альберти.

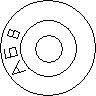
Внутренний диск двигается относительно внешнего, написаны буквы и запоминаем сдвиг диска. Отправитель и получатель договариваются о первой индексной букве. При шифровании сообщения отправитель ставил индексную букву против любой буквы большего диска. Эта буква записывалась в качестве первой буквы шифртекста.

Квадрат Полибия.

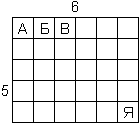
Я=(5,6)

Б=(1,2).

Литература:

"Основы криптографии" Алфёров, Зубков, Черёмушкин.

"Криптография" Бабаш, Шанкин.

2. Системы подстановок. Подстановка Цезаря. Система шифрования Вижинера. Книжные шифры.

Шифр Юлия Цезаря.

а, б, в,... я

1, 2, 3,... 30

Следует менять буквы так, чтобы из них не складывалось ни одного слова. Чтобы разобрать и прочитать их нужно читать всякий раз четвёртую букву вместо первой, например Г вместо А и так далее. Таким образом Цезарь заменял буквы в соответствии с подстановкой, нижняя строка которой представляет собой алфавит открытого текста, сдвинутый циклически на три буквы влево.

Х - буква открытого текста

...

Шифр Виженера

Использует таблицу в основе которой циклически сдвигаемые алфавиты:

Первая строка служит алфавитом открытого текста, а первый столбец алфавитом ключа. В качестве ключа используется открытый текст, к которому добавляется в качестве первой буквы, известной и отправителю и получателю.

Пример:

Известная буква Ж открытый текст МАШИНА:

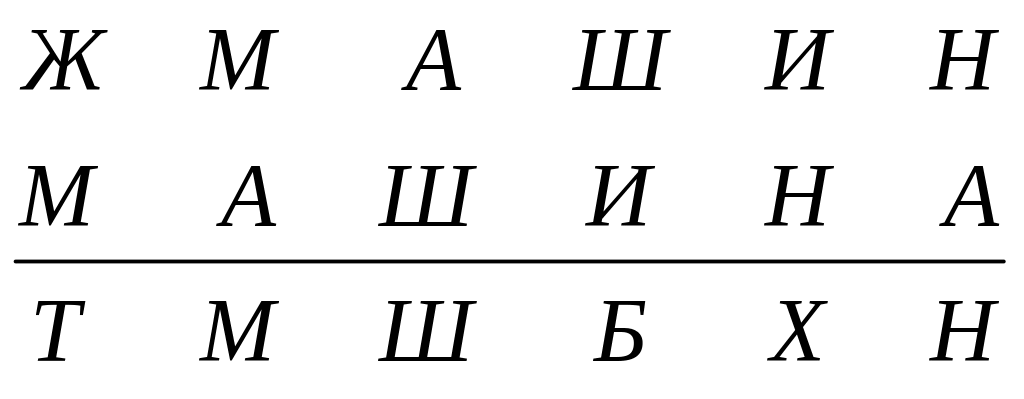
Шифртекст: ТМШБХН.

Позже была разработана формула, воспроизводящая зашифрование по Виженеру:

y=(x+k) mod 30

(это выражение обозначает остаток от деления на 30 от суммы в скобках),

где y – буква шифртекста, x – буква открытого текста, k – буква ключа.

Букв алфавита заменяются числами согласно следующей таблице:

Книжный шифр.

При шифровании достаточно больших объёмов текста возможно использование вместо ключа заранее оговорённого отрывка из художественной литературы.

3. Определение шифра. Шифры замены, перестановок, гаммирования.

Термины:

Открытая текст - исходная информация для передачи по каналу связи.

Шифр текст - последовательность знаков полученных в результате применения шифр. преобразований к открытому тексту.

Шифр – взаимнооднозначное преобразование открытого текста в шифртекст в зависимости от ключа криптосистемы.

Криптосистема – система шифр. преобразований, каждому из которых поступает во взаимно однозначное соответствие определённое значение параметра (ключа) криптосистемы.

Ключ криптосистемы – совокупность значений параметров, каждый из которых соответствует конкретному шифр преобразованию из КС (криптосистемы).

Открытый канал связи – канал связи, по которому передаётся только открытая информация.

Закрытый канал связи – канал связи, по которому передаются только шифр тексты.

Стойкость криптосистемы – способность её противостоять математическим (?) методам вычисления ключа и последующему (?) раскрытию соод. шифр текста.

Компрометация информации (ключа) – событие, в результате которого информация (ключ) может стать известной посторонним лицам.

Чт, сен 15 2005 09:44:37

Модель шифратора.

Через Х={x} - множество всех открытых текстов.

Через У={y} - множество всех закрытых текстов.

Через К={k} - множество всех ключей.

(отображает множество открытых текстов в множество шифр текстов) – алгоритм, который шифрует:

- в зависимости от ключа преобразование различное – множество всех преобразований;

- множество всех шифр текстов, которые получены при шифровании всех открытых текстов на ключе k.

Правила расшифровки будем обозначать - отображение всего множества шифртекстов на ключе k в X:

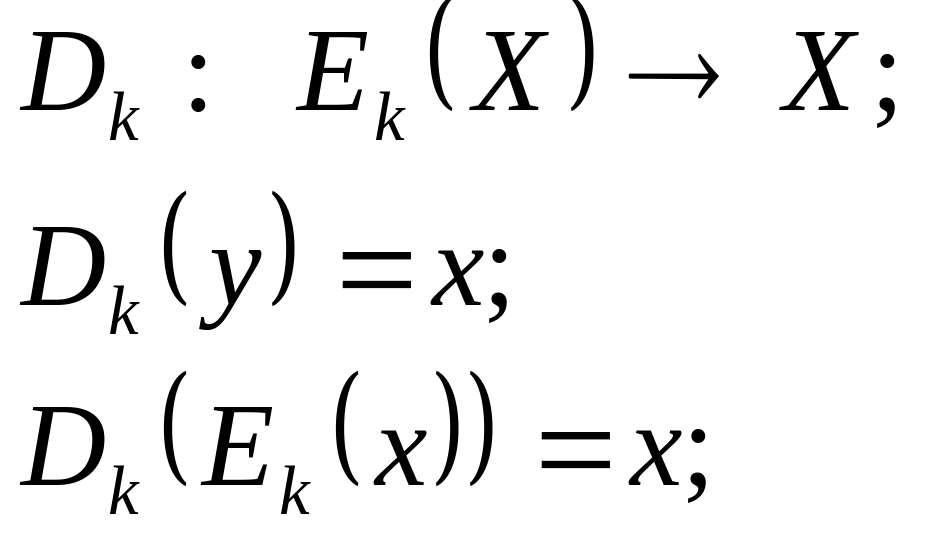
- множество всех алгоритмов расшифровки.

Определения:

Шифром ( шифром системы) назовём совокупность , удовлетворяющих соотношению.

1) Для любых и выполняется - однозначность расшифровки;

2) - множество шифр текстов это только оно и других быть не может , принадлежит .

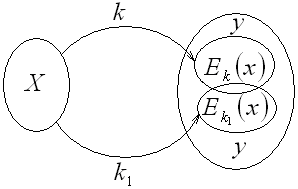
Верно ли:

Итого неверно, а верно когда .

То есть при , при этом k никогда y не получится.

Из первого следует свойство иньективности - алгебраическая модель:

.

Доказательство от противного:

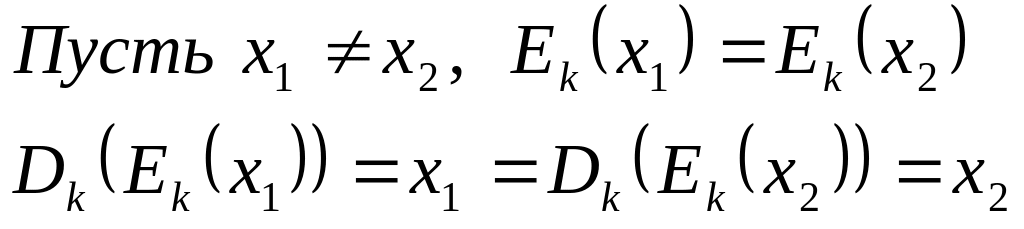
Пришли к противоречию: чтд.

Введём понятие вероятностной модели. На практике распределение может быть равномерным.

Введём распределение:

Под вероятностной моделью шифра будем понимать модель, состоящую из 7 множеств:

Алфавит:

A – строим открытый текст.

В - строим шифр текст.

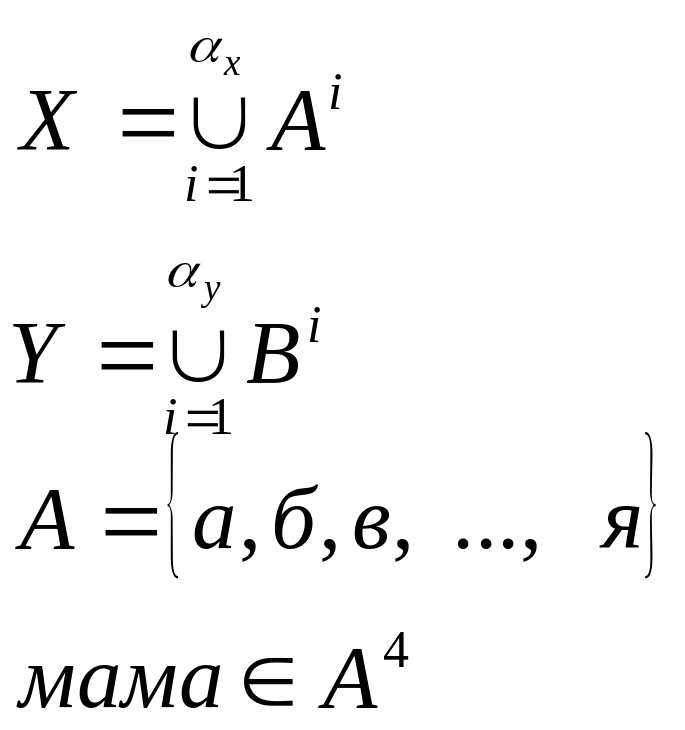
подстановка – таблица

Состоит из одних и тех же элементов и при этом не повторяются.

На этом множестве заданны какие-то операции

Пример:

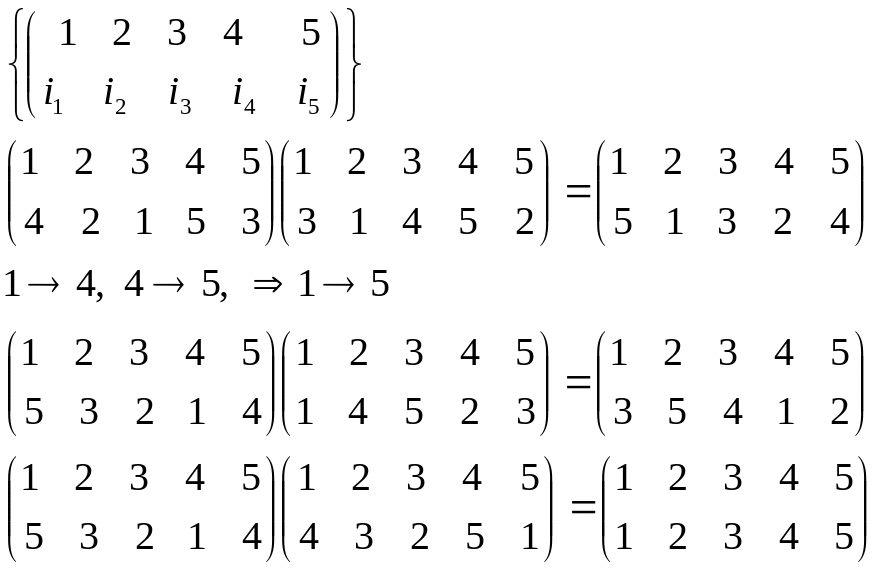
Такое множество называется симметрической группой.

Определения некоторых конкретных шифров.

Определение шифра замены:

- конечное множество;

- множество подстановок.

Симметрическая группа – заменяем элемент индексом;

Пусть у нас множества Х и Y - совпадают: K является подмножеством S(A).

Тогда шифром замены наматывается преобразование, когда:

Для любого , и любого , и любого .

Правила шифрования и расшифровки определяется формулой:

- какая-то буква которая при… переходит в букву

Букву заменяем на другую букву из этого алфавита.

- тождественная подстановка.

Пример:

Чт, сен 22 2005 09:31:49

Определение шифра перестановки.

Если буквы открытого текста при шифровании лишь меняются местами друг с другом, то мы имеем дело с шифром перестановки.

Пусть А - алфавит

, А – декартово произведение, множество последовательностей длинны L.

S(L) – некоторая симметрическая граница на множестве {1, ..., L} K подмножество S(L)

Шифром перестановки называется шифр:

Для любого , и любого .

Правила шифрования и дешифрования определяются формулой:

Из выбора конкретного k следует выбор конкретной перестановки.

Пример: