§ 6. Нормальная форма Фробениуса.

Пусть — произвольное поле, а

- многочлен ненулевой степени над полем . Матрица

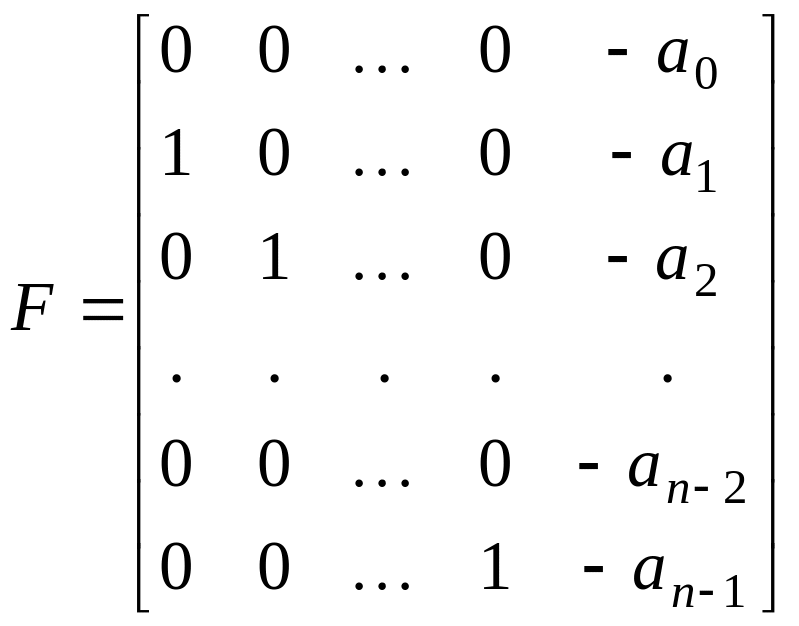
называется клеткой Фробениуса, сопровождающей многочлен . Например,

-

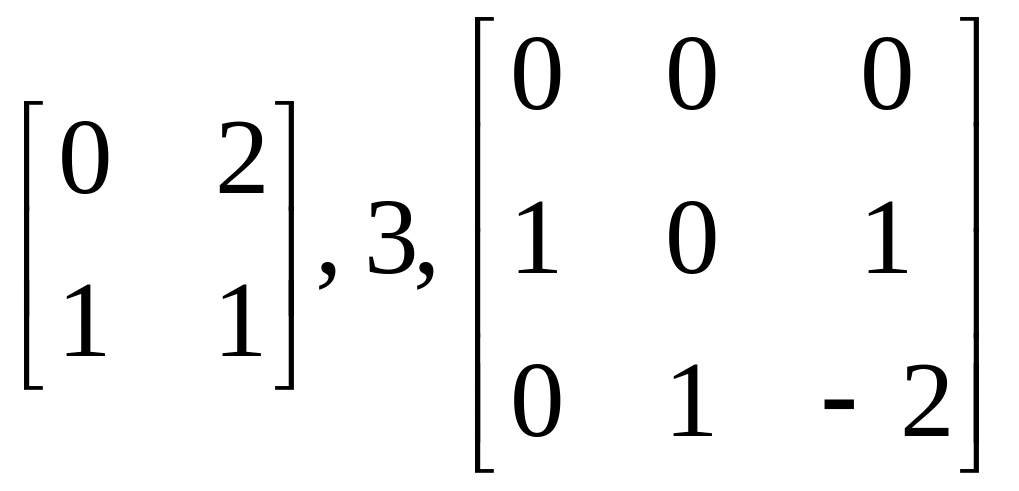клетки Фробениуса, сопровождающие соответственно многочлены . Пусть

(I)

такая система многочленов ненулевых степеней над полем , что для многочлен делит многочлен и старший коэффициент каждого из них равен I. Пусть, далее, - клетка

Фробениуса, сопровождающая многочлен .

Квазидиагональная матрица называется матрицей Фробениуса, сопровождающей систему многочленов (I).

Если — матрица, а — подобная ей матрица Фробениуса, то называется нормальной формой Фробениуса матрицы .

Пусть — клетка Фробениуса, сопровождающая многочлен - расширение поля , содержащее все корни многочлена и — каноническое разложение многочлена над полем . Разлагая определитель

по элементам последнего столбца, получим . Вычислим количество клеток Жордана с диагональным элементом в жордановой нормальной форме матрицы , . С этой целью вычислим вначале ранг матрицы .

.

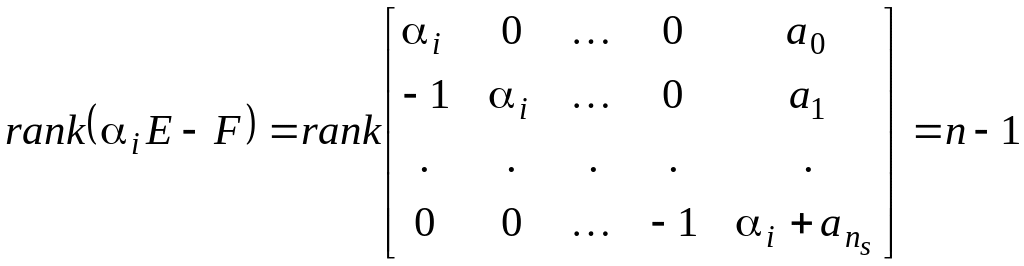Следовательно, , и, значит, матрица

является жордановой нормальной формой матрицы над полем . Поэтому минимальный многочлен клетки Фробениуса равен и, значит, минимальный многочлен матрицы Фробениуса, сопровождающей систему многочленов (1), равен .

Пусть теперь — произвольная матрица над полем , — расширение поля , содержащее все корни характеристического многочлена матрицы ,

(2)

есть система ее элементарных делителей над полем . Будем считать многочлены в системе (2) расположенными так, что

(3)

Пусть для определенности, первая цепочка неравенств (3) самая длинная, т.е. . Введя обозначения , получим неравенства

(4)

Рассмотрим многочлены

(5)

Заметим, что равен НОК системы (2).

Упражнение. По аналогии с доказательством леммы I § 5 можно доказать, что коэффициенты многочленов принадлежат полю . Докажите.

В силу неравенств (4) для каждого многочлен делит многочлен . Пусть — матрица Фробениуса, сопровождающая систему многочленов (5) . В силу того, что система элементарных делителей квазидиагональной матрицы является объединением систем элементарных делителей ее клеток, и только что рассмотренного случая, когда — клетка Фробениуса, системы элементарных делителей матриц и совпадают. Следовательно, матрицы и подобны над полем , — нормальная форма Фробениуса матрицы .

Упражнение. Доказать, что матрицы и подобны над полем . (Для решения этого упражнения можно использовать идею доказательства леммы 4 § 5.)

Докажем единственность нормальной формы Фробениуса матрицы . Пусть еще нормальная форма Фробениуса матрицы и сопровождает систему многочленов . Тогда подобна . Поэтому минимальные многочлены матриц и равны, т.е. . Следовательно, и, значит, системы элементарных делителей матриц и совпадают. Поэтому эти матрицы подобны. Проводя индукцию по числу , теперь получаем и . Учитывая , получаем .