5. Расчет показателей эффективности смо с ожиданиями

Постановка задачи:

В систему, состоящую из n каналов, поступает входящий поток заявок с интенсивностью ᴧ (или tср). Заявки обслуживаются любым свободным каналом с интенсивностью обслуживания μ (или tобсл). В случае занятости всех каналов, заявка становятся в очередь и ожидают освобождения любого канала.

Необходимо определить все критерии эффективности работы СМО с ожиданиями.

Список используемых терминов и обозначений:

1) Количество каналов: N

2) Интенсивность входящего потока заявок: λ

3) Интенсивность обслуживания заявок: μ

4) Приведенная интенсивность потока заявок: α

5) Вероятность того, что СМО свободна и может обслужить заявку: Pо

6) Вероятность того, что СМО занята, а в очереди нет заявок: рк

7) Вероятности того, что СМО занята, а в очереди находятся

1,2,...,m заявок: рn+r

8) Абсолютная пропускная способность СМО: A

9) Вероятность того, что заявка будет немедленно обслужена: Pн.обсл

10) Вероятность того, что заявка получит отказ: Pож

11) Среднее число заявок, стоящих в очереди: rcp

12) Среднее число занятых каналов: ʓ

13) Среднее время ожидания заявки в очереди: tож

Формулы для расчетов:

2) Λ=

3) μ=

4) α= λ*tобсл = = =

5) po=

6) pk=

7) pn+r= * * po

8) А=ᴧ

9) Pн.обсл=1- * * po

10) Pож= * * po

11) rcp=Pож*

12) ᶚk=α

13) tож=rср*tср

6. Примеры Пример решения задачи смо с отказами.

Задача:

В частную телефонную справочную службу поступает 11 заявок в час. Среднее время обслуживания одной заявки составляет 0,15 часа. Каждая обслуженная заявка приносит доход 130 руб. а содержание одного оператора обходится в 122 руб. в час.

Найти оптимальное количество операторов справочной службы, чтобы доход был максимальным.

Математическая постановка задачи:

На вход многоканальной СМО с отказами поступает поток заявок, интенсивность которого составляет 11 заявок/час. Среднее время обслуживания одной заявки 0,15 часа.

Каждая заявка приносит доход 130 руб., а содержание одного канала обходится в 122 руб./час.

Найти оптимальное число каналов СМО.

Решение:

Воспользовавшись данными из условия задачи и обозначениями, принятыми в пункте 5, проведем следующие вычисления:

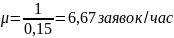
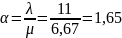
Из условия задачи также вытекает, что в случае, если СМО имеет n каналов, то она приносит доход D = D(n) , который можно определить по формуле.

Где A=A(n) – абсолютная пропускная способность СМО

В случае, когда каналов n=1, получаем:

Вероятность отказа в обслуживании заявки:

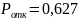
Вероятность немедленного обслуживания заявки:

Абсолютная пропускная способность СМО:

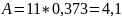
Считаем прибыль:

Вывод: при наличии 1-го канала обслуживания, доход будет равен 411р.

Аналогично рассчитываем прибыль для другого количества каналов:

При n=2

,

11*0,66=7,26

Вывод: при наличии 2-ух каналов обслуживания, доход будет равен 699р.

При n=3

Вывод: при наличии 3-ех каналов обслуживания, доход будет равен 835,2р.

При n=4

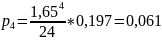
Вывод: при наличии 4-ех каналов обслуживания, доход будет равен 854,77р.

При n=5

Вывод: при наличии 5-ти каналов обслуживания, доход будет равен 734,2р.

Сравнивая доходы, поступающие от СМО в случаях n =1,2,3,4,5, замечаем, что при увеличении числа каналов от одного до четырех доход растет и при n = 4 становится наибольшим. Это значение и является оптимальным.

Ответ. Оптимальным является наличие 4-х операторов справочной службы. В этом случае доход предприятия будет максимальным.

Пример решения задачи СМО с ожиданиями.

Задача:

В службу технической поддержки поступают звонки с интенсивностью 81 в час. Средняя продолжительность обслуживания заявки 2 минуты. В случае занятости всех операторов, звонок переводится в режим ожидания обслуживания.

Определить минимальное количество операторов службы тех-поддержки, при котором очередь ожидающих звонков не будет расти до бесконечности.

Математическая постановка задачи:

В СМО с ожиданиями поступает поток заявок с интенсивностью   чел. в час. Средняя продолжительность обслуживания одной заявки    мин.

Определить минимальное количество каналов обслуживания  , при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при  

Решение:

По условию   (1/ч)   (1/мин.).

По формуле

.

Очередь не будет возрастать до бесконечности при условии , т.е. при . Таким образом, минимальное количество операторов n=3.

Найдем характеристики обслуживания СМО при n=3.

Вероятность того, что звонков нет, определяем по формуле:

т.е. в среднем 2,5% времени операторы будут свободны.

Вероятность занятости каждого оператора:

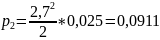
Вероятность того, что звонки будут переведены в режим удержания, определяем по формуле:

Вероятность того, что абонент будет обслужен немедленно:

Среднее число заявок в очереди:

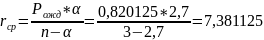
Среднее время ожидания заявки в очереди:

Среднее число занятых каналов:

ʓк=α

ʓк=2,7

Ответ: Минимально необходимое количество телефонных операторов, чтобы очередь звонков не росла до бесконечности, равно 3.