2. Соединения на врубках

Врубкой называется соединение элементов деревянных конструкций, в которых передача усилия от одного элемента к другому осуществляется путем плотного соприкасания примыкающих плоскостей.

На рис. 8.10 показан пример лобовой врубки с одним зубом.

Верхний, сжатый элемент упирается в специально устроенное гнездо в нижнем, растянутом. Скалывание дерева происходит вдоль волокон по площадке .

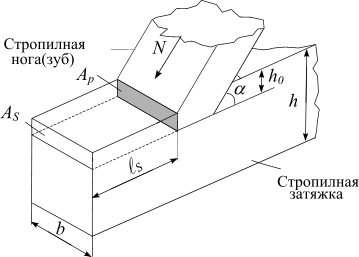
Рис. 8.10

Условие прочности на скалывание:

(8.20)

где – длина площадки скалывания. Требуемую длину находят из условия (8.20).

Смятие древесины происходит по площадке .

Условие прочности на смятие:

(8.21)

где – глубина врубки, которую находят из условия (8.21).

При расчетах надо иметь в виду, что древесина, будучи материалом анизотропным, по–разному сопротивляется одним и тем же силовым воздействиям в зависимости от их направления по отношению к волокнам.

2. Кручение

8.2.1. Основные понятия

Кручение – вид нагружения бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент, обозначаемый или .

Деформация кручения возникает при нагружении бруса парами сил, плоскости действия которых перпендикулярны его продольной оси. Моменты этих пар будем называть скручивающими моментами и обозначать m (рис. 8.11).

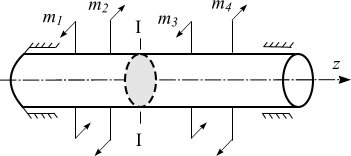
Рис. 8.11

Брус, работающий на кручение, называется валом.

Кручению подвергаются валы двигателей, станков и машин, оси моторных вагонов и локомотивов, элементы пространственных конструкций.

При расчете вала внешние скручивающие моменты могут быть выражены через мощность и угловую скорость (из курса ТМ) по формулам

или , (8.22)

где [Н.м] – внешний скручивающий момент; [Вт]– мощность; [рад/с] – угловая скорость; – число об/мин.

Если вал находится в состоянии покоя или равномерного вращения, то алгебраическая сумма всех скручивающих моментов равна нулю (рис. 8.11):

. (8.23)

Задачи определения напряжений и деформаций при кручении методами СМ могут быть решены только для брусьев с круглыми сечениями, для брусьев с некруглыми сечениями такие задачи решаются методами теории упругости.

2. Вычисление крутящих моментов. Построение эпюр

Если вал нагружен только двумя моментами, то из условия равновесия эти моменты всегда равны по величине и направлены в противоположные стороны (рис. 8.12 а). В других случаях крутящий момент определяют методом сечений. Вал рассекают плоскостью, мысленно отбрасывают одну часть, а ее действие на оставшуюся часть заменяют неизвестным крутящим моментом (рис. 8.12 б). Составляют уравнение равновесия для оставшейся левой части :

, ,

из которого и определяют значение момента:

. (8.24)

Крутящий момент, возникающий в произвольном сечении вала, численно равен алгебраической сумме внешних скручивающих моментов, приложенных к оставленной части.

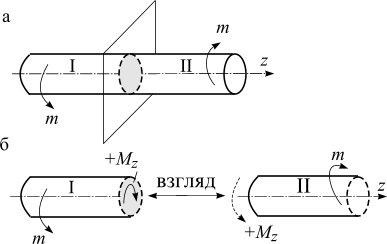
Рис. 8.12

Правило знаков:

Условимся считать крутящий момент положительным, если внешний момент направлен против часовой стрелки при взгляде от сечения к любому концу вала. Тогда положительный крутящий момент (M_z) изображается по часовой стрелке (рис. 8.12 б).

Например, для вала (рис. 8.12) крутящий момент в сечении I–I из равновесия:

– левой части ;

– правой части .

Оба эти значения равны между собой. Это видно из равенства (8.23).

Заметим, что принятое правило знаков не имеет физического смысла. Оно необходимо при построении эпюр. Положительные значения будем откладывать вверх от базиса, отрицательные – вниз.

Иногда на вал действует распределенная моментная нагрузка интенсивности (рис. 8.13 а).

Вырежем малый элемент (рис. 8.13 б).

Рис. 8.13

б

а

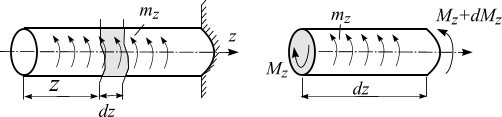
Действие левой и правой отброшенной части вала заменим крутящим моментом, причем справа он имеет приращение . Составим уравнение равновесия:

, ,

Откуда

. (8.25)

Производная крутящего момента по абсциссе сечения равна интенсивности распределенной моментной нагрузки.

Пример 8.1. Построить эпюру крутящих моментов для вала (рис. 8.14 а).

Скручивающие моменты изображены в виде двух кружочков: кружочек с точкой обозначает силу, направленную на наблюдателя, а кружочек с крестиком - силу от наблюдателя.