1.8. Моделі факторного аналізу: детерміновані (функціональні), стохастичні (імовірнісні)
У основі економічного аналізу лежать виявлення, оцінка і прогнозування впливу факторів на зміну результативних показників. Повною мірою ця теза відноситься до будь-якого розділу економічного аналізу, тобто і до фінансового аналізу. Функціонування будь-якої соціально-економічної системи здійснюється в умовах складної взаємодії комплексу факторів внутрішнього і зовнішнього порядку. Чинник - причина, рушійна сила якого-небудь процесу або явища, що визначає його характер або одну з основних рис. Всі чинники, що впливають на систему і визначають її поведінку, знаходяться у взаємозв'язку і взаємозумовленості. Зв'язок економічних явищ - сумісна зміна двох або більшої кількості явищ. Серед багатьох форм закономірних зв'язків явищ важливу роль виконує причинна, суть якої полягає в породженні одного явища іншим. Такі зв'язки називаються детермінованими, або причинно-наслідковими.
Кількісна характеристика взаємозв'язаних явищ здійснюється за допомогою ознак (показників). Ознаки, що характеризують причину, називаються факторними (незалежними, екзогенними); ознаки, що характеризують наслідок, називаються результативними (залежними, ендогенними). Сукупність факторних і результативних ознак, зв'язаних одним причинно-наслідковим зв'язком, називається факторною системою.
Модель факторної системи - це математична формула, що виражає реальні зв'язки між аналізованими явищами; у найзагальнішому вигляді вона може бути записана так:
у = f(Х1, Х2, ..., Хn),
де у - результативна ознака;
хi – факторні ознаки.
Процес побудови аналітичного виразу залежності називається процесом моделювання явища, що вивчається. Існують два типи зв'язків, які піддаються дослідженню в процесі факторного аналізу: функціональні і стохастичні.
Зв'язок називається функціональним, або жорстко детермінованим, якщо кожному значенню факторної ознаки відповідає цілком певне невипадкове значення результативної ознаки. Як приклад можна навести залежності, реалізовані в межах відомої моделі факторного аналізу фірми «Дюпон». Зв'язок називається стохастичним (вірогідним), якщо кожному значенню факторної ознаки відповідає безліч значень результативної ознаки, тобто певний статистичний розподіл. Прикладом такої залежності можуть служити регресійні рівняння, вживані, наприклад, при розрахунку бета-коефіцієнтів для аналізу портфельних інвестицій.
Можна навести і іншу інтерпретацію розглянутих зв'язків з позиції поведінки системи, що описує деяке явище і кількісно характеризується сукупністю показників. Система називається жорстко детермінованою, якщо за заданих початкових умов вона переходить в єдиний, визначений стан; система називається вірогідною, якщо за одних і тих же початкових умов вона може переходити в різні стани, що мають різну вірогідність.
Розглянуті зв'язки можуть бути прямими і зворотними. У першому випадку зростання (зменшення) факторної ознаки спричиняє зростання (зменшення) результативної ознаки. У другому випадку зростання (зменшення) факторної ознаки спричиняє за собою зменшення (зростання) результативної ознаки.
При вивченні зв'язків у фінансовому аналізі розв'язується декілька задач:
встановлення факту наявності або відсутності зв'язку між аналізованими показниками;
вимірювання тісноти зв'язку;
встановлення невипадкового характеру виявлених зв'язків;
кількісна оцінка впливу зміни факторів на зміну результативного показника;
виділення найважливіших факторів, що визначають поведінку результативного показника.
Залежно від виду аналізу ці задачі розв'язуються за допомогою різних прийомів: жорстко детерміновані зв'язки - балансовий метод, прийом ланцюгових підстановок, інтегральний метод та ін.; стохастичні зв'язки - кореляційний аналіз, коваріаційний аналіз, метод головних компонент і ін.
У найзагальнішому вигляді система факторного аналізу може бути представлена таким чином (рис. 1.8.).
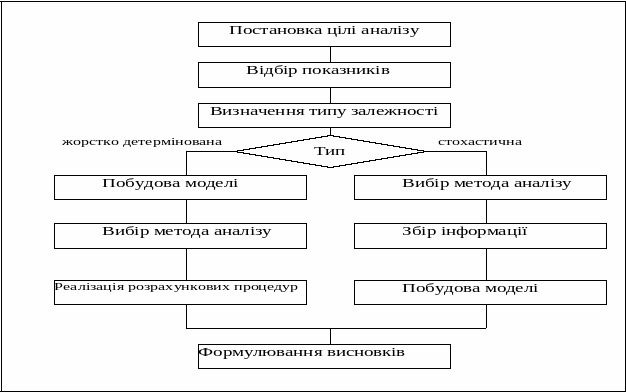Рис.1.8.
Узагальнена схема факторного аналізу
Жорстко детерміновані моделі факторного аналізу.
Ці моделі набули достатньо широкого розповсюдження в межах традиційного ретроспективного аналізу: Аналіз за допомогою жорстко детермінованих факторних моделей, який іноді скорочено називають детермінованим аналізом, має низку особливостей.
По-перше, при детермінованому підході факторна модель повністю замикається на ту систему фактора, які піддаються об'єднанню в дану модель. Межею складання такої моделі є довжина безперервного ланцюга прямих зв'язків.
По-друге, даний підхід не дозволяє розділити результати впливу факторів, які діють одночасно і не піддаються об'єднанню в одній моделі. Таким чином, дослідник умовно абстрагується від дії інших факторів, а всі зміни результативного показника повністю приписуються впливу факторів, включених в модель.
По-третє, детермінований аналіз може виконуватися для одиничного об'єкту у відсутність сукупності спостережень.
Існують наступні види моделей детермінованого аналізу:
аддитивна модель, тобто модель, в яку фактори входять у вигляді алгебраїчної суми; як приклад можна навести відому модель товарного балансу:
Р = Зн + Н - Зк - В,
де Р - реалізація;
Зн - запаси на початок періоду;
Н - надходження товарів;
Зк - запаси на кінець періоду;
В - інше вибуття товарів;
мультиплікативна модель, тобто модель, в яку фактори входять у вигляді добутку; як приклад можна навести просту двофакторну модель:
Р = Ч • ПП,
де Р - реалізація;
Ч - чисельність;
ПП - продуктивність праці;
кратна модель, тобто модель, що є відношенням факторів:
де Фо - фондоозброєність;
ОЗ - вартість основних засобів;
Ч - чисельність;
змішана модель, тобто модель, в яку фактори входять в різних комбінаціях:
де Р - реалізація;
Рт - рентабельність;
ОЗ - вартість основних засобів;
Об - вартість оборотних коштів.
Жорстко детермінована модель, що має більше двох факторів називається багатофакторною. Аналізуються такі моделі за допомогою різних прийомів.
Детермінований факторний аналіз має достатньо жорстку послідовність виконуваних процедур:
побудова економічно обґрунтованої (з позиції факторного аналізу) детермінованої факторні моделі;
вибір прийому факторного аналізу підготовка умов для його виконання;
реалізація рахункових процедур аналізу моделі, включаючи перевірку;
формулювання висновків і рекомендацій за наслідками аналізу.
Перший етап виключно важливий, оскільки неправильно побудована модель може привести до логічно невиправданих і неправильних результатів. Зміст даного етапу полягає в наступному: будь-яке розширення жорстко детермінованої факторної моделі не повинне суперечити логіці зв'язку «причина - наслідок». Розглянемо простий приклад моделі, що зв'язує обсяг реалізації (Р), чисельність (Ч) і виробіток (ПП). Теоретично можна досліджувати три моделі:
Р = Ч • ПП; Ч = Р / ПП; ПП = Р / Ч;
З позиції арифметики всі представлені формули бездоганні, проте з позиції факторного аналізу тільки перша має сенс, оскільки саме в ній показники, що стоять в правій частині формули, є факторами, тобто причиною, що породжує і визначає значення показника, що стоїть в лівій частині (наслідок).
На другому етапі вибирається один з прийомів аналізу фактора: інтегральний, ланцюгових підстановок, логарифмічний і ін. Найпоширенішим є метод ланцюгових підстановок (або його наслідок - прийом арифметичних різниць), що має, проте, один вельми істотний недолік - залежно від вибраного порядку заміни факторів їх розкладання можуть бути різні. Ця проблема має насправді виключно теоретичне значення, що ж до її практичної значущості, зокрема стосовно ретроспективного аналізу, то вона мізерна - важливі тенденції і відносна значущість того або іншого фактора, а не «точні» оцінки їх впливу. Проте, для дотримання деякого більш менш універсального підходу до визначення порядку заміни факторів в моделі можна сформулювати низку рекомендацій.
Перш за все, потрібно відзначити, що не існує і не може існувати у принципі єдиної формалізованої методики визначення цього порядку - існує безліч моделей, в яких він може бути встановлений чисто волюнтаристським шляхом. Лише для невеликого числа моделей можна використовувати деякі формалізовані підходи. Введемо ряд визначень.
Ознака, що безпосередньо відноситься до явища, яка вивчається, і характеризує його кількісний бік, називається первинною або кількісною. Це ознаки: а) абсолютні (об’ємні); б) їх можна підсумовувати у просторі та часі. Приклад: обсяг реалізації, чисельність працівників, вартість оборотних коштів.
Ознаки, що відносяться до явища, яке вивчається, не безпосередньо, а через одну або декілька інших ознак і характеризують якісний бік явища, що вивчається, називаються вторинними, або якісними. Це ознаки: а) відносні; б) їх не можна підсумовувати у просторі та часі. Приклад: виробіток, фондовоозброєність, рентабельність і т.п. В аналізі виділяють вторинні фактори 1-го, 2-го і т.д. порядку, одержувані шляхом послідовної деталізації.
Жорстко детермінована факторна модель називається повною, якщо результативний показник кількісний, і неповної, якщо результативний показник якісний. У повній двох факторні моделі один фактор завжди кількісний, другий - якісний. В цьому випадку, як це прийнято у вітчизняній статистиці, заміну фактора рекомендують починати з кількісного показника.
Достатньо широке розповсюдження в аналізі фактора мають багатофакторні мультиплікативні моделі (БММ). Можна сформулювати деякі правила побудови таких моделей.
1. БММ повинна бути економічно обґрунтована, тобто місце фактора в моделі повинне відповідати його економічній ролі у формуванні результативної ознаки.
2. БММ доцільно будувати з повної двофакторної моделі шляхом послідовного розкладання факторів (як правило, якісних) на складові; при черговому розширенні моделі необхідно ретельно стежити за дотриманням зв'язку «причина - наслідок».
3. БММ повинна бути такою, щоб фактори можна було укрупнювати (згортка моделі) і зліва направо, і справа наліво, а добуток двох будь-яких факторів, що стоять поряд, давав би економічно зрозумілий фактор вищого порядку.
4. Побудову неповної БММ в більшості випадків рекомендується починати з побудови і подальшої деталізації відповідної повної моделі.
5. При написанні формули БММ фактори в моделі рекомендується розташовувати у порядку їх заміни зліва направо.
Стохастичне моделювання є певною мірою доповненням і поглибленням детермінованого факторного аналізу. У факторному аналізі ці моделі використовуються з трьох основних причин:
необхідно вивчити вплив факторів, по яких не можна побудувати жорстко детерміновану факторна модель (наприклад, рівень фінансового левериджу);
необхідно вивчити вплив факторів, які не піддаються об'єднанню в одній і тій же жорстко детермінованій моделі;
необхідно вивчити вплив складних факторів, які не можуть бути виражені одним кількісним показником (наприклад, рівень науково-технічного прогресу).
На відміну від жорстко детермінованого стохастичний підхід для реалізації вимагає низку передумов:
а) наявність сукупності;
б) достатній обсяг спостережень - в економічних дослідженнях нерідко доводиться працювати в умовах малих вибірок (до 20 спостережень). Нерідко як об'єкт аналізу використовують всю наявну сукупність; в цьому випадку прийнято розглядати її як вибірку з гіпотетичної сукупності, що складається зі всіх можливих у принципі значень модельованих показників. Оскільки стохастична модель - це, як правило, рівняння регресії, вважається, що кількість спостережень повинна як мінімум в 6-8 разів перевищувати кількість факторів;
в) випадковість і незалежність спостережень. Це вимога найважча для виконання, оскільки однією з особливостей економічних показників є їх інерційність і взаємозалежність. Нерідко цією вимогою нехтують або відсівають взаємно корелюючі ознаки за допомогою спеціальних статистичних методів;
г) однорідність. Якісна однорідність досягається шляхом логічного відбору; критерієм кількісної однорідності може служити, зокрема, коефіцієнт варіації - його значення не повинне перевищувати 33%;
д) наявність розподілу ознак, близького до нормального. Існують різні статистичні методи перевірки нормальності розподілу. Виконання цієї вимоги в економічних дослідженнях нерідко зв'язане з істотними труднощами і не завжди можливе;
е) наявність спеціального математичного апарату. Залежно від умов, в яких проводиться аналіз, можуть застосовуватися різні методи: регресійний аналіз, коваріаційний аналіз, спектральний аналіз і ін.
Побудова стохастичної моделі проводиться у декілька етапів:
якісний аналіз (постановка мети аналізу, визначення сукупності, визначення результативних і факторних ознак, вибір періоду, за який проводиться аналіз, вибір методу аналізу);
попередній аналіз модельованої сукупності (перевірка однорідності сукупності, виключення аномальних спостережень, уточнення необхідного обсягу вибірки, встановлення законів розподілу показників, що вивчаються);
побудова стохастичної (регресійної) моделі (уточнення переліку факторів, розрахунок оцінок параметрів рівнянь регресії, перебір конкуруючих варіантів моделей);
оцінка адекватності моделі, перевірка статистичної істотності рівняння в цілому і його окремих параметрів, перевірка відповідності формальних властивостей оцінок завданням дослідження;
економічна інтерпретація і практичне використання моделі.
ТЕМА 2. ІНФОРМАЦІЙНЕ ЗАБЕЗПЕЧЕННЯ ФІНАНСОВОГО АНАЛІЗУ ТА ЗАГАЛЬНА ОЦІНКА ФІНАНСОВОГО СТАНУ
2.1. Класифікація вхідної аналітичної інформації. Джерела інформації, вимоги до неї
2.2. Баланс як основна форма фінансової звітності
2.3. Побудова аналітичних балансів
2.4. Експрес-аналіз бухгалтерської звітності
2.5. Аналіз валюти бухгалтерського балансу
2.6. Горизонтальний і вертикальний аналіз балансу