
- •Техническое задание
- •1.1 Цель курсового проектирования
- •Технические требования к объекту
- •1.3 Исходные данные для проектирования
- •2 Техническое предложение
- •2.1 Выбор материала
- •2.2 Конструктивно силовая схема агрегата
- •2.2.1 Лонжеронно-балочный фюзеляж
- •2.2.2 Балочно-обшивочный фюзеляж
- •2.2.3 Балочно-стрингерный фюзеляж
- •2.3 Элементы конструкции отсека хвостовой части фюзеляжа
- •2.3.1 Шаг продольного и поперечного набора элементов
- •2.3.2 Обшивка
- •2.3.3 Стрингеры
- •2.3.4 Шпангоуты
- •Нормальные шпангоуты
- •Усиленные шпангоуты
- •Гермошпангоут
- •2.4 Соединение элементов каркаса и обшивки
- •2.5 Технологические и эксплуатационные разъемы фюзеляжа
- •2.6 Конструкция пола хвостового отсека фюзеляжа самолета
- •2.7 Узлы крепления к фюзеляжу отдельных агрегатов
- •2.8 Конструктивные особенности герметических кабин
- •Эскизный проект
- •Раскрой листов обшивки
- •Толщина обшивки и размеры стрингера
- •Определение размеров нормального шпангоута
- •Определение размеров силового шпангоута
- •4.3.1 Определение внутренних силовых факторов
- •4.3.2 Определение размеров поперечного сечения
- •Проверочный расчет ригеля хвостового отсека фюзеляжа
- •4.4.1 Определение внутренних силовых факторов
- •4.4.2 Определение поперечного сечения ригеля
- •4.4.3 Построение эпюры напряжений
- •4.4.4 Определение прогиба
- •Моделирование ригеля в среде femap v10.2
- •4.5.1 Построение модели
- •4.5.2 Задание свойств материала
- •4.5.3 Задание свойств конечных элементов
- •Список литературы
4.3.2 Определение размеров поперечного сечения
После
определения реакций опор, определяем
значения внутренних силовых факторов.
Для этого используем метод сечений. В
поперечном сечении шпангоута при
нагружении возникают три внутренних
силовых фактора – продольная сила
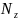 ,
поперечная сила
и изгибающий момент
,
поперечная сила
и изгибающий момент
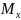 .
.
Ось шпангоута является окружностью,
следовательно, положение произвольного
сечения зададим в полярной системе
координат через радиус кривизны
и угол поворота сечения
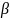 .
Тогда, внутренние силовые факторы будут
функциями угла
–
.
Тогда, внутренние силовые факторы будут
функциями угла
–
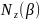 ,
,
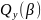 ,
,
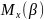 .
.
Продольная сила
в рассматриваемом сечении численно
равна алгебраической сумме проекций
всех внешних сил, взятых по одну сторону
от сечения, на ось
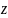 ,
направленную по нормали к данному
сечению (Рисунок Ч).
,
направленную по нормали к данному
сечению (Рисунок Ч).
Поперечная сила
в рассматриваемом сечении численно
равна алгебраической сумме проекций
всех внешних сил, взятых по одну сторону
от сечения, на ось
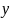 ,
лежащую в плоскости сечения и
перпендикулярно оси шпангоута (Рисунок
Ч).
,
лежащую в плоскости сечения и
перпендикулярно оси шпангоута (Рисунок
Ч).
Изгибающий
момент
в рассматриваемом сечении численно
равен алгебраической сумме моментов
всех внешних сил, взятых по одну сторону
от сечения, относительно оси
 ,
лежащей в плоскости перпендикулярно
плоскости кривизны шпангоута (Рисунок
Ч, ось
проецируется
в точку).
,
лежащей в плоскости перпендикулярно
плоскости кривизны шпангоута (Рисунок
Ч, ось
проецируется
в точку).
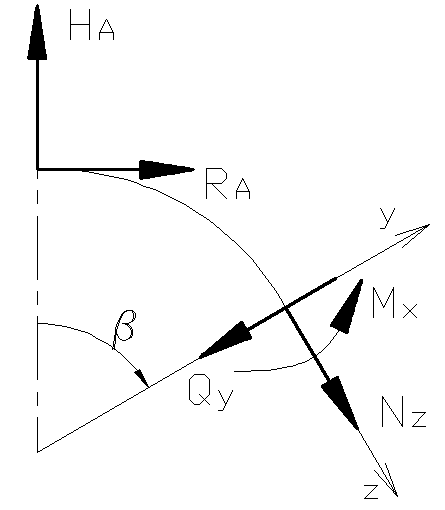
Рисунок Ч - ппп
Рассмотрим
первый участок шпангоута, имеющий
координату
 .
По сечению производим мысленный разрез
и отбрасываем и отбрасываем часть
шпангоута. Действие отброшенной части
шпаноута на оставшуюся заменятся
внутренними силовыми факторами
,
,
.
Для оставшейся части составляются
уравнения равновесия.
.
По сечению производим мысленный разрез
и отбрасываем и отбрасываем часть
шпангоута. Действие отброшенной части
шпаноута на оставшуюся заменятся
внутренними силовыми факторами
,
,
.
Для оставшейся части составляются
уравнения равновесия.
Для
удобства определения
и
в сечении с координатой
,
реакции и силы раскладываются на
составляющие, параллельные осям
 и
этого произвольного сечения.
и
этого произвольного сечения.
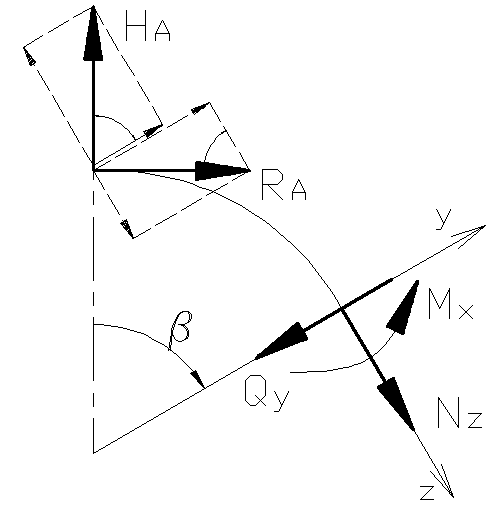
Рисунок
Продольная
сила определится как проекция реакций
и
 на ось
:
на ось
:
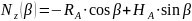 ;
;
Поперечная сила определится как проекция реакций и на ось
:
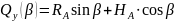 ;
;
Изгибающий момент определится как момент реакций относительно оси х:
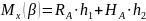 ;
;
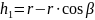 ;
;
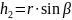 ;
;
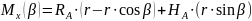 .
.
Рассмотрим
второй участок шпангоута, имеющий
координату
 .
.
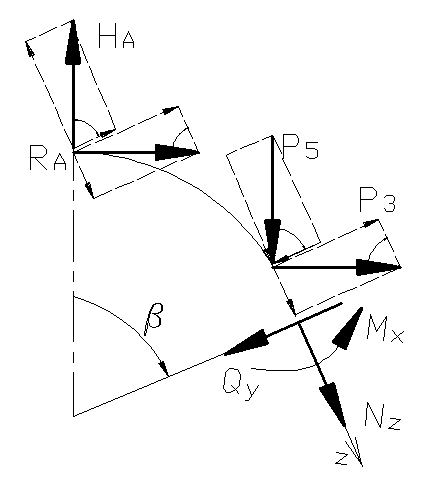
Рисунок
Продольная сила определится как проекции сил на ось :
 ;
;
Поперечная сила определится как проекция сил на ось :
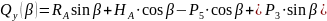 ;
;
Изгибающий момент определится как момент сил относительно оси х:
;
;
;
.
Рассмотрим
третий участок шпангоута, имеющий
координату
 .
.
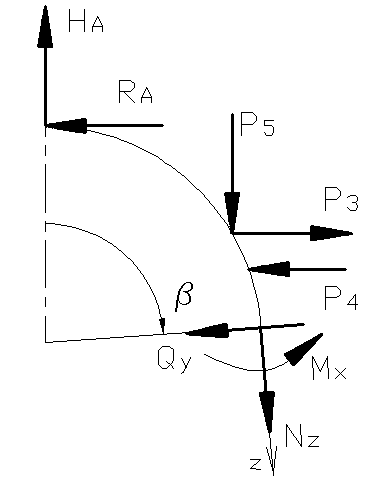
Рисунок
Продольная сила определится как проекции сил на ось :
 ;
;
Поперечная сила определится как проекция сил на ось :
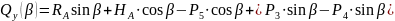 ;
;
Изгибающий момент определится как момент сил относительно оси х:
;
;
;
.
Для построения эпюр определяются значения , , в характерных сечениях. Для удобства данные сведены в таблицу Я.+
Таблица 6 – Значения внутренних силовых факторов в сечениях.
β, 0 |
0 |
60 |
65 |
70 |
90 |
180 |
, кН |
|
|
|
|
|
|
, кН |
|
|
|
|
|
|
, кНм |
|
|
|
|
|
|
Исходя из рекомендаций взятых из учебной литературы (ЛизинВ.Т.стр.338) зададимся формой и соотношением геометрических параметров сечения. В качестве сечения силового шпангоута примем профиль двутаврового сечения. Зададимся следующими зависимостями геометрических параметров сечения:
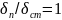 ;
;
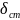 /
=0.02;
/
=0.02;
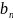 =0,5
,
=0,5
,
где
 - толщина полки; мм;
- толщина полки; мм;
- толщина стенки; мм;
- высота стенки; мм;
– ширина полки; мм.
Момент инерции сечения шпангоута равен
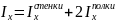 ,
,
где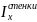 - момент инерции сечения стенки; м4;
- момент инерции сечения стенки; м4;
 - момент инерции сечения полки; м4.
- момент инерции сечения полки; м4.
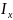 =
·
=
·
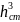 /
/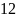 +
+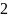 [
·
[
·
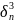 /12+(
/12+(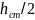 +
+
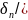 2)2·
2)2·
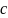 ·
δп]
·
δп]
Подставляя соотношения в
формулу получим, что
=0,05649
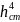 .
.
Запишем формулу момента сопротивления и подставим в нее найденный момент инерции
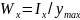 ,
,
где
 – момент сопротивления
сечения шпангоута; м3;
– момент сопротивления
сечения шпангоута; м3;
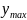 – максимальное
расстояние сечения от нейтральной оси;
м.
– максимальное
расстояние сечения от нейтральной оси;
м.
=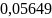 /(
+
)=
/(
+
)= .
.
Запишем условие прочности:
≥
 ,
,
Где
 - максимальный изгибающий момент; кН·м;
- максимальный изгибающий момент; кН·м;
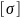 - допускаемое напряжение; МПа.
- допускаемое напряжение; МПа.
Подставим в формулу значения, указанные в исходных данных
≥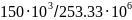 =
=
=
≥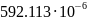
Отсюда
 .
.
Окончательные размеры поперечного сечения силового шпангоута:
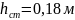 ;
=
;
=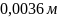 ;
=
;
;
=
;
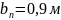 .
.
Сечение силового шпангоута показано на рисунке 23.
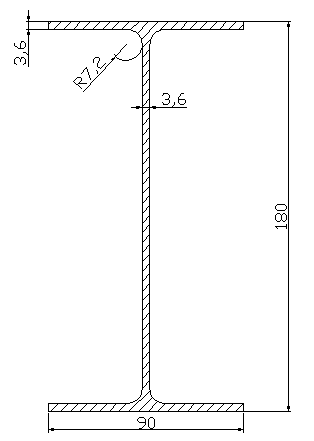
Рисунок 23 – Поперечное сечение силового шпангоута
Геометрические характеристики остальных силовых шпангоутов приведены в таблице 6.
Таблица 6 – Геометрические параметры силовых шпангоутов
Номер сечения |
, м |
, м |
, м |
, м |
4 |
0,18 |
0,9 |
0,0036 |
0,0036 |
8 |
0,16 |
0,8 |
0,0032 |
0,0032 |
11 |
0,12 |
0,6 |
0,0024 |
0,0024 |
