7.3 Способы задания конечных автоматов

Определение конечного автомата как пятерки объектов с детальным описанием функции переходов слишком громоздко и неинформативно.

Существуют два более удобных способа описания автоматов:

1. таблица переходов

2. диаграмма (граф) переходов

Таблица переходов: строки отмечены состояниями, а столбцы - входными символами. Начальное состояние находится всегда в первой строке, в конечные состояния – отмечены символом *.

Составим таблицу переходов КА из примера 1.

	a	b
q0	{ q1}	{ q0}
q1	{ q1}	{ q2}
q2	{ q3}	{ q0}
q3*	{ q3}	{ q3}

Диаграммой переходов НКА называется неупорядоченный граф, удовлетворяющий следующим условиям:

• каждому состоянию q соответствует некоторая вершина, отмеченная его именем;

• диаграмма переходов содержит дугу из состояния p в состояние q, отмеченную символом a, если р   (q, a). Если существуют несколько входных символов, переводящих автомат из состояния p в состояние q, то диаграмма переходов может содержать дугу, отмеченную списком этих символов

• вершины, соответствующие заключительным состояниям, отмечаются двойным кружком, остальные состояния – одинарным.

На рисунке приведен граф переходов конечного автомата из примера 1:

b

a

a

q₀

q₁

a, b

b

b

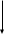
a

q₃

q₂

8. Контекстно-свободные грамматики и языки

К классу контекстно-свободных грамматик (КС) относятся грамматики, у которых не накладывается никаких ограничений на вид правых частей их правил, а левая часть каждого правила – единственный нетерминал. С помощью КС-грамматик задаются синтаксис языков программирования.

Напомним, что все правила КС-грамматики имеют вид: А, где А  N,   ТN. КС-грамматики служат для определения КС-языков и их регулярных подмножеств.

1. Проверка существования языка

Проверка существования языка выполняется перед всеми другими исследованиями и преобразованиями КС-грамматики. Алгоритм проверки основан на вычислении множества нетерминалов, порождающих терминальные строки. Если начальный символ грамматики оказывается среди этих нетерминалов, то язык, определяемый грамматикой не пуст, т.е. существует.

Обозначим N= {Z | ZN, Z*x, xT} и рассмотрим алгоритм проверки существования языка.

Вход: КС-грамматика G=(N, T, P, S)

1. Положить N₀=

2. Вычислить N₁= N₀  {A | (A)  P и   (N₀  T)*}

3. Если N₁ N₀ , то положить N₀= N₁ и перейти к п.2; иначе положить N= N₁

4. Если SN, то язык существует, иначе язык не существует

Пример. Язык, определяемый грамматикой с правилами

1) S AB 2) A  aA 3) A  a 4) B  b

не пуст, что подтверждает результат применения изложенного алгоритма.

1. N₀=

2. N₁={A, B}

3. N₁= N₀ ? Нет N₀ = N₁={A, B}

4. N₁={A, B, S}

5. N₁= N₀ ? Нет N₀ = N₁={A, B, S}

6. N₁={A, B, S}

7. N₁= N₀ ? Да N = N₁={A, B, S}

5. SN то L(G) =, т.е. язык существует