
- •Теория функций комплексного переменного Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Вариант № 9
- •Вариант № 10
- •Вариант № 11
- •Вариант № 12
- •Вариант № 13
- •Вариант № 14
- •Вариант № 15
- •Вариант № 16
- •Вариант № 17
- •Вариант № 18
- •Вариант № 19
- •Вариант № 20
- •Вариант № 21
- •Вариант № 22
- •Вариант № 23
- •Вариант № 24
- •Вариант № 25
- •Вариант № 26
- •Вариант № 27
- •Вариант № 28
- •Вариант № 29
- •Вариант № 30
________________________________________________________________________________
Теория функций комплексного переменного Вариант № 1
Вычертить область, заданную неравенствами
![]() .
.
Доказать аналитичность функции
![]()
и найти ее производную.
Восстановить аналитическую в окрестности точки z = 0 функцию f(z) по известной мнимой части
![]()
и
значению
![]() .
.
Вычислить интеграл
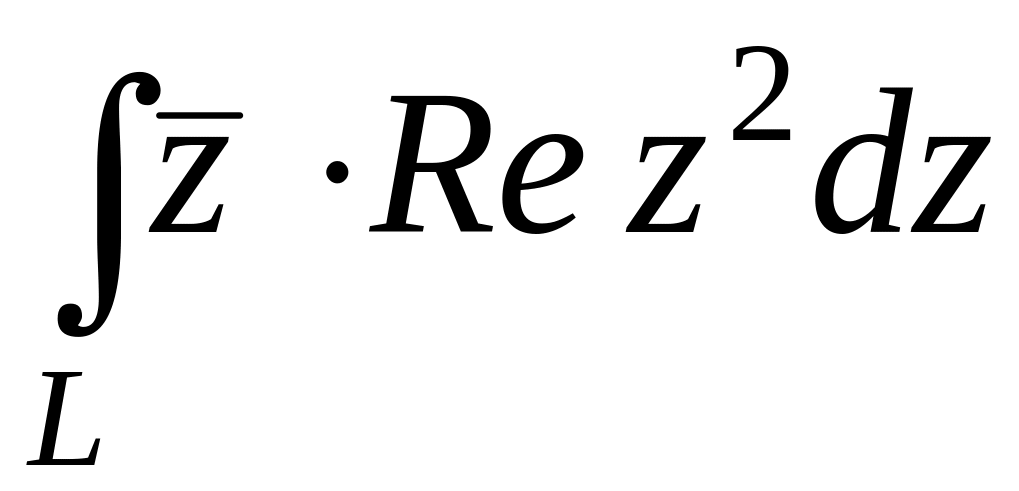 ,
,
где
L
– отрезок прямой, соединяющий точки
![]() и
и
![]() .
.
Используя интегральную формулу Коши, вычислить интеграл:
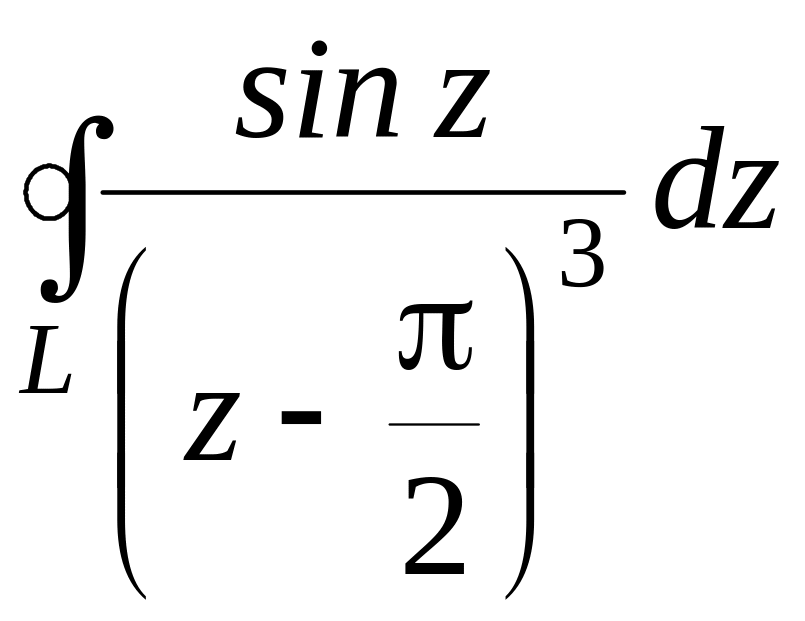 ,
L
:
,
L
:
![]()
Используя теорему о вычетах, вычислить интеграл:
![]() ,
L:
,
L:
![]() .
.
Найти все лорановские разложения функции
![]() по
степеням
по
степеням
![]() .
.
Вариант № 2
Вычертить область, заданную неравенствами
![]() .
.
Доказать аналитичность функции
![]()
и найти ее производную.
Восстановить аналитическую в окрестности точки z=0 функцию f(z) по известной действительной части
![]()
и значению .
Вычислить интеграл
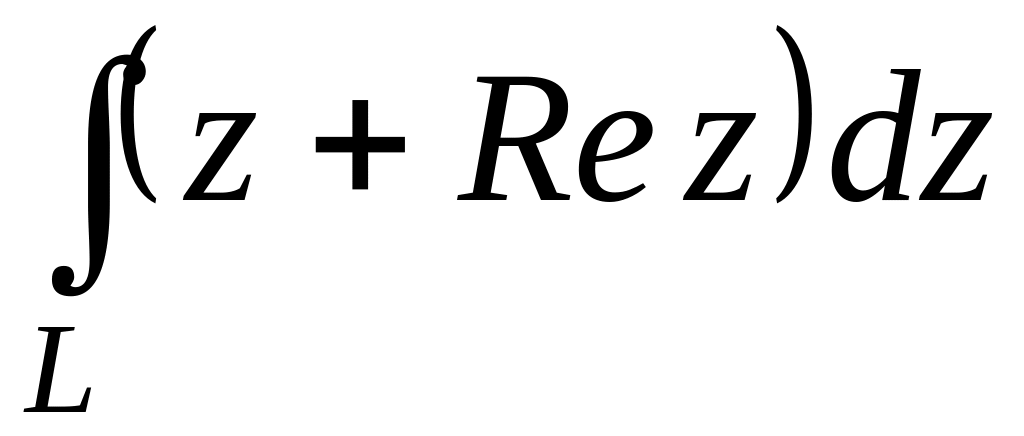 ,
,
где
L
– дуга параболы
![]() от точки
от точки
![]() до точки
до точки
![]()
Используя интегральную формулу Коши, вычислить интеграл:
![]() ,
L:
,
L:
![]()
Используя теорему о вычетах, вычислить интеграл:
![]() ,
L:
,
L:
![]() .
.
Найти все лорановские разложения функции
по
степеням
![]() .
.
Вариант № 3
Вычертить область, заданную неравенствами
![]()
Доказать аналитичность функции
![]()
и найти ее производную.
Восстановить аналитическую в окрестности точки z=0 функцию f(z) по известной мнимой части
![]()
и
значению
![]() .
.
Вычислить интеграл
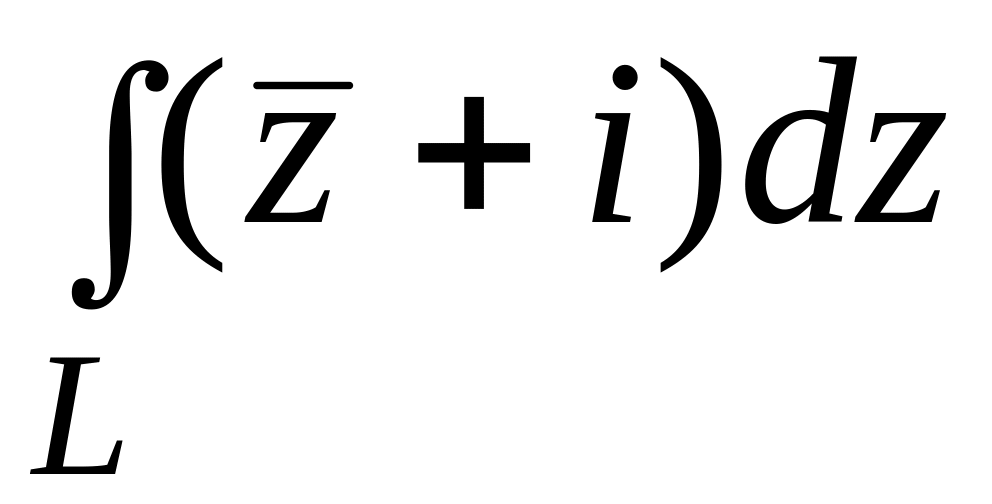 ,
,
где
L
– дуга параболы
![]() от точки
от точки
![]() до точки
до точки
![]() .
.
Используя интегральную формулу Коши, вычислить интеграл:
![]() ,
L
:
,
L
:
![]()
Используя теорему о вычетах, вычислить интеграл:
![]() ,
L:
,
L:
![]() .
.
Найти все лорановские разложения функции
по
степеням
![]() .
.
Вариант № 4
Вычертить область, заданную неравенствами
![]() .
.
Доказать аналитичность функции
![]()
и найти ее производную.
Восстановить аналитическую в окрестности точки z=0 функцию f(z) по известной действительной части
![]()
и значению .
Вычислить интеграл
 ,
,
где
L
– отрезок прямой, соединяющий точки
![]() .
.
Используя интегральную формулу Коши, вычислить интеграл:
![]() .
.
Используя теорему о вычетах, вычислить интеграл:
![]() ,
L:
,
L:
![]() .
.
Найти все лорановские разложения функции
![]() в
окрестности точки
в
окрестности точки
![]() .
.
Вариант № 5
Вычертить область, заданную неравенствами
![]() .
.
Доказать аналитичность функции
![]()
и найти ее производную.
Восстановить аналитическую в окрестности точки z=1 функцию f(z) по известной мнимой части
![]()
и
значению
![]() .
.
Вычислить интеграл
 ,
где L
– дуга параболы
,
где L
– дуга параболы
 от точки
от точки
 до точки
до точки
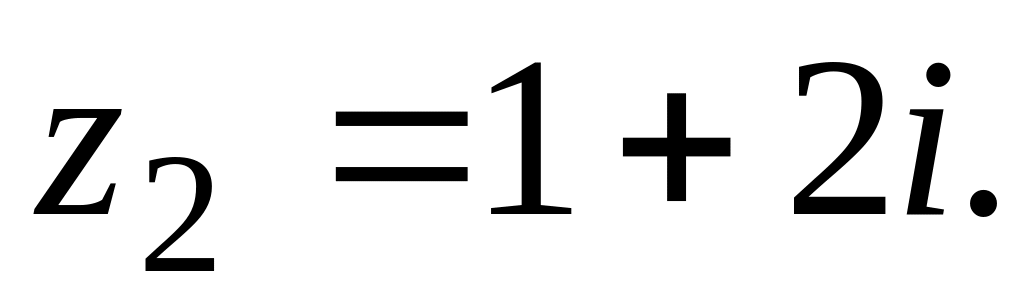
Используя интегральную формулу Коши, вычислить интеграл:
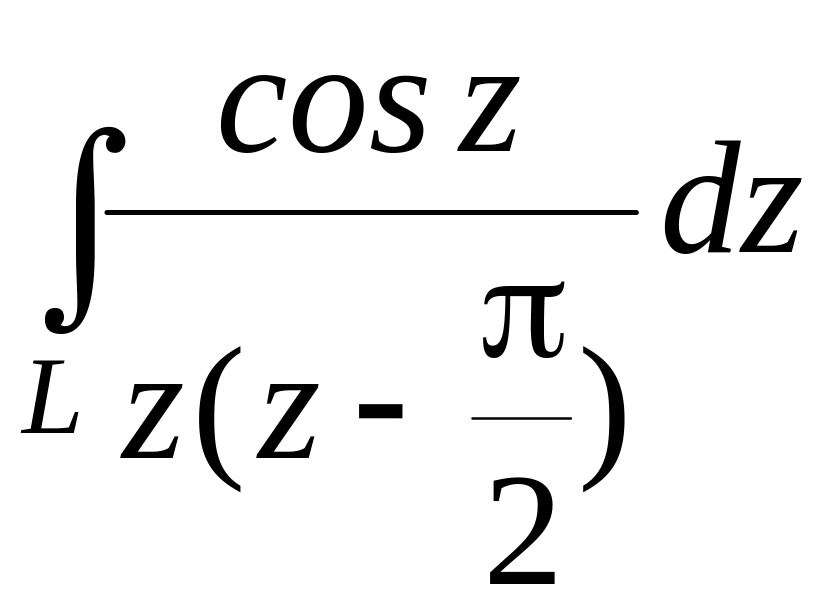 ,
L:
,
L:
Используя теорему о вычетах, вычислить интеграл:
![]() ,
L:
,
L:
![]() .
.
Найти все лорановские разложения функции
![]() по
степеням
по
степеням
![]() .
.
