1.2.7. Закон сохранения энергии

В системе тел, между которыми действуют только консервативные силы, полная механическая энергия не изменяется со временем.

Т + П = Е = const. (1.39)

1.2.8. Удар абсолютно упругих и неупругих тел

Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остаeтся никаких деформаций, и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.

В случае взаимодействия двух тел

; (1.40)

. (1.41)

Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.

В случае взаимодействия двух тел

. (1.42)

1.2.9. Момент инерции

Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

. (1.43)

Для цилиндра или диска радиусом R .

Для прямого тонкого стержня длиной L для оси, перпендикулярной стержню и проходящей через его середину

.

Теорема Штейнера. Момент инерции тела I относительно любой оси вращения равен моменту его инерции I_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния a между осями:

I = I_c + ma². (1.44)

1.2.10. Кинетическая энергия вращения

Кинетическая энергия вращающегося тела

(1.45)

где I_z – момент инерции тела относительно оси вращения; ω - угловая скорость.

1.2.11. Закон всемирного тяготения

Закон всемирного тяготения. Между любыми двумя телами действует сила взаимного притяжения:

, (1.46)

где m₁, m₂ – массы тел; r – расстояние между телами; G – гравитационная постоянная.

Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения. На тело массой m, внесённое в это поле, действует сила F = m g .

Поле тяготения является потенциальным, а силы, действующие в нем, консервативными.

Работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус:

A = -ΔП = - (П₂-П₁) = П₁ - П₂. (1.47)

1.3. Механика жидкостей

1.3.1. Давление в жидкости и газе

Давлением p называется физическая величина, определяемая нормальной силой, действующей со стороны жидкости или газа на единицу площади

(1.48)

.

1.3.2. Закон Архимеда

Закон Архимеда. На тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом жидкости или газа: F_A = ρ g V, (1.49)

где ρ – плотность жидкости (газа); V – объём погружённого тела.

1.3.3. Уравнение неразрывности

П роизведением скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока (рис. 10):

S₁U₁ = S₂U₂ = const. (1.50)

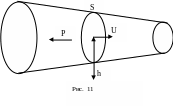
1.3.4. Уравнение Бернулли

, (1.51)

где 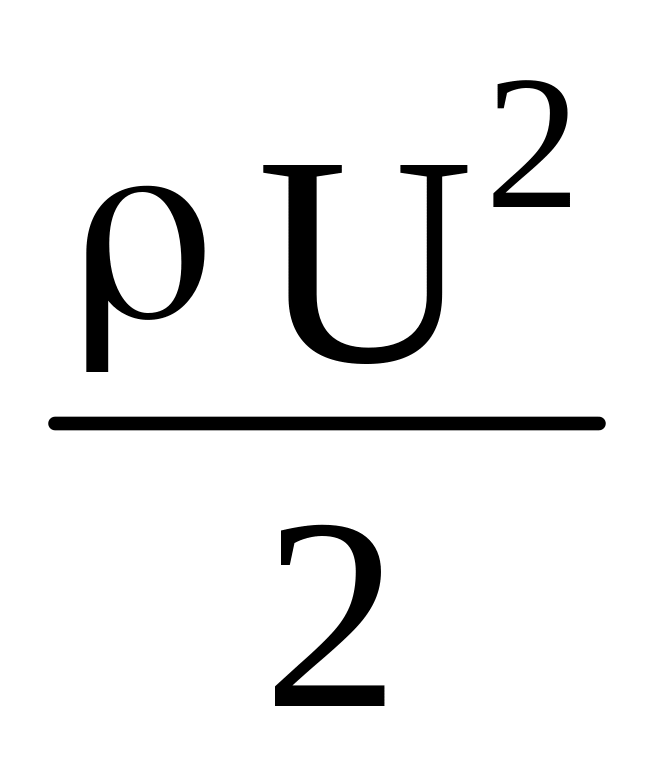– динамическое давление; ρ g h – гидростатическое давление; р – статическое давление.

1.3.5. Вязкость

Вязкость (внутреннее трение) – это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.

При перемещении одних слоев жидкости относительно других возникает силы внутреннего трения.

(1.52)

где η – коэффициент пропорциональности, называемый вязкостью; – градиент скорости, показывает, как меняется скорость от слоя к слою; S – рассматриваемая площадь поверхности слоя.

Ламинарным называется течение жидкости, если вдоль потока один слой скользит относительно другого, не перемешиваясь.

Турбулентным называется течение жидкости, если вдоль потока происходит вихреобразования и перемешивания жидкости.

Характер течения зависит от безразмерной величины, называемой числом Рейнольдса:

(1.53)

где – кинематическая вязкость; d – диаметр трубы; – средняя по сечению трубы скорость жидкости.

При Re <1000 имеет место ламинарное течении жидкости; при Re = 2300 – турбулентное течение жидкости.