1 Механика

Лекция 1

Физические основы механики

План лекции 1

1.1. Элементы кинематики

1.1.1.Система отсчета

1.1.2. Скорость

1.1.3. Ускорение и его составляющие

1.1.4. Угловая скорость и угловое ускорение

1.2. Динамика

1.2.1. Законы Ньютона

1.2.2. Сила трения

1.2.3. Закон сохранения импульса

1.2.4. Центр масс

1.2.5. Работа и энергия

1.2.6 Кинетическая и потенциальная энергия

1.2.7. Закон сохранения энергии

1.2.8. Удар абсолютно упругих и неупругих тел

1.2.9. Момент инерции

1.2.10. Кинетическая энергия вращения

1.2.11. Закон всемирного тяготения

1.3. Механика жидкостей

1.3.1. Давление в жидкости и газе

1.3.2. Закон Архимеда

1.3.3. Уравнение неразрывности

1.3.4. Уравнение Бернулли

1.3.5. Вязкость

1.5.6. Метод Стокса

1.1. Элементы кинематики

1.1.1. Система отсчета

В декартовой системе координат положение точки А в данный момент времени определяется тремя координатами x, y, z или радиусом-вектором , проведенным из начала системы координат в данную точку (рис. 1).

Движение точки А описывается скалярными уравнениями

(1.1)

эквивалентными векторному уравнению . (1.2)

1.1.2. Скорость

Векторная величина скорость определяет быстроту движения и его направление в данный момент времени (рис. 2).

З десь ∆ S – путь; – перемещение

Вектор средней скорости равен (1.3)

М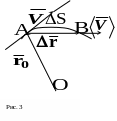 гновенная скорость (1.4)

Мгновенная скорость равна первой производной радиуса-вектора по времени. Модуль мгновенной скорости

При Δt → 0 Δr → ΔS.

Средняя скорость неравномерного движения (1.5)

Из выражения ds = U dt получим длину пути, пройденного точкой за промежуток времени от t₁ до t₂

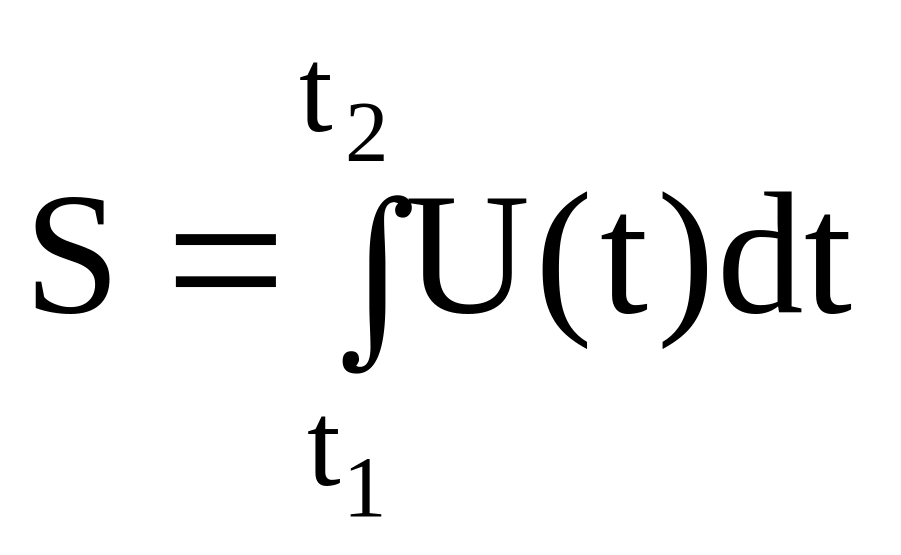. (1.6)

1.1.3. Ускорение и его составляющие

Рассмотрим плоское движение (рис. 4).

Перенесем вектор в точку А и найдем .

С реднее ускорение . (1.7)

Мгновенное ускорение (1.8)

Мгновенное ускорение равно первой производной скорости по времени.

Разложим вектор на две составляющие: и .

Т ангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю:

(1.9)

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории (рис. 5).

. (1.10)

Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих:

(1.11)