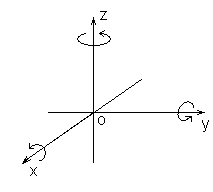753 Задача ¹ 3
Возьмем полоску бумаги, согнем ее пополам К раз следующим образом:
и развернем полоску так, чтобы углы на всех сгибах стали равны 90 .
Посмотрев на торец полоски, увидим ломаную, которая называется
"драконовой ломаной К-го порядка":
К=0 К=1 К=2 К=3
Написать алгоритм, который, получая на входе числа K и L, рисует
драконову ломаную К-го порядка с длиной одного звена, равной L.
ПРАКТИЧЕСКИЙ ТУР.
1 вариант
754 Задача ¹ 1
Дан список всех 64 полей шахматной доски 8 х 8 в виде числовых
координат. Написать алгоритм, который определяет, является ли этот
список маршрутом ферзя по всем полям доски.
755 Задача ¹ 2
Дана упорядоченная по возрастанию линейная таблица натуральных
чисел А[1] <...< A[N]. Найти наименьшее натуральное число, не
представимое в виде суммы некоторых чисел из таблицы. Сумма может
состоять и из одного слагаемого; каждый элемент таблицы может входить
в нее не более одного раза. Приемлемое решение должно укладываться в
С*N действий, где С - постоянная, не зависящая от N.
2 вариант
756 Задача ¹ 1
Составить алгоритм, получающий на входе число K и выдающий на
выходе К-тое по порядку четырехзначное число, у которого никакие две
цифры не равны между собой. Первым таким числом является 0123.
757 Задача ¹ 2
Имеются две таблицы натуральных чисел А[1:N] и B[1:N]. Найти
перестановку i[1], i[2],..., i[N] чисел 1, 2,...,N, для которой сумма
A[1] * B[i[1]] + ... +A[N] * B[i[N]] минимальна. В перестановку
каждое число должно входить только один раз. Достаточно эффективным
будет считаться алгоритм, требующий выполнения К * N операций, где К
- постоянная величина, не зависящая от N. Наилучшее известное решение
требует выполнения К*N*Log N операций.
758 Т.9.1.
Есть N контактов. Проводами соединены контакты: 1-й со 2-м, 2-й с
3-м, 3-й с 4-м,...,N-1-й с N-м.
._______._____._____. . . . .________.
1 2 3 4 N-1 N
В нескольких проводах случился обрыв. Составить алгоритм,
выясняющий за наименьшее количество проб, в каких проводах случился
обрыв. Одна проба проверяет, идет ли ток между i-м и k-м контактами.
Алгоритм при пробе может пользоваться вспомогательным литерным
алгоритмом - функцией ЕСТЬТОК(i,k),принимающей значения "Да" или
"Нет".
759 Т.9.2.
Дана функция, аргументы которой - произвольные натуральные числа
f(M-N,N), при М>N
f(M,N)= N, при М=N
f(N-M,M), при N>M
Составить алгоритм, вычисляющий значение функции без помощи
рекурсии.
760 Т.9.3.
Есть N селений. Некоторые селения попарно соединены тропинками,
вне селений никакие две тропинки общих точек не имеют. В
целочисленной таблице ТРОПЫ[1:N, 1:N] задана информация о тропинках;
количество тропинок между i-тым и j-тым селениями равно значению
элемента таблицы ТРОПЫ[i,j]=ТРОПЫ[j,i] (в том числе для i=j) Написать
алгоритм, определяющий, можно ли нарисовать карту тропинок, не
отрывая карандаша от бумаги и не рисуя ни одну тропу дважды.
10 класс
Теоретический тур
761 Т.10.1.
Написать алгоритм, отгадывающий число N, задуманное человеком,
задавая ему "да-нет" вопросы. N может быть любым конечным натуральным
числом. Алгоритм должен использовать как можно меньше вопросов при
больших N. Для диалога с человеком используются вспомогательные
алгоритмы ВВОД и ВЫВОД с любым количеством параметров любых типов.
762 Т.10.2.
Данa функция, аргументы которой - неотрицательные целые числа M и
N (M £ N)
1, при М=0
f(M,N)=f(M-1,N-1)+f(M,N-1), при 0 < М < N
1, при M=N
Составить алгоритм, вычисляющий значение функции без помощи
рекурсии.
763 Т.10.3.
Набор обобщенного домино состоит из М костей, на каждой кости
нанесены два целых числа от 0 до N; любая пара чисел может
встречаться в наборе 0, 1 или несколько раз. Значения костей заданы в
таблице ДОМИНО[1:M,1:2]. Составить алгоритм, определяющий, можно ли
построить из всех костей набора цепь по правилам домино.
П р а к т и ч е с к и й т у р .
764 Два человека играют в такую игру: есть электрическая схема, в
которую входят батарейка, лампочки и контакты, к которым можно
присоединять любое количество проводов.
Игроки ходят по очереди: при каждом ходе игрок соединяет проводом
любую пару различных контактов, которая ранее не была соединена
напрямую каким-либо игроком. Игрок, после хода которого будут гореть
все лампочки, считается выигравшим.
Написать программу, выступающую за одного из игроков и стремящуюся
к выигрышу. Сопротивление всех проводов считать равным 0.
Теоретический тур.
765 Т10.1 Одинокий король долго бродил по бесконечной шахматной доске.
Известна последовательность из n его ходов (вверх, вниз, влево,
вправо, вверх-влево и т.п.) Составить алгоритм, определяющий, побывал
ли король дважды на одном и том же поле за минимальное возможное при
заданном n количество вычислений.
766 Т10.2 Задан массив чисел A[1:N, 1:M], упорядоченный по убыванию по
строкам и столбцам т.е.:
A[I,1] ? A[I,2] ? ... ? A[I,M] (при всех I)
A[1,J] ? A[2,J] ? ... ? A[N,J] (при всех J)
Найти элемент массива, равный заданному числу и напечатать его
индексы (I,J). Напечатать слово "нет", если такого элемента не
окажется. Решение необходимо найти за k*(M+N), а не за k*(M*N)
операций, где k - константа, не зависящая от N и M.
767 Т10.3 Заданы N2 чисел {1,2,...,N2 (N>2). Составить алгоритм,
который расположит эти числа в N групп так, что одновременно будут
выполняться следующие условия:
1) Каждая группа содержит N чисел
2) Каждое число принадлежит только одной группе
3) Суммы чисел во всех группах одинаковы.
11 класс.
768 Теоретический тур.
Т11.1 Даны 3 литерные переменные S1, S2, S3. Составить алгоритм,
который в переменной S1 заменяет все подстроки, равные S2, на
подстроки, равные S3. Замены должны проводится слева направо;
очередная замена выполняется на подстроке, в которой уже выполнены
предыдущие замены.
769 Т11.2 Задан массив чисел A[1:N, 1:M, 1:L], упорядоченный по
убыванию по каждому измерению, т.е.:
A[I,J,1] ? A[I,J,2] ? ... ? A[I,J,L] (при всех I,J)
A[I,1,K] ? A[I,2,K] ? ... ? A[I,M,K] (при всех I,K)
A[1,J,K] ? A[2,J,K] ? ... ? A[N,J,K] (при всех J,K).
Найти элемент массива, равный заданному числу и напечатать его
индексы (I,J,K). Напечатать слово "нет", если такого элемента не
окажется. Решение необходимо найти за C*L*(M+N), а не за C*L*(M*N)
операций, где C - константа, не зависящая от N,M и K.
770 T11.3 Составить алгоритм, определяющий последовательность
выполнения N работ, если для каждой работы задан список работ,
результаты которых она должна непосредственно использовать: этот
список может быть пустым. Напечатать соответствующее сообщение, если
последовательность работ нельзя определить. Наилучший алгоритм
определяет порядок за K*(D+N) операций, где D - размер всех списков;
K - константа, не зависящая от N и D.
10-11 класс.
771 Практический тур.
Составить и реализовать на ЭВМ программу, распознающую
шестизначный почтовый индекс за наименьшее количество запросов. При
одном запросе программа должна указывать человеку требуемый отрезок
сетки и получать ответ, входит ли он в состав изображения цифры.
Теоретический тур.
772 Т10.1 Одинокий король долго бродил по бесконечной шахматной доске.
Известна последовательность из n его ходов (вверх, вниз, влево,
вправо, вверх-влево и т.п.) Составить алгоритм, определяющий, побывал
ли король дважды на одном и том же поле за минимальное возможное при
заданном n количество вычислений.
773 Т10.2 Задан массив чисел A[1:N, 1:M], упорядоченный по убыванию по
строкам и столбцам т.е.:
A[I,1] ? A[I,2] ? ... ? A[I,M] (при всех I)
A[1,J] ? A[2,J] ? ... ? A[N,J] (при всех J)
Найти элемент массива, равный заданному числу и напечатать его
индексы (I,J). Напечатать слово "нет", если такого элемента не
окажется. Решение необходимо найти за k*(M+N), а не за k*(M*N)
операций, где k - константа, не зависящая от N и M.
774 Т10.3 Заданы N2 чисел {1,2,...,N2 (N>2). Составить алгоритм,
который расположит эти числа в N групп так, что одновременно будут
выполняться следующие условия:
1) Каждая группа содержит N чисел
2) Каждое число принадлежит только одной группе
3) Суммы чисел во всех группах одинаковы.
11 класс.
775 Теоретический тур.
Т11.1 Даны 3 литерные переменные S1, S2, S3. Составить алгоритм,
который в переменной S1 заменяет все подстроки, равные S2, на
подстроки, равные S3. Замены должны проводится слева направо;
очередная замена выполняется на подстроке, в которой уже выполнены
предыдущие замены.
776 Т11.2 Задан массив чисел A[1:N, 1:M, 1:L], упорядоченный по
убыванию по каждому измерению, т.е.:
A[I,J,1] ? A[I,J,2] ? ... ? A[I,J,L] (при всех I,J)
A[I,1,K] ? A[I,2,K] ? ... ? A[I,M,K] (при всех I,K)
A[1,J,K] ? A[2,J,K] ? ... ? A[N,J,K] (при всех J,K).
Найти элемент массива, равный заданному числу и напечатать его
индексы (I,J,K). Напечатать слово "нет", если такого элемента не
окажется. Решение необходимо найти за C*L*(M+N), а не за C*L*(M*N)
операций, где C - константа, не зависящая от N,M и K.
777 T11.3 Составить алгоритм, определяющий последовательность
выполнения N работ, если для каждой работы задан список работ,
результаты которых она должна непосредственно использовать: этот
список может быть пустым. Напечатать соответствующее сообщение, если
последовательность работ нельзя определить. Наилучший алгоритм
определяет порядок за K*(D+N) операций, где D - размер всех списков;
K - константа, не зависящая от N и D.
10-11 класс.
778 Практический тур.
Составить и реализовать на ЭВМ программу, распознающую
шестизначный почтовый индекс за наименьшее количество запросов. При
одном запросе программа должна указывать человеку требуемый отрезок
сетки и получать ответ, входит ли он в состав изображения цифры.
ТЕОРЕТИЧЕСКИЙ ТУР
779 1. Многоугольник задан координатами вершин (x1,y1), (x2,y2),...,
(xn,yn), перечисленных в порядке обхода границы многоугольника.
Составить алгоритм, определяющий, принадлежит ли точка (х0,y0)
многоугольнику.
2. Опишите, как по Вашему мнению должна работать программа,
помогающая завучу составлять расписание занятий в школе. Какие и в
каком виде должны быть представлены входные данные и результаты этой
программы?
780 3. а) Поэт-авангардист, сочиняющий "математические стихи"
последовательности чисел, хочет использовать компьютер для подбора
рифм. Для этого он создал словарь-массив всех допустимых натуральных
чисел, упорядоченных произвольно. Рифма - это пара различных чисел,
десятичные представления которых имеют на конце совпадающие
последовательности цифр; чем длиннее эти последовательности, тем
удачнее рифма.
Составить алгоритм, определяющий для заданного числа все наиболее
удачные рифмы, соответствующие этому числу. б) Как бы Вы посоветовали
поэту организовать словарь и алгоритм поиска рифм для слов русского
языкa? (Достаточно описать принцип работы алгоритма без его записи на
алгоритмическом языке).
781 4. а) Поэт Цветик хочет использовать компьютер для подбора рифм.
Для этого он создал словарь-массив литерных переменных, который
содержит все слова русского языка, со всеми их склонениями и
спряжениями; принцып упорядочения слов в словаре неизвестен. По
мнению Цветика, рифма - это пара различных слов, имеющих на конце
совпадающие подстроки ненулевой длины и чем длиннее эти подстроки,
тем удачнее рифма. Составить алгоритм, определяющий для заданного
слова все наиболее удачные рифмы.
б) Как известно, Незнайка нашел пару слов, оканчивающихся
одинаково, но не образующих рифму. Как бы Вы посоветовали Цветику
организовать словарь и алгоритм поиска рифм, чтобы не оказаться в
положении Незнайки? Инструкция: участник олимпиады должен решить три
задачи: первую, вторую и третью или четвертую на выбор. В задаче на
выбор задание б) является необязательным.
ПРАКТИЧЕСКИЙ ТУР
782 1. Написать программу, составляющую схему электрической цепи с
сопротивлением R из одинаковых резисторов с сопротивлением R0 (R и R0
натуральныe числа). В схеме должно быть как можно меньше резисторов.
Для справки:
- сопротивление цепи из последовательно соединенных резисторов R1,
R2,..., Rk равно R1 + R2 +... + Rk;
- сопротивление цепи из паралельно соединенных резисторов R1,
R2,..., Rk равно 1/(1/R1 + 1/R2 +... + 1/Rk);
- сумма сил токов, направленных в некоторый контакт, равна сумме
сил токов, направленных из этого контакта;
- для любого контура цепи, состоящего из k участков, верно: I1R1 +
I2R2 +... + IkRk = e1 + e2 +... + ek, где Ip - ток на p-м участке, еp
- э.д.с. на этом участке, Rp - сопротивление этого участка.
783 Т1. Пусть массив A состоит из N различных элементов. Составить
алгоритм, который находит K-й элемент по порядку убывания.
784 Т2. Выпуклый многоугольник задается координатами (X1,Y1),
(X2,Y2),..., (XN,YN) его N вершин. Координаты вершин являются
элементами соответствующих массивов X и Y. Триангуляцией выпуклого
N-угольника называется произвольное его разбиение на N-2 треугольника
с помощью N-3 непересекающихся диагоналей. Стоимостью триангуляции
называется сумма длин N-3 проведенных диагоналей. Составить алгоритм
поиска триангуляции наименьшей стоимости заданного многоугольника.
Для упрощения длиною диагонали, соединяющей вершины (XI,YI) и
(XJ,YJ), можно считать число |XI-XJ| +|YI-YJ|.
Практический тур.
785 П1. Русский текст зашифрован с помощью некоторого ключевого слова
таким образом:
1) Буквы ключевого слова пишутся много раз над буквами исходного
текста;
2) К алфавитному порядковому номеру каждой буквы текста
прибавляется алфавитный порядковый номер соответствующей буквы
ключевого слова;
3) Если результат превышает 32, из него вычитается 32;
4) Полученное число задает порядковый алфавитный номер буквы в
зашифрованном тексте. Например, исходные данные: КЛЮЧК ЛЮЧ КЛЮЧКЛЮЧКЛ
"ФРАЗА ДЛЯ ШИФРОВАНИЯ" (КЛЮЧ - ключевое слово) дадут следующий
результат: "ЯЬЯЯЛ РКЧ ГФУИЩОЯЕУЛ".
Буквы е и ? совпадают, все буквы строчные, латинские заменены
русскими с тем же написанием, знаки препинания не преобразуются,
длина ключевого слова равна 4. Зашифрованный текст содержит условие
второй задачи.
1. Расшифровать текст, если ключевое слово неизвестно. При
расшифровке рекомендуется использовать компьютер. Решение должно
содержать метод расшифровки с описанием использования ЭВМ, ключевое
слово и расшифрованный текст.
2. По желанию участник может попросить ключевое слово и
расшифровать текст. При это максимальное количество баллов за
практический тур уменьшается таким образом: если ключевое слово было
получено в течение 1-го часа, участник получает до 10% баллов, в
течение 2-го часа - 20%, в течение 3-го - 30%, 4-го - 40%.
3. Используя компьютер, решить вторую задачу.
Задача П2 была предложена в 4-х вариантах:
П2. Вариант 4: ШХСЯВъЛ УРКЧЙЖД М, ТЮНССЦЙЕБП У ГЙБОЧ, Й Т,
ъъЕХЩТБЙЙЛ Н ЗСЭЖЫ. ЦМРШъМУМ ШЬПУЩМНЬЬ, ЦПВЧЬБП ЛОПФСЮ ОРАМММЦЗЖ
ЧЦМШХЦФА ВЙНМШЯ М Й Т С УБЯСЭЬТЙСУ Т ЫМВЫСВФ Б ЛЭЖ ВЙЦЙХ АФТЫЙ,
ЦПВЧЬЬХ ъъЕХЩТБВъЛ Г Р С ЩЖ БЧРЖАПМУБИ О Г. ЭСЦБъСС ИЭЙГЖЭСЛ
ЮЫОШЖЭЫъГ Б ЦС ЕЮФТОЛ ъъГЯЙРБВЕ РСГМ Э ЕАЬППЬ.
786 Бизнес-турист.
Есть N стран и K видов товара. Бизнес-турист, гражданин 1-й
страны, имеет начальный капитал в M денежных единиц и намерен
получить на торговых операциях как можно больший капитал. Турист
может купить в родной стране любых товаров по своим финансовым
возможностям, поехать только в одну из других стран, продать там все
товары, в пределах имеющихся средств купить любых товаров, вернуться
домой и продать их.
Для каждой страны и каждого вида товара известна стоимость единицы
данного товара в данной стране (считается, что стоимости купли и
продажи равны).
Проезд должен быть оплачен. Для каждой зарубежной страны известна
стоимость проезда из первой страны в нее или обратно. Расчет за
поездку производится непосредственно перед ней. Все денежные суммы
представлены в одних единицах.
Напишите программу, которая:
вводит исходные данные из файла и выводит их на экран в виде
таблиц
позволяет человеку в диалоговом режиме задать маршрут поездки и
приобретаемые товары и рассчитывает расходы, доходы и текущее
состояние финансов
в ходе диалога проверяет правильность действий человека
определяет как можно более выгодные поездку и торговые операции
определяет, возможно ли вообще и выгодно ли при
заданных условиях заниматься бизнес-туризмом.
Технические условия
Поместите вашу программу-решение в текстовый ASCII-файл по имени
"C:\OLIMP\DAY-1\TOUR1-1.xxx".
Раcширение .xxx должно быть: .BAS для программ на Basic, .C для
программ на C, .PAS для программ на Pascal.
Программа должна прочитать входные данные из текстового ASCII-файла
"C:\OLIMP\DAY-1\TEST1-1.TXT".
Этот файл имеет такую структуру:
в его первой строке содержится количество стран N,
во второй - количество товаров K, в третьей -
начальный капитал M;
в следующих N строках содержатся стоимости товаров.
Каждая строка соответствует одной стране и содержит K чисел; каждые 2
соседних числа разделены пробелом. Эти числа равны стоимостям
соответствующих товаров в этой стране.
в следующей строке содержатся стоимости проезда. Строка содержит N-1
чисел; каждые 2 соседних числа разделены пробелом. Эти числа равны
стоимостям проезда в соответствующие страны. Стоимость проезда между
двумя странами не зависит от направления поездки.
Количества стран и видов товара не превосходят 20;
денежные суммы - целые числа, не превосходящие 32000 единиц.
Диалог и выходные данные оформляйте по образцу, приведенному ниже.
Пример
Входные данные:
3 {количество стран}
4 {количество видов товара}
10 {начальный капитал}
1 5 9 20 {стоимости товаров в 1-й стране}
5 9 1 80 {стоимости товаров во 2-й стране}
9 1 5 90 {стоимости товаров в 3-й стране}
1 2 {стоимости проезда из 1-й страны}
Эти данные подготовлены в файле
"C:\OLIMP\DAY-1\EX1-1.TXT". Вы можете использовать его для отладки.
Но успешная работа Вашей программы на этом примере не гарантирует
правильности вашей программы!
Оформление диалога и результатов
<запуск программы>
страны - 3, видов товара - 4, начальный капитал - 10
стоимости товара:
товарстрана1234115920259180391590
стоимости проезда:
куда13стоимость12
Выберите режим работы:
1 - диалог
2 - оптимизация
3 - выход
<человек выбирает 1>
<ответы человека следуют за вопросительными знаками>
Покупка товара(0-4)? 4 {0 - конец закупки товаров}
Сколько? 1
Не хватает денег
Покупка товара(0-4)? 2
Сколько? 1
Расход: 5, капитал: 5
Покупка товара(0-4)? 1
Сколько? 4
Расход: 4, капитал: 1
Покупка товара(0-4)? 0
Направление поездки(1-3)? 2
Расход: 1, капитал: 0
Товар продается в стране 2
Доход: 29, капитал: 29
Покупка товара(0-4)? 3
Сколько? 28
Расход: 28, капитал: 1
Покупка товара(0-4)? 0
Возврат в страну 1
Расход: 1, капитал: 0
Товар продается в стране 1
Доход: 252, капитал: 252
Будете анализировать другой маршрут(д/н)? д
Покупка товара(0-4)? 1
. . . . . .
Доход: 350, капитал: 350
Будете анализировать другой маршрут(д/н)? н
Выберите режим работы:
1 - диалог
2 - оптимизация
3 - выход
<человек выбирает 2>
<выполняется оптимизация>
Предлагаю маршрут:
Купить товар 1, количество единиц - 9
Поехать в страну 2
Продать товар
Купить товар 3,количество единиц - 44
Вернуться в страну 1
Продать товар
Итоговый капитал: 396
Выберите режим работы:
1 - диалог
2 - оптимизация
3 - выход
<человек выбирает 3>
<конец работы>
Cистема оценки:
до 3 баллов
до 10 баллов
до 10 баллов
до 70 баллов пропорционально полученной прибыли
до 7 баллов
787 Взаимозачет долгов (20 баллов).
Из-за экономического кризиса многие предприятия не могут получить
долги от покупателей и рассчитаться с продавцами за свои долги. Банк
намерен уменьшить общий долг своих клиентов, выполнив взаимозачет
долгов. Для этого банк может изменять долги клиентов любым образом
при условии, что для каждого клиента останется неизменным сальдо -
разница между суммой долгов ему и суммой его долгов. ЗАДАНИЕ:
Написать программу, которая преобразует заданный список долгов в
имеющий как можно меньшую общую сумму долгов.
Технические условия
Ваша программа должна прочитать входные данные для нескольких
тестов из одного текстового ASCII-файла DEBTS.DAT. Данные для
различных тестов отделены пустой строкой. Каждая строка файла
соответствует одному долговому обязательству и содержит 3 натуральных
числа: номер должника, номер предприятия, которому он должен, и сумму
долга. Соседние числа отделены пробелом.
Ваша программа должна записать результаты для всех тестов в один
текстовый ASCII-файл DEBTS.SOL, отделяя результаты различных тестов
пустой строкой. Результат каждого теста имеет содержать список
долгов, оставшихся после взаимозачетов. Этот список должен иметь
такую же структуру, что и входной. За ним надо вывести список сальдо
всех клиентов, которые были должниками или имели должников. Каждая
строка этого списка содержит номер предприятия и его сальдо,
отделенные пробелом. В конце результатов теста надо в отдельной
строке вывести общую сумму долгов.
Количество предприятий не превышает 100, денежные суммы не
превышают 30000 единиц.
Имя файла с исходным текстом программы - DEBTS.*.
Пример
Входные данные (файл DEBTS.DAT):
1 2 100
2 3 50
3 1 75
1 2 15
2 3 11
4 1 14
Выходные данные (файл DEBTS.SOL) должны выглядеть так:
1 2 25
3 2 25
1 -25
2 50
3 -25
50
1 2 1
4 2 4
4 3 11
1 -1
2 4
3 11
4 -14
15
788 Сравнение компостеров
(20 баллов)
Компостер в автобусе делает в билете отверстия, что содержатся в
некоторых узлах квадратной сетки размером M*N узлов. Компостеры
считаются одинаковыми, если все сделанные ими отверстия в билетах
можно совместить, отобразив один билет на другой комбинацией
параллельных переносов, поворотов на прямой угол и симметрий
относительно горизонтальной и вертикальной осей. Закомпостированный
билет имеет по крайней мере одно отверстие.
ЗАДАНИЕ: Написать программу, определяющую, одинаковы ли два
заданных компостера.
Технические условия
Ваша программа должна прочитать входные данные для нескольких
тестов из одного текстового ASCII-файла COMPOST2.DAT. Данные для
различных компостеров отделены пустым строкой. Каждый строка файла
соответствует одному строке компостера и содержит единицы (отверстия)
и нули (узлы без отверстий). Соседние числа отделены пробелом.
Ваша программа должна записать результаты для всех тестов в один
текстовый ASCII-файл COMPOST2.SOL. Результат каждого теста - строка
из его порядковым номером и словом "Одинаковые" или "Разные".
Размеры сетки не превышают 15*15 узлов.
Имя файла с исходным текстом программы - COMPOST2.*.
Пример
Входные данные (файл COMPOST2.DAT):
0 0 0 {первый тест, первый компостер}
0 0 1
0 0 0
0 1 0 0 {первый тест, второй компостер}
0 0 0 0 {хоть он и имеет не такой размер, как первый}
0 0 0 0 {но считается одинаковым с ним}
1 0 0 0 0 0 {второй тест, первый компостер}
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 1 0
1 0 0 0 0 1 {второй тест, второй компостер}
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
Выходные данные (файл COMPOST2.SOL) должны выглядеть так:
1 Одинаковые
2 Разные
789 Количество компостеров
(60 баллов)
ЗАДАНИЕ: Написать программу, которая при условии предыдущей за-
дачи определит количество различных компостеров, которые можно
образовать на сетке размером M*N узлов.
Технические условия
Ваша программа должна прочитать входные данные для нескольких
тестов из одного текстового ASCII-файла COMPOST3.DAT. Каждая строка
файла соответствует одному тесту и содержит числа M и N, разделенные
пробелом
Ваша программа должна записать результаты для всех тестов в один
текстовый ASCII-файл COMPOST3.SOL. Результат каждого теста - строка с
его порядковым номером и количеством компостеров.
M и N не превосходят 15.
Имя файла с исходным текстом программы - COMPOST3.*.
Пример
Входные данные (файл COMPOST3.DAT):
1 1
2 2
Выходные данные (файл COMPOST3.SOL) должны выглядеть так:
1 1
2 5
Второй тур
27 марта 1994 г
790 Архиватор
Напишите программу-архиватор, преобразующую входной текстовый файл
в выходной (архивный) файл как можно меньшего размера, и
программу-дезархиватор, восстанавливающую по архивному файлу исходный
(50 баллов).
Напишите программу-архиватор, преобразующую все текстовые файлы с
именами, соответствующими маске "*.txt", находящиеся в текущем
каталоге, в один выходной (архивный) файл как можно меньшего размера,
и программу-дезархиватор, восстанавливающую по архивному файлу все
входящие в него текстовые файлы (30 баллов).
По разным причинам информация в архивных файлах может искажаться.
Добавьте в дезархиватор средства, предупреждающие человека в случае
искажения информации в архивном файле (20 баллов).
Технические условия
Входные текстовые файлы могут содержать большие и малые
украинские, русские и латинские буквы, цифры, точки, запятые, точки с
запятой, двоеточия, вопросительные и восклицательные знаки, тире,
двойные кавычки, открывающие и закрывющие круглые скобки, пробелы,
символы возврата каретки (десятичный код - 10) и перевода строки (код
13). Каждый файл завершается символом конца файла (код 26). Длина
строк не превосходит 255 символов. Используйте кодировку украинских
букв, соответствующую предоставленному Вам драйверу.
Архiвний файл повинен завершуватися символом кiнця файлу; в
серединi архiвного файлу цей символ мiститися не може.
Архивный файл должен заканчиваться символом конца файла; в
середине архивного файла этот символ находиться не может.
Программы должны запрашивать необходимые имена текстовых и
архивных файлов в диалоге.
Откомпилированные программы должны обрабатывать каждый набор
тестовых текстов не дольше, чем за 5 минут; интерпретируемые - не
дольше, чем за 10 минут. Имена файлов с исходными текстами программ -
ARC.* и UNARC.*
791 Стеклянный забор
Имя входного файла: |
swamp.in |
Имя выходного файла: |
swamp.out |
Ограничение по времени: |
2 секунды |
Ограничение по памяти: |
64 мегабайта |
Максимальная оценка |
100 баллов |
В известном городе Санкт-Тверь решили построить новый микрорайон, представляющий в плане прямоугольную область. Границы микрорайона и его улицы по проекту ориентированы строго по сторонам света, причем улицы разбивают микрорайон на кварталы размером 1 км × 1 км.
В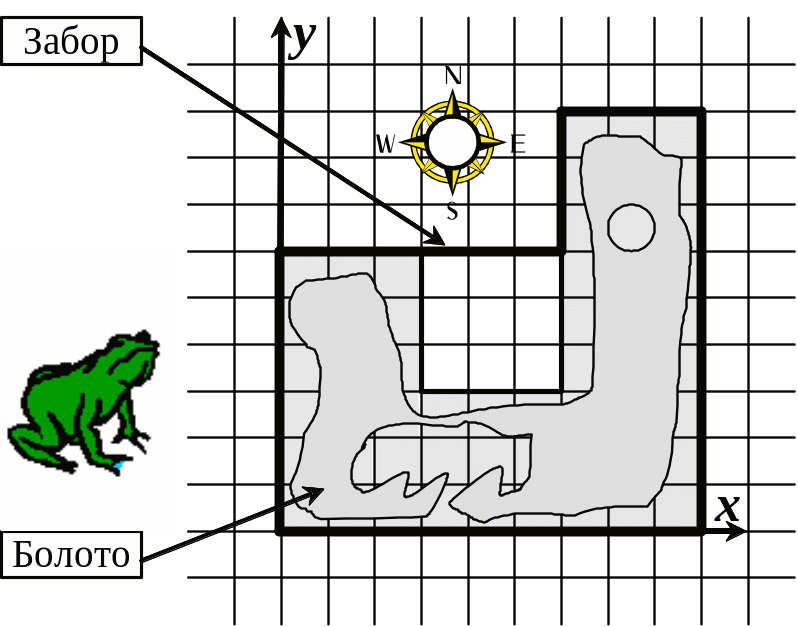 о
время привязки исходного проекта к
местности выяснилось, что некоторые
кварталы по проекту микрорайона
оказываются полностью или частично
расположенными на топком болоте. Область,
занимаемая болотом, связна и со всех
сторон окружена подлежащими застройке
кварталами микрорайона (область связна,
если из любой ее точки можно добраться
в любую другую, не выходя за пределы
области).
о
время привязки исходного проекта к
местности выяснилось, что некоторые
кварталы по проекту микрорайона
оказываются полностью или частично
расположенными на топком болоте. Область,
занимаемая болотом, связна и со всех
сторон окружена подлежащими застройке
кварталами микрорайона (область связна,
если из любой ее точки можно добраться
в любую другую, не выходя за пределы
области).
Для сохранения экологии местности и обеспечения безопасности жителей занятую болотом область решили оградить стеклянным забором. Забор должен проходить только по границам кварталов проектируемого микрорайона, отделяя болото, и, возможно, некоторые кварталы проекта, не занятые болотом, от остальной части микрорайона.
Для экономии строительных материалов забор должен иметь минимальную длину. Среди всех заборов минимальной длины нужно выбрать тот, для которого площадь части микрорайона, попадающей внутрь забора, минимальна.
Требуется написать программу, которая спроектирует забор с заданными выше свойствами.
Формат входных данных
Входной файл содержит описание многоугольника — границы области, состоящей только из кварталов c заболоченными участками. Стороны многоугольника параллельны осям координат.
В первой строке задано целое число n — количество вершин в многоугольнике (4 ≤ n ≤ 100 000, n четное). В каждой из следующих n строк заданы два целых числа — координаты очередной вершины при обходе этого многоугольника против часовой стрелки. Все числа не превосходят 109 по абсолютной величине. Никакие три последовательные вершины границы не лежат на одной прямой. Граница многоугольника не содержит самопересечений и самокасаний.
Формат выходных данных
Выходной файл должен содержать описание многоугольника, определяющего искомый забор. Формат описания многоугольника тот же, что и для входных данных. Никакие три последовательные вершины этого многоугольника не должны лежать на одной прямой.
Пример
swamp.in |
swamp.out |
8 0 0 9 0 9 9 6 9 6 3 3 3 3 6 0 6 |
6 0 0 9 0 9 9 6 9 6 6 0 6 |
792 Школа танцев
Имя входного файла: |
dance.in |
Имя выходного файла: |
dance.out |
Ограничение по времени: |
2 секунды |
Ограничение по памяти: |
64 мегабайта |
Максимальная оценка |
100 баллов |
В школу бальных танцев профессора Падеграса записались n учеников — мальчиков и девочек. Профессор построил их в один ряд, и хочет отобрать из них для первого занятия группу стоящих подряд учеников, в которой количество мальчиков и девочек одинаково. Сколько вариантов выбора есть у профессора?
Формат входных данных
В первой строке входного файла задано число n (1 ≤ n ≤ 106). Во второй строке задается описание построенного ряда из мальчиков и девочек — строка из n символов a и b (символ a соответствует девочке, а символ b — мальчику).
Формат выходных данных
В единственной строке выходного файла должно содержаться единственное число — количество вариантов выбора требуемой группы.
Примеры
dance.in |
dance.out |
3 bab |
2 |
8 abbababa |
13 |
Несчастливые номера
Имя входного файла: |
unlucky.in |
Максимальная оценка |
100 баллов |
Обычно автобусный билет с номером, состоящим из 6 цифр, считается счастливым, если сумма первых трех цифр его номера была равна сумме трех последних. Школьник Вася очень любил получать счастливые билеты, однако это случалось не так часто. Поэтому для себя он изменил определение счастливого билета.
Счастливым он считал тот номер, сумма некоторых цифр которого равнялась сумме оставшихся цифр. В его представлении билет с номером 561743 счастливый, так как 5+1+4+3=6+7.
Вася вырос, но по привычке в номерах различных документов пытается найти признаки счастливого номера . Для этого он расширил свое определение счастливого номера на n‑значные номера лицевых счетов и других документов, состоящих из цифр от 0 до k (1 ≤ k ≤ 9). Номер документа он называет счастливым, если сумма некоторых цифр этого номера равняется сумме оставшихся. Остальные номера для него несчастливые. К сожалению, несмотря на расширенное понимание “счастья”, несчастливых номеров остается еще много...
Вам предлагается определить количество несчастливых n-значных номеров, которые можно составить, используя цифры от 0 до k. В номерах допускается любое количество ведущих нулей.
Входной файл unlucky.in находится в каталоге c:\work\unlucky вашего компьютера. Файл содержит описание нескольких видов номеров. Каждый вид номеров определяется значениями n и k. Для данного входного файла вы должны создать соответствующий ему выходной файл и отправить его на проверку жюри.
Формат входных данных
Входной файл содержит несколько пар значений n и k, каждая пара записана в отдельной строке.
Формат выходных данных
Для каждой пары значений n и k входного файла выведите в соответствующей строке выходного файла искомое количество несчастливых билетов или 0, если такое число вам получить не удалось. Количество строк во входном и выходном файлах должно совпадать.
Примечания
За правильное решение задачи для каждого вида номеров вы получите 5 баллов. Так, представленный в примере выходной файл соответствует 15 баллам.
При сдаче на проверку выходного файла во время тура вы будете получать одно из двух сообщений:
Presentation Error — если файл не соответствует формату вывода. В этом случае файл не принимается на проверку.
Accepted — если файл формату вывода соответствует. В этом случае файл принимается на проверку. Проверка правильности ответов в выходном файле осуществляется только после окончания тура.
793 Счастливые цифры
Имя входного файла: |
lucky.in |
Имя выходного файла: |
lucky.out |
Ограничение по времени: |
2 секунды |
Ограничение по памяти: |
64 мегабайта |
Максимальная оценка |
100 баллов |
Школьнику Васе нравятся числа, которые заканчиваются счастливыми для него цифрами k. Поэтому каждый раз, когда он видит какое-нибудь натуральное число n, он сразу пытается подобрать такое d (d ≥ 2), что число n в системе счисления с основанием d заканчивается как можно большим количеством цифр k.
Требуется написать программу, которая по заданным числам n и k найдет такое d, чтобы число n в системе счисления с основанием d заканчивалось как можно большим количеством цифр k.
Формат входных данных
Входной файл содержит два целых десятичных числа n и k (1 ≤ n ≤ 1011; 0 ≤ k ≤ 9).
Формат выходных данных
В выходной файл выведите два числа: d — искомое основание системы счисления и l —количество цифр k, которым заканчивается запись числа n в этой системе счисления. Если искомых d несколько, выведите любое из них, не превосходящее 1012 (такое всегда существует).
Примеры
lucky.in |
lucky.out |
комментарий |
49 1 |
3 2 |
4910 = 12113 |
7 5 |
3 0 |
Ни в одной системе счисления 7 не заканчивается на цифру 5 |
794 Тапкодер
Имя входного файла: |
topcoder.in |
Имя выходного файла: |
topcoder.out |
Ограничение по времени: |
2 секунды |
Ограничение по памяти: |
64 мегабайта |
Максимальная оценка |
100 баллов |
Ассоциация Тапкодер организует Всемирное парное соревнование сильнейших программистов. К участию в соревновании допущены первые 2k зарегистрировавшихся участников, которым присвоены номера от 1 до 2k.
Соревнование будет проходить по олимпийской системе. В первом туре первый участник встречается со вторым, третий с четвертым и так далее. В каждой паре победителем становится участник, первым решивший предложенную задачу, при этом ничьих не бывает. Все победители очередного тура и только они являются участниками следующего тура. В каждом туре пары составляются из участников в порядке возрастания присвоенных им номеров. Соревнование продолжается до тех пор, пока не останется один победитель.
Организаторам стало известно, что некоторые пары участников заранее договорились о результате встречи между собой, если такая встреча состоится. Для всех остальных встреч, кроме n договорных, возможен любой исход.
Некоторые m участников соревнования представили свои резюме в ассоциацию Тапкодер с целью поступления на работу. Организаторов интересует, до какого тура может дойти каждый из претендентов при наиболее благоприятном для него стечении обстоятельств. При этом для каждого участника в отдельности считается, что все недоговорные встречи, в том числе те, в которых он не участвует, закончатся так, как ему выгодно, а все состоявшиеся договорные встречи закончатся в соответствии с имеющимися договоренностями.
Требуется написать программу, которая для каждого из претендентов определяет максимальный номер тура, в котором он может участвовать.
Формат входных данных
В первой строке входного файла заданы три целых числа k (1 ≤ k ≤ 60), n (0 ≤ n ≤ 100 000) и m (1 ≤ m ≤ 100 000). В следующих n строках описаны n пар участников, которые договорились между собой о том, что первый из двух участников пары выиграет встречу, если она состоится. Гарантируется, что каждая пара участников присутствует во входных данных не более одного раза, при этом, если задана пара x y, то пары y x быть не может, кроме того, x ≠ y. В последней строке файла перечислены номера участников, желающих работать в Тапкодере, в порядке возрастания их номеров. Все номера претендентов на работу различны.
Формат выходных данных
Выходной файл должен содержать m целых чисел — максимальные номера туров, до которых могут дойти соответствующие претенденты на работу. Туры нумеруются от 1 до k.
Примеры
topcoder.in |
topcoder.out |
комментарий |
2 0 3 1 3 4 |
2 2 2 |
У каждого из участников есть возможность выйти в финал, так как договорных матчей нет |
3 1 1 3 1 1 |
3 |
Если четвертый участник выиграет у третьего, то договорная встреча первого и третьего не состоится, что благоприятно для первого |
3 3 4 1 2 1 3 4 1 1 2 3 4 |
3 1 2 3 |
Первому участнику благоприятно во втором туре играть с третьим, а не с четвертым, в свою очередь, четвертый может выиграть у третьего и также выйти в финал |
795 Две строки
Имя входного файла: |
twostr.in |
Имя выходного файла: |
twostr.out |
Максимальное время работы на одном тесте: |
2 секунды |
Максимальный объем используемой памяти: |
64 мегабайта |
Максимальная оценка |
100 баллов |
Циклическим сдвигом строки s0s1…sn-1 на k позиций назовем строку sksk+1…sns1..sk-1. Например, циклическим сдвигом строки «abcde» на две позиции является строка «cdeab». В этой задаче далее будут рассматриваться только строки, состоящие из десятичных цифр от 0 до 9. Произвольной такой строке, первый символ которой не является нулем, можно сопоставить число, десятичной записью которого она является. Строкам, которые начинаются с нуля, никакое число сопоставляться не будет. Например, строке 123 сопоставляется число сто двадцать три, а строке 0123 не сопоставляется никакое число.
Пусть заданы две строки: s и t. Обозначим как S набор всех циклических сдвигов строки s, а как T – набор всех циклических сдвигов строки t. Например, если s = «1234», то S содержит строки «1234», «2341», «3412», «4123». Обозначим также как NUM(A) набор чисел, соответствующих строкам из набора A.
Требуется написать программу, которая по строкам s и t определит, максимальное число, представимое в виде разности (x – y), где x принадлежит NUM(S), а y принадлежит NUM(T). Например, если s = «25», t = «12», то NUM(S) содержит числа 25 и 52, NUM(T) – числа 12 и 21; их попарными разностями будут: 25 – 12 = 13, 25 – 21 = 4, 52 – 12 = 40, 52 – 21 = 31. Из этих разностей максимальным числом является 40.
Формат входных данных
Первая строка входного файла содержит строку s, вторая строка входного файла – строку t. Обе строки непустые. Они содержат только цифры, из которых хотя бы одна не является нулем. Строки имеют длину не более 3000 символов.
Формат выходных данных
В выходной файл выведите искомое число без ведущих нулей.
Примеры входных и выходных данных
twostr.in |
twostr.out |
25 12 |
40 |
100 1 |
99 |
Замечания о системе оценки
1) Решения, которые выдают правильные ответы только для строк s и t, длина которых не превосходит 9 символов, будут оцениваться из 40 баллов.
2) Решения, которые выдают правильные ответы только для строк s и t, длина которых не превосходит 200 символов, будут оцениваться из 60 баллов.
796 Скользящая симметрия
Имя входного файла: |
motion.in |
Имя выходного файла: |
motion.out |
Максимальное время работы на одном тесте: |
2 секунды |
Максимальный объем используемой памяти: |
64 мегабайта |
Максимальная оценка |
100 баллов |
Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если A1 и B1 – образы некоторых точек A и B при движении, то |A1B1| = |AB|.
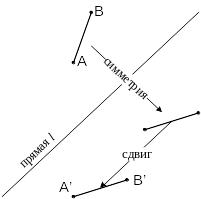
Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой l и переноса на вектор, параллельный l (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.
|
Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии.
Требуется по координатам двух различных точек A и B и двух точек A1 и B1, находящихся на таком же расстоянии друг от друга, как и точки A и B, найти скользящую симметрию, переводящую точку A в точку A1, а точку B в точку B1.
Формат входных данных
В первой строке входного файла находятся четыре целых числа – координаты двух различных точек A и В. Во второй строке также находятся четыре целых числа – координаты двух различных точек A1 и В1. Гарантируется, что |A1B1| = |AB|. Все числа во входном файле по модулю не превышают 1000. Числа в строках разделены пробелом.
Формат выходных данных
Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.
В первой строке должны выводиться координаты двух различных точек, лежащих на прямой l, относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.
Пример входных и выходных данных
motion.in |
motion.out |
1 1 3 2 -1 1 -3 2 |
0.000000 0.000000 0.000000 1.000000 0.000000 0.000000 |
1 1 3 1 3 -1 5 -1 |
0.000000 0.000000 1.000000 0.000000 2.000000 0.000000 |
797 Трехмерный тетрис
Имя входного файла: |
tetris.in |
Имя выходного файла: |
tetris.out |
Максимальное время работы на одном тесте: |
2 секунды |
Максимальный объем используемой памяти: |
64 мегабайта |
Максимальная оценка |
100 баллов |
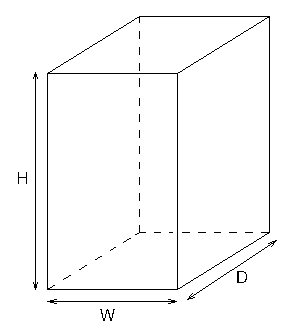
Игра в трехмерный тетрис происходит на поле, имеющем вид прямоугольного параллелепипеда размером W D H единичных кубиков. Введем координатную систему так, чтобы один из углов параллелепипеда находится в точке (0, 0, 0), противоположный ему – в точке (W, D, H), а ребра параллелепипеда были параллельны осям координаты. Каждый единичный кубик поля можно задать максимальными координатами его углов, тогда кубики будут иметь координаты от (1, 1, 1) до (W, D, H).
В процессе игры на поле последовательно появляются фигуры. Каждая фигура представляет собой множество единичных кубиков и обладает следующим свойством: от любого кубика можно добраться до любого другого, переходя через общую грань.
Игрок может сделать несколько действий с фигурой. Каждое действие является либо перемещением ее на один в направлении одной из осей координат, либо поворотом ее на 90 градусов вокруг одной из координатных осей. Один из кубиков в фигуре является базовым – при поворотах он остается на месте. При повороте фигура сначала исчезает с игрового поля, и затем появляется снова, уже в новом положении. Направления поворотов показаны на рисунке, при повороте вокруг оси OX ось OY переходит в ось OZ, при повороте вокруг оси OY ось OZ переходит в ось OX, при повороте вокруг оси OZ ось OX переходит в ось OY. Базовый кубик при повороте остается на месте.
|
|
Требуется написать программу модуля, ответственного за определение кубиков, которые в результате игры окажутся заняты фигурами. Заранее известна последовательность появления фигур на поле и действия с этими фигурами, которые произвел игрок. Гарантируется, что каждое из действий допустимо, то есть не происходит выхода фигуры за границу поля, и не происходит появления у двух фигур общего кубика.
Формат входных данных
В первой строке входного файла содержатся размеры игрового поля – три целых числа W, D и H (1 ≤ W, H, D ≤ 100).
Во второй строке входного файла задано целое число n – количество фигур, которые были размещены на игровом поле. (0 ≤ n ≤ 100). Каждая фигура задается следующим образом: на первой строке задано натуральное число m - количество кубиков в фигуре. (1 ≤ m ≤ 100) Далее следуют m строка, в i-й из которых содержится тройка целых чисел xi, yi, zi – координаты i-го кубика в фигуре в ее начальном положении. Базовый кубик описывается первым.
Следующая строка содержит целое число k – количество операций, которые были проведены игроком с данной фигурой (0 ≤ k ≤ 100). Далее следуют k строк. Каждая из них начинается либо со слова «shift», либо со слова «rotate».
В первом случае далее следует одна из букв «x», «y» или «z», обозначающая, вдоль какой из осей был выполнен сдвиг, после чего через пробел идет либо символ «+», если сдвиг был осуществлен в положительном направлении данной оси, либо «–», если сдвиг был осуществлен в отрицательном направлении.
Если же строка начинается со слова «rotate», то далее идет одна из букв «x», «y» или «z», обозначающая, вокруг какой из осей был выполнен поворот.
Формат выходных данных
Выведите в выходной файл в произвольном порядке координаты всех кубиков, которые будут заняты фигурами. На каждой строке должно содержаться три числа, разделенных пробелом – координаты кубика в формате «x y z».
Примеры входных и выходных данных
tetris.in |
tetris.out |
2 2 2 1 2 1 1 1 2 1 1 1 shift z + |
2 1 2 1 1 2 |
3 3 3 1 4 2 2 2 3 2 2 2 3 2 2 2 3 2 rotate y rotate z |
2 2 2 2 3 2 2 2 1 1 2 2 |
Замечание о системе оценки
Решения, обрабатывающие только сдвиги фигур, будут оцениваться из 40 баллов.
798
 Задача
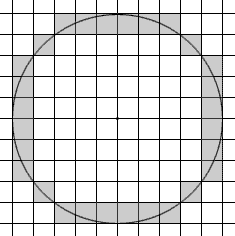
1. Окружность (15
баллов)
Задача
1. Окружность (15
баллов)
На листочке в клеточку нарисована окружность радиуса R клеток с центром на пересечении двух линий. Необходимо найти количество клеток, по которым проходит окружность. (Если окружность только касается границы клетки, клетку считать не надо).
Входные данные
Во входном файле INPUT.TXT содержится единственное число R (R 30000).
Выходные данные
Выходной файл OUTPUT.TXT должен содержать одно число – искомое количество клеток.
Пример INPUT.TXT: OUTPUT.TXT для примера:
5 28
Ограничение времени: 1 сек на тест
799 Задача 2. Гири (23 балла)
По случаю юбилея Палаты Мер и Весов (N лет со дня основания) решено выпустить сувенирный набор гирь. Вес любой гири должен выражаться целым числом, в наборе не должно быть гирь одинакового веса, суммарный вес гирь должен равняться N. Кроме того, требуется, чтобы из набора можно было бы составить любой целый вес от 1 до N взяв часть гирь. При этом количество гирь в наборе должно быть минимально возможным. Необходимо найти набор гирь, удовлетворяющий этим условиям (любой в случае нескольких вариантов).
Входные данные
Во входном файле INPUT.TXT содержится единственное число N (N 1000000).
Выходные данные
В первой строке выходного файла OUTPUT.TXT должно содержаться количество гирь. Во второй строке – веса гирь через пробел. Если набора не существует, вывести 0.
Пример INPUT.TXT: один из вариантов OUTPUT.TXT для примера:
17 5 1 2 3 5 6
Пример INPUT.TXT: OUTPUT.TXT для примера:
4 0
Ограничение времени: 1 сек на тест
800 Задача 3. Посты ГИБДД (27 баллов)
На автомобильной трассе Москва-Иркутск проходит реорганизация постов ГИБДД. Для оптимального решения задачи расстановки постов выявлено N (N 8000) маршрутов (участков) наиболее активного движения. Участки могут пересекаться, каждый участок задаётся парой чисел [ai, bi] – номером начального и конечного пункта (все пункты трассы пронумерованы от 1 до L, L 50000). Для каждого участка определена его степень важности – число ci. Требуется так выбрать пункты установки постов, чтобы на каждом участке наиболее активного движения количество установленных постов было бы не меньше его степени важности. (Пост, установленный на границе участка считается принадлежащим участку. В одном пункте нельзя установить сразу два поста.) Кроме того, необходимо, чтобы количество постов было минимально возможным.
Входные данные
Первая строка входного файла INPUT.TXT содержит целое число N (1 N 8000) – количество участков. Следующие N строк описывают участки. Строка i+1 входного файла содержит три целых числа ai, bi, ci (границы отрезка и его степень важности), разделенные одиночными пробелами и такие, что 1 ai bi 50000 и 1 ci bi-ai+1.
Выходные данные
В первой строке выходного файла OUTPUT.TXT должно содержаться целое число K – количество устанавливаемых постов. Во второй строке – K чисел – номера пунктов, в которых устанавливаются посты. Все номера пунктов должны быть различны.
Пример INPUT.TXT: один из вариантов OUTPUT.TXT для примера:
5 6 3 7 3 3 5 6 8 9 10 8 10 3 6 8 1 1 3 1 10 11 1
Ограничение времени: 5 сек на тест
801 Задача 4. Трёхцветная плитка (35 баллов)
Пол прямоугольной комнаты покрывают плиткой. Размер комнаты – M на N плиток. Каждый раз мастер берет верхнюю плитку из стопки и укладывает ее. После этого переходит к укладке одной из соседних плиток (т.е. имеющих общую сторону с уже уложенной). Плитки, которые укладывает мастер – трёх разных цветов и известно, что в стопке, из которой их брал мастер, они лежали в порядке чередования цветов. То есть 1, 2, 3, 1, 2, 3, … и т.д., считая сверху стопки (цвета обозначаются цифрами 1, 2 и 3). В результате работы мастер выложил плиткой весь пол комнаты. Известно, что начал мастер с первой плитки в первом ряду (верхний левый угол на рисунке) и, конечно же, дважды на одно и то же место плитку не клал. Вам по полученному рисунку требуется определить маршрут мастера (то есть в каком порядке он выбирал места для укладки плитки).
Входные данные
В первой строке входного файла INPUT.TXT содержатся числа M и N (M, N 100), разделённые пробелом. Далее в M строках содержится по N чисел (1, 2 или 3), задающих цвет соответствующей плитки, разделённых пробелом.
Выходные данные
Выходной файл OUTPUT.TXT должен содержать M·N строк. В каждой (i-ой) строке – по два числа: номер строки и номер позиции в строке места, на которое мастер укладывал плитку на i-ом шаге. Строки и позиции в строке нумеруются с 1. Если узор не мог быть построен при соблюдении условий задачи, вывести единственное число 0.
Пример INPUT.TXT: OUTPUT.TXT для примера:
3 3 1 1 1 2 3 1 2 3 2 1 1 3 1 2 3 2 3
2 2
2 1
3 1
3 2
3 3 Ограничение времени: 2 сек на тест
802 Задача 1. Остаток от деления на 5 (18 баллов) ограничение времени: 1 сек на тест
Дано число в шестнадцатеричной системе счисления. Необходимо найти остаток от деления этого числа на 5.
Входные данные
Во входном файле INPUT.TXT содержится последовательность цифр (используются цифры 0, 1, 2, …, 9, A, B, C, D, E, F), задающая число в шестнадцатеричной системе счисления. Количество цифр – не более 100.
Выходные данные
В выходной файл OUTPUT.TXT вывести одну цифру – остаток от деления на 5.
Пример INPUT.TXT: OUTPUT.TXT для примера:
FF 0
803 Задача 2. Функциональный язык. (35 баллов) ограничение времени: 1 сек на тест
В языке программирования ОГОЛ вызывать функции можно лишь из функций, которые описываются после описания той функции, которая вызывается. В частности, функция не может вызывать себя.
Программист Петя спроектировал программу, которая должна быть написана на этом языке. В проекте указано, какие функции вызываются из каждой функции. Для удобства Петя пронумеровал все функции числами от 1 до N.
Требуется написать программу, которая определяет, в каком порядке функции должны быть описаны в программе на языке ОГОЛ.
Входные данные
В первой строке входного файла INPUT.TXT содержится число N (1 N )- количество функций, которые должны быть в программе. Далее идут N строк, причем i-ая строка содержит описание функций, которые должны вызываться из i-ой функции. Это описание содержит сначала число Ai (0 Ai N) - количество функций, которые вызываются из данной функции, а затем номера вызываемых функций (одна и та же функция может вызываться из некоторой функции несколько раз).
Выходные данные
В выходной файл OUTPUT.TXT необходимо вывести номера функций в том порядке, в каком они должны быть описаны в программе. Если написать такую программу на языке ОГОЛ невозможно, в выходной файл нужно поместить одно число 0.
Пример INPUT.TXT: Пример INPUT.TXT:
3 2
0 1 2
3 1 1 3 1 1
1 1
OUTPUT.TXT для примера: OUTPUT.TXT для примера:
1 3 2 0
804 Задача 3. Хромая ладья (40 баллов) ограничение времени: 2 сек на тест
Гриша и Дима играют в следующую игру: они передвигают по клетчатому полю размером M на N “хромую ладью”. Гриша и Дима по очереди делают ходы. Каждым ходом один из игроков передвигает хромую ладью на некоторое количество клеток (от 1 до K) вправо, либо на некоторое количество клеток (от 1 до L) вверх. В начале игры хромая ладья стоит в левом нижнем углу доски. Выигрывает тот, кто поставит ладью в правый верхний угол.
Требуется написать программу, определяющую первый ход первого игрока, который обеспечивает ему выигрыш при дальнейшей правильной игре.
Входные данные
Входной файл INPUT. TXT состоит из одной строки. В ней записаны числа M, N, K и L (через пробел). 1 M, N, K, L 200. M – количество горизонталей доски, N – количество вертикалей, K – максимально возможное количество клеток при ходе вправо, L – максимально возможное количество клеток при ходе вверх. Числа в строке разделены пробелами.
Выходные данные
В выходной файл OUTPUT.TXT необходимо вывести два числа – смещение ладьи вправо и вверх. При ходе вправо на R клеток это будет R 0, при ходе вверх на R клеток – 0 R. Если хода, обеспечивающего победу, не существует, вывести два нуля.
Пример INPUT.TXT: Пример INPUT.TXT:
2 4 2 2 2 2 1 1
один из вариантов OUTPUT.TXT OUTPUT.TXT для примера:
для примера: 0 0
0 1
805 Задача 4. Кладотолкатель (57 баллов) ограничение времени: 1 сек на тест
Некий лабиринт представляет собой матрицу M x N, некоторые ячейки которой пустые, а остальные заполнены камнями. В одной из пустых ячеек находится клад, а в другой – кладоискатель. Кладоискатель может передвигаться в соседнюю ячейку (соседними считаются ячейки, граничащие по стороне), а также передвигать клад следующим образом: нужно встать в соседнюю к кладу ячейку и толкнуть его. Тогда клад передвинется на соседнюю ячейку в направлении, заданном толчком (от кладоискателя к кладу), а кладоискатель переместится в ячейку, где только что находился клад. При этом кладоискатель и клад не могут перемещаться в ячейку, заполненную камнем, за пределы лабиринта, а также кладоискатель не может становиться в ячейку, в которой находится клад, не толкая его.
Требуется написать программу, которая определяет последовательность толчков и передвижений кладоискателя, передвигающую клад к выходу. Так как клад очень тяжёлый, количество толчков должно быть минимальным.
При наличии нескольких решений программа должна выводить то из них, которое состоит из наименьшего количества перемещений.
Входные данные
Первая строка входного файла содержит числа М и N (1 M, N 30). Последующие М строк содержат описание лабиринта. Каждая строка состоит из N символов, описывающих ячейки лабиринта: заполненная камнями ячейка обозначается латинской буквой 'Х' пустая ячейка обозначается символом '.' (ASCII код 46), начальная позиция кладоискателя – буквой 'Y', начальная позиция клада – латинской буквой 'В', выход – латинской буквой 'T'.
Выходные данные
Если решения не существует, то файл OUTPUT.TXT должен содержать число 0. Иначе, в первой строке выходного файла должно содержаться количество перемещений K, а во второй строке - последовательность K символов, определяющая действия кладоискателя. Символы 'w', 'e', 'n', 's' обозначают передвижения кладоискателя на запад, восток, север и юг соответственно, а символы 'W', 'Е', 'N', 'S' обозначают толчки кладоискателя в соответствующих направлениях.
Пример INPUT.TXT: OUTPUT.TXT для примера:
3 3 5
..Y sWnwS
.B.
TXX
806 Задача 1. Вырежем шахматную доску (30 баллов) ограничение времени: 1 сек на тест
Из прямоугольника размером M на N, клетки которого раскрашены в черный и белый цвет, требуется вырезать квадрат размера K на K, раскрашенный в шахматном порядке (то есть любые две соседние клетки раскрашены в разные цвета).
Входные данные
В первой строке входного файла INPUT.TXT записаны числа M, N, K (1 K M, N 900) через пробел. В последующих M строках расположены N чисел 0 или 1, задающие цвета клеток прямоугольника.
Выходные данные
Программа должна выводить в первую и единственную строку выходного файла OUTPUT.TXT номера строки и столбца клетки – левого верхнего угла вырезаемой доски. Числа должны разделяться пробелом. Если требуемый квадрат вырезать невозможно, программа должна выводить одно число 0.
Пример INPUT.TXT: OUTPUT.TXT для примера:
3 4 2 2 3
1 1 1 0
1 1 1 0
1 1 0 1
807 Задача 2. Прибавлятель (30 баллов) ограничение времени: 1 сек на тест
Некоторое устройство, называемое «Прибавлятель», оперирует с числом, записанным на ленте. В каждый момент времени Прибавлятель работает только с одной из цифр числа на ленте (говорят, что он находится над этой цифрой), выполняя одну из двух команд: "<" –передвинуться на одну цифру (позицию на ленте) влево, и "+" - изменить цифру, над которой он находится в данный момент: 1 изменяется на 2, 2 – на 3, 3 – на 4, 4 – на 5; 5 – на 6, 6 – на 7, 7 – на 8, 8 – на 9, 9 – на 0, 0 – на 1. Если Прибавлятель выполняет команду "<", находясь над самой левой цифрой числа на ленте, то к этому числу слева приписывается цифра 0, и Прибавлятель оказывается над ней. В исходном состоянии Прибавлятель находится над крайней правой цифрой числа на ленте.
Требуется написать программу, формирующую такую последовательность команд Прибавлятеля, после выполнения которой к заданному числу А на ленте прибавится число В.
Входные данные
В первой строке входного файла содержится число, напечатанное на ленте (натуральное число, не более 250 цифр). Вторая строка содержит число (натуральное, не более 250 цифр), которое нужно прибавить к числу на ленте.
Выходные данные
В единственной строке файла OUTPUT.TXT записывается последовательность команд исполнителя (без пробелов).
Пример INPUT.TXT: OUTPUT.TXT для примера:
123456712 ++<+
12
808 Задача 3. Прямоугольники (45 баллов) ограничение времени: 1 сек на тест
На плоскости нарисовали красный прямоугольник. Затем нарисовали N (0 < N < 100) зеленых прямоугольников (зеленые прямоугольники могут пересекаться между собой, а также с красным прямоугольником). Стороны всех прямоугольников (как красного, так и зеленых) параллельны осям координат.
Требуется написать программу, строящую набор прямоугольников со сторонами, параллельными осям координат, такой чтобы выполнялись следующие условия:
• прямоугольники полностью покрывают часть красного прямоугольника, которая не покрыта зелеными прямоугольниками;
• прямоугольники не пересекаются между собой и с зелеными прямоугольниками (касаться сторонами они при этом могут),
• прямоугольники лежат внутри красного прямоугольника,
• количество прямоугольников в наборе не превышает величины (2N+1)2.
Входные данные
В первой строке входного файла INPUT.TXT содержатся 4 целых числа – координаты противоположных углов красного прямоугольника. Во второй строке задано число N. В каждой из последующих N строк располагаются четверки целых чисел, задающих координаты противоположных углов зеленых прямоугольников. Числа разделены пробелами.
Выходные данные
Выходной файл OUTPUT.TXT должен содержать в первой строке число М – количество прямоугольников в искомом наборе. В каждой из последующих М строк должны располагаться четверки целых чисел, задающих координаты противоположных углов прямоугольников. Числа в строках должны быть разделены пробелами.
Пример INPUT.TXT: один из вариантов OUTPUT.TXT для примера:
5 5 10 10 3
2 5 5 8 10
8 2 9 9 8 9 10 10
2 1 20 8 9 8 10 9
809 Задача 4. Палиндромы (45 баллов) ограничение времени: 2 сек на тест
Непустая строка называется палиндромом, если она одинаково читается как слева направо, так и справа налево. Пусть задана строка S, состоящая из N прописных букв латинского алфавита. Вычеркиванием из нее некоторых букв нужно получить палиндром.
Требуется написать программу, определяющую, сколько существует способов вычеркивания из заданной строки некоторого (возможно пустого) набора букв, чтобы оставшаяся строка была палиндромом. Способы, отличающиеся порядком вычеркивания символов, считаются одинаковыми.
Входные данные
В единственной строке входного файла INPUT.TXT записано N букв слова S (1 N 60).
Выходные данные
В единственной строке выходного файла OUTPUT.TXT должно содержаться найденное число способов.
Пример INPUT.TXT: OUTPUT.TXT для примера:
BAOBAB 22