Раздел 2 Лабораторная работа №5. Задания для лабораторной работы №5
Нелинейная регрессия общего вида
Даны данные для двух показателей Х и У. Исследовать их зависимость.
Вычислить коэффициенты регрессии, изобразить на графике фактические данные и результаты расчетов (для указанных в лабораторной работе №5 видов регрессии)
Х
0.1
0.12
0.11
0.14
0.16
0.21
0.18
0.22
0.25
У
0.1
0.3
0.2
0.4
0.6
0.3
0.8
0.9
0.9
Х
0.1
0.1
0.2
0.1
0.3
0.4
0.5
0.7
0.9
У
0.10
0.11
0.12
0.10
0.13
0.10
0.16
0.14
0.17
Х
0.14
0.16
0.13
0.17
0.12
0.18
0.19
0.25
0.28
У
0.31
0.34
0.32
0.35
0.37
0.41
0.38
0.45
0.50
Х
0.4
0.6
0.3
0.7
0.2
0.8
0.9
0.15
0.18
У
0.31
0.34
0.32
0.35
0.37
0.41
0.38
0.45
0.50
Х
0.4
0.6
0.3
0.7
0.2
0.8
0.9
0.15
0.18
У
0.21
0.24
0.22
0.25
0.27
0.31
0.28
0.35
0.40
Х
0.44
0.46
0.43
0.47
0.42
0.48
0.49
0.55
0.58
У
0.21
0.24
0.22
0.25
0.27
0.31
0.28
0.35
0.40
Х
0.44
0.46
0.43
0.47
0.42
0.48
0.49
0.55
0.58
У
0.1
0.4
0.2
0.5
0.7
0.3
0.8
0.5
0.9
Х
0.14
0.16
0.13
0.15
0.12
0.18
0.19
0.25
0.28
У
0.1
0.4
0.2
0.5
0.7
0.3
0.8
0.5
0.9
Х
0.14
0.16
0.13
0.15
0.12
0.18
0.19
0.25
0.28
У
0.21
0.24
0.22
0.25
0.27
0.23
0.28
0.25
0.29
-
Х
0.1
0.11
0.2
0.18
0.3
0.4
0.5
0.7
0.9
У
0.21
0.24
0.22
0.25
0.27
0.23
0.28
0.25
0.29
Нелинейная регрессия общего вида
Задача. Две величины x и y измеряются в одних и тех же экспериментах. Экспериментальные данные приведены в следующей таблице:
Требуется исследовать зависимость y(x):
1) написать уравнение регрессии одного из перечисленных ниже видов, вычислив соответствующие коэффициенты регрессии:
-
гиперболическая кривая;
-
кривая Гомперца;
-
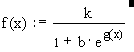логистическая кривая;
-
модифицированная экспонента;
-
экспоненциальная кривая;
-
логарифмическая парабола;
-
полиномиальная кривая;
2) построить линию регрессии и графики экспериментальных данных.
Решение.
1) Специальной переменной ORIGIN присваивают значение 1. Значением ORIGIN является номер первого элемента строки или столбца в матрице. По умолчанию ORIGIN=0.
В меню Math выбрать строку Options или
2) Введите результаты измерений величин x и y:
3) Выбрав функцию приближения
где a, b, c - искомые коэффициенты регрессии,
найдем частные производные этой функции по коэффициентам регрессии:
4) Введем вектор, элементами которого являются функция приближения и её производные, переобозначив коэффициенты регрессии u1=a, u2=b, u3=c:
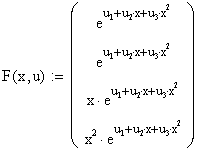
5) Введите вектор с начальными приближениями коэффициентов регрессии:
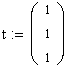
6) С помощью функции genfit(vx,vy,t,F), где vx и vy - векторы экспериментальных данных, t - вектор с начальными приближениями коэффициентов регрессии, F - вектор F(x,u), найдите значения коэффициентов регрессии a, b, c:
7) Подставляя
найденные значения коэффициентов
регрессии в первый элемент вектора
F(x,u), определите искомую функцию
приближения экспериментальных данных
(уравнение
регрессии), переобозначив r=x:
8) Постройте линию регрессии и графики экспериментальных данных. Для этого необходимо выполнить следующие действия:
щелкните по свободному месту в рабочем документе ниже уравнения регрессии, затем щелкните по кнопке декартова графика в панели графиков;
два раза подряд щелкните по полю графика, в появившемся диалоговом окне отметьте Crossed и Equal Scales, затем щелкните по кнопке Traces и для trace2 установите Types - points, Weight - 3, щелкните OK;
введите в позиции,
указанной меткой возле оси абцисс, имена
и
,
а возле оси ординат
и
,
границы графика должны включать все
экспериментальные значения;
график будет построен после щелчка вне поля графика.
