Лабораторная работа №4

Задачи теории вероятностей и математической статистики

 

Задача 1. Постройте биномиальное распределение для серии независимых испытаний с вероятностью успеха р=0.5, 0.7, 0.9. Постройте графики распределения и функции распределения. Проверьте равенство . Вычислите вероятность попадания значений случайной величины в интервал (1,6).

Решение:

1) Введите число независимых испытаний:

2) Введите вероятность успеха в одном испытании:

3) Определите интервал изменения значений случайной величины:

4) Определите распределения случайной величины по формуле Бернулли:

5) Постройте графики распределения:

6) Определите функции распределения:

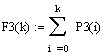
7) Постройте графики функций распределения:

8) Вычислите сумму всех значений вероятностей:

9) Вычислите вероятность попадания значений случайной величины в заданный интервал:

 

Задача 2. Провайдер обслуживает 1000 абонентов сети INTERNET. Вероятность того, что любой абонент захочет войти в сеть в течение часа, равна 0.002. Найти вероятность того, что в течение часа более 10 абонентов попытаются войти в сеть.

Решение:

1) Введите число n обслуживаемых абонентов:

2) Введите число к0 обслуживаемых абонентов в течение часа:

3) Введите вероятность p того, что любой абонент захочет войти в сеть в течение часа:

4) Определите вероятность того, что в течение часа ровно к0 абонентов попытается войти в сеть (формула Бернулли):

5) Определите вероятность того, что в течение часа менее к0 абонентов попытаются войти в сеть (функция распределения):

6) Определите требуюмую вероятность:

7) Определите требуюмую вероятность, используя приближенную формулу Пуассона:

8) Сравните полученные результаты.

9) Повторите все вычисления для n=40 и р=0.2, изменив в пунктах 1) и 3) соответствующие значения. Сравните.

 

Задача 3. Постройте графики плотности нормального распределения и функции нормального распределения N(0,1) (стандартное нормальное распределение).

Решение:

1) Введите значения параметров распределения N(a,?), где а - математическое ожидание, ? - среднее квадратическое отклонение случайной величины:

2) Определите плотность стандартного нормального распределения и постройте график:

3) Определите функцию распределения и постройте график:

 

Задача 4. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины ????распределенной равномерно на интервале (2,8).

Решение:

1) Введите концы интервала (a,b):

2) Определите плотность равномерного распределения:

3) Определите математическое ожидание:

4) Определите дисперсию:

5) Определите среднее квадратическое отклонение:

 

Задача 5. Сгенерируйте выборку 250 значений случайной величины, имеющей нормальное распределение N(150,10). Вычислите максимальное, минимальное значения выборки и размах выборки. Выполните группировку (10 одинаковых интервалов), постройте соответствующие гистограмму, полигон частот.

Решение:

1) Установите в меню Math режим Optimization.

2) Введите объем выборки n:

3) Сгенерируйте выборку объема n значений случайной величины ?? имеющей нормальное распределение N(a,b) с помощью функции rnorm(n,a,b), значением которой является вектор, содержащий n выборочных значений нормально распределенной величины с математическим ожиданием а и средним квадратическим отклонением b.

4) Упорядочите выборку по возрастанию (вариационный ряд):

5) Вычислите максимальное, минимальное значения и размах выборки:

6) Определите число интервалов группировки m и их длину ?:

7) Определите середины интервалов группировки:

8) Постройте гистограмму и полигон частот с помощью функции hist(x,?), где х - вектор середин интервалов группировки, ? - выборка. При построении гистограммы в окне настройки изображения графиков пометьте Crossed в пункте X-Y-Axes и установите тип линии bar в пункие Traces.

9) Повторите все вычисления для m=20 и m=100, изменяя соответствующие значение в пункте 6).

10) Повторите все вычисления выборки объема n=300 и m=50, изменяя соответствующие значение в пунктах 2) и 6).