Тема 8. Решение обыкновенных дифференциальных уравнений.

Содержание лекции	Содержание лабораторной работы
Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Рунге-Кутта. Многошаговые методы. Решение краевой задачи для линейного 2-ого порядка сведением к разностной краевой задаче. Метод прогонки. Численное решение обыкновенных дифференциальных уравнений на ЭВМ.	Постановка задачи. Решение дифференциального уравнения методом Коши, методом Эйлера, Методом Эйлера-Коши, Рунге-Кутта 4-го порядка и Адамса.

Задание

Решить задачу Коши для дифференциального уравнения y=f(x,y) на отрезке [a,b] при заданном начальном условии и шаге интегрирования h.

Номер варианта соответствует порядковому номеру в списке.

Исполнение: С помощью инструментальных пакетов MS Office, MathCad методами Эйлера, Рунге-Кутта 4-го порядка и Адамса, предусмотрев вывод полученных решений в виде таблиц и графиков.

Лабораторная установка: Персональный компьютер с ОС Windows, MS Office, MathCad.

Оценка: Сопоставление полученных результатов, решаемых различными методами

Время выполнения работы: 5 часов.

Методические указания

Дана система дифференциальных уравнений:

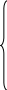, где n – размерность системы.

Рассмотрим задачу Коши для данной системы. Пусть известны начальные условия при x₀ = a: y₁(x₀) = y₁₀, y₂(x₀) = y₂₀, …, y_n(x₀) = y_n0. Требуется найти y₁(x), y₂(x),…, y_n(x), проходящие через заданные точки: (x₀,y₁₀), (x₀,y₂₀), …, (x₀,y_n0).

Методы решения одного дифференциального уравнения можно обобщить и на их системы.

Метод Рунге-Кутта 4-го порядка для системы ОДУ 1-го порядка

Расчетные формулы метода Рунге-Кутта 4-го порядка для системы ОДУ 1-го порядка:

где ;

;

;

m – количество узлов;

– номер функции;

– номер узла;

;

;

;

.

Контрольные вопросы и задания

1. Задать исходные данные: функцию f правой части, начальное значение .

2. Используя функцию eyler (см. ПРИЛОЖЕНИЕ 7.B), найти приближенное решение задачи Коши с шагом h=0.1 по явному методу Эйлера.

3. Используя встроенную функцию rkfixed пакета MATHCAD, найти приближенное решение задачи Коши с шагом h=0.1 по методу Рунге-Кутты 4 порядка точности (см. ПРИЛОЖЕНИЕ 7.B).

4. Найти решение задачи Коши аналитически.

5. Построить таблицы значений приближенных и точного решений. На одном чертеже построить графики приближенных и точного решений.

6. Оценить погрешность приближенных решений двумя способами:

a) по формуле ; здесь и - значения точного и приближенного решений в узлах сетки , i=1,..N;

b) по правилу Рунге (по правилу двойного пересчета) (см. ПРИЛОЖЕНИЕ 7.C).

7. Выяснить, при каком значении шага h=h* решение, полученное по методу Эйлера, будет иметь такую же погрешность (см. п. 6а), как решение, полученное с помощью метода Рунге-Кутты с шагом h=0.1.

УКАЗАНИЕ. В п. 7 рекомендуется провести серию вычислений решения по методу Эйлера, дробя шаг h пополам.

N	f(t,y)	t0	T	y0	N	f(t,y)	t0	T	y0
1		1	2	0	14		1	2	1
2			+1	0	15		1	2	3
3		0	1	0	16		1	2	1
4			+1	0.5	17		1	2	1
5		-1	0	1.5	18		1	2
6		0	1	1	19		1	1	1
7			+1	1	20		0	1	3
8			+1		21		0	1	1
9		1	2	1	22		0	1	1
10		0	1		23		0	1	0.5
11		2	3	4	24		0	1	3
12		1	2		25		0	1	-0.5
13		1	2	1	26		1	2	1

УЧЕБНО-МЕТОДИЧЕСКИЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

Основная литература

1. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике, Ч. 2. – М.: Финансы и статистика, 1999.

2. Бахвалов Н.С.., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях - М.: Высшая школа , 2000.

3. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения – М.: Высшая школа , 2001.

4. Денежкина И.Е., Посашков С.А., Шандра И.Г. Дифференциальные уравнения – М.: Изд-во ФА, 2002.

5. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения): Учеб. пособия для вузов. - М.: Высш. шк., 2000. - 266 с: ил.

6. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: учебное пособие для вузов. – М.: Наука, 1987.

7. Уотшем Т.Дж., Паррамоу К. Количественные методы в финансах. – М.: ЮНИТИ, 1999 (рекомендовано Министерством образования РФ).

8. Красс М.С. Математика для экономических специальностей. Учебник. – М.: ИНФРА-М, 1999 (рекомендовано Министерством образования РФ).

9. Киреев В.М., Пантелеев А.В. Численные методы в примерах и задачах – М.: Изд-во МАИ, 2000.

10. Ракитин В.И., Первушин В.Е. Практическое руководство по методам вычислений с приложением программ для персональных компьютеров: Учеб.пособие. М.: Высш.шк., 1998. - 383 с.

Дополнительная литература

1. Березин И.С., Жидков Н.П. Методы вычислений. В 2-х ч. – М.: Физматгиз, 1962.

2. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учеб. пособие. - М.: Финансы и статистика, 1999.

3. Волков Е.А. Численные методы. - М.: Наука, 1982.

4. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике.- М.: Высш. шк., 1990

5. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа.- М.: Наука, 1967

6. Демидович Б.Н., Марон И.А. Основы вычислительной математики.- М.: Наука, 1970.

7. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы.- М.: Просвещение, 1991

8. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн функций .- М.: Наука, 1980.

9. Калиткин Н.П. Численные методы.- М.: Наука, 1978.

10. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах.- М.: Наука, 1972.

11. Лапчик М.П., Рагулина М.И., Стукалов В.А. Численные методы: Учеб. пособие для пед. вузов.-М.: Академия, 2001.

12. Марчук Г.И. Методы вычислительной математики.- М.: Наука, 1989.

13. Ракитин В.И., Первушкин В.Е. Практическое руководство по методам вычислений с приложением программ для персональных компьютеров: Учеб. пособие.- М.: Высш. шк., 1998.

14. Самарский А.А., Гулин А.В. Численные методы.- М.: Наука, 1989.

15. Сборник задач по методам вычислений: Учеб. пособие: Для вузов/Под ред. П.И. Монастырного .- М.: Физматлит, 1994.

16. Хемминг Р.В. Численные методы для научных работников и инженеров.

17. Амосов А., Дубинский Ю. А., Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. – М.: Высш. шк., 1994.

18. Волков Е. А. Численные методы. – М.: Наука, 1987.

19. Дьяконов В. П. Математическая система Maple V R3/R4/R5. – М.: Изд-во "СОЛОН", 1998.

20. Калиткин Н.Н. Численные методы. – М.: Наука, 1978.

21. Копченова Н.В., Марон И. А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972.

22. Пирумов У.Г. Численные методы.: Учебное пособие. – М.: Изд-во МАИ, 1998.