Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Инженерно-технологическая академия ЮФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

pos_ms_pr.doc

Скачиваний:

Добавлен:

01.04.2025

Размер:

6.84 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 279 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

2. Нечеткие множества

2.1. Определение нечеткого множества

Решая задачи, приходится встречаться с ситуациями, когда элемент в некоторой степени принадлежит данному множеству. Например, определяется множество небольших величин. Кто может точно сказать, начиная с какого значения величины можно считать величину небольшой? На этот вопрос нет однозначного ответа. Поэтому одним из способов математического описания нечеткого множества является определение степени принадлежности элемента нечеткому множеству. Степень принадлежности задается числом из интервала [0,1]. Границы интервала - 0, 1, означают, соответственно, «не принадлежит» и «принадлежит». В разд. 1 принадлежность элемента x множеству А записывается в формализованном виде xА. Данная запись может быть представлена в виде характеристической функции:

Принадлежность множеству может быть представлена в графической виде. Например, в одномерном арифметическом пространстве R заданы два множества AR и BR. Принадлежность xА можно представить в виде прямоугольника П_А, показанного на рис. 2.1, а принадлежность xВ - в виде прямоугольника П_В, показанного на рис. 2.2. Принадлежность x объединению множеств xАВ представлена прямоугольником П_А__В, показанны на рис. 2.3. Принадлежность двухмерному множеству будет представлена параллепипедом в трехмерном пространстве, а принадлежность n–мерному множеству – (n+1)-мерным параллепипедом.

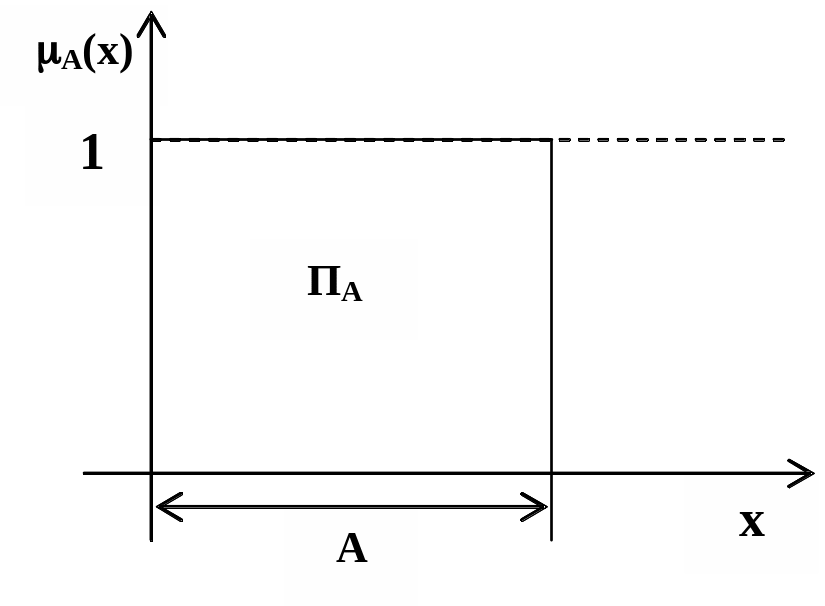
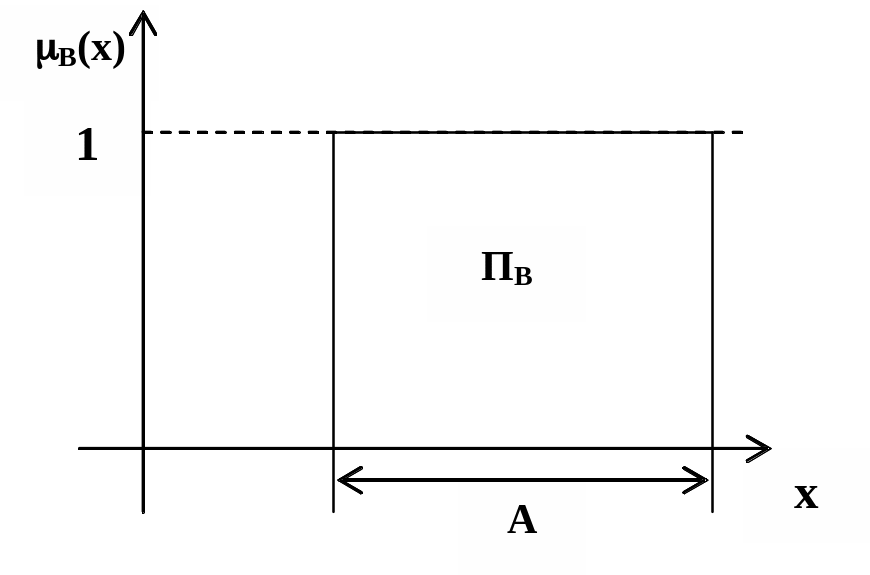
Рис. 2.1 Рис. 2.2

Нечетким подмножеством A множества X называется множество двоек [2 - 4]. Функция _A, являющаяся отражением элементов xX в элементы множества [0,1] (_a:X[0,1]), называется функцией принадлежности нечеткого множества , а X - базовым множеством.

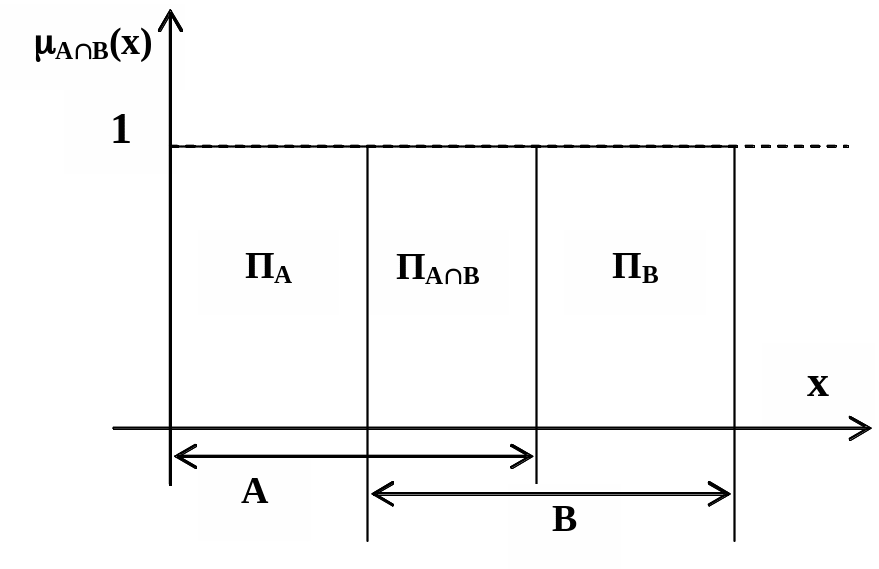
Рис. 2.3

Конкретное значение _A(x), заданное для элемента x, называется степенью принадлежности элемента x нечеткому множеству . Hосителем нечеткого множества называется подмножество X, содержащее те элементы xX, для которых значение функции принадлежности больше нуля.

Пример. Пусть X - множество натуральных чисел X={1,2,3, ...,x_max}, предназначенных для определения цены изделия. Нечеткое подмножество «небольшая цена» может быть задано в следующем виде:

={<1/1>,<0,9/2>,<0,8/3>,<0,7/4>,<0,6/5>,<0,5/6>,<0,4/7>,<0,3/8>,

<0,2/9>,<0,1/10>,<0/11>,...,<0/x_max>}.

Принадлежность значений цены нечеткому подмножеству «небольшая цена» показана на рис .2.4.

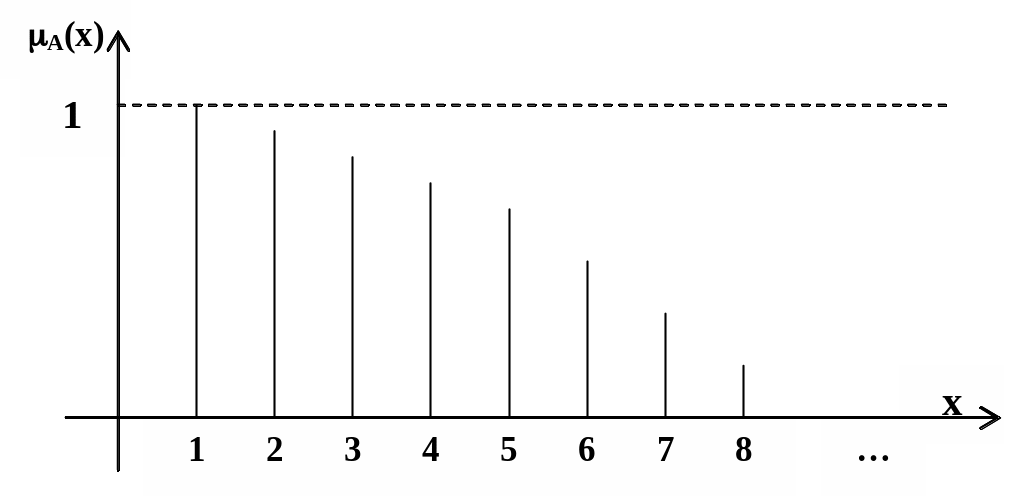
Рис. 2.4

Если рассматривать множество X как непрерывное множество натуральных чисел, то принадлежность значений цены нечеткому подмножеству «небольшая цена» будет иметь вид непрерывной функции, как показано на рис .2.5. Рассмотрим свойства нечетких множеств.

Высота (height - hgt) нечеткого множества : .

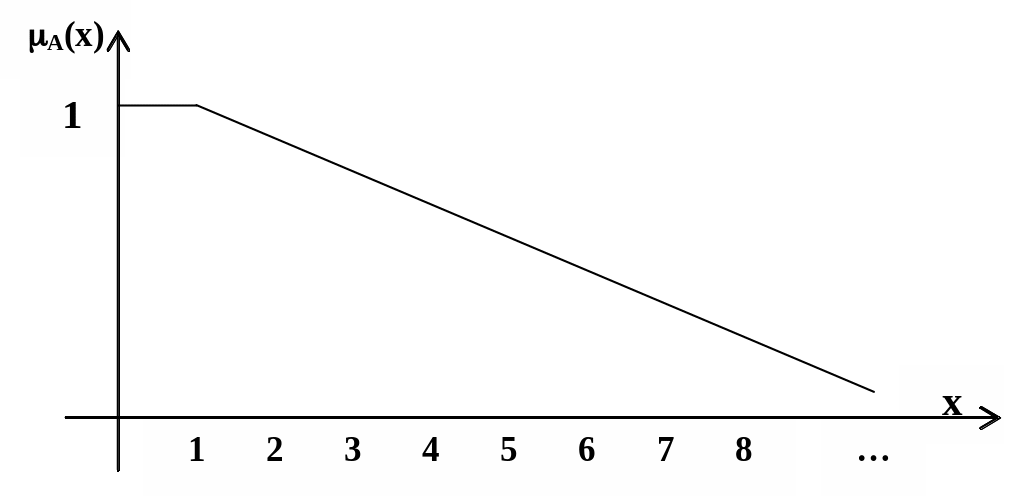
Рис. 2.5

Нечеткое множество с hgtA=1 называется нормальным, а при hgtA<1 - субнормальным. Ядро (core, kernal, nucleus) или центр нечеткого множества : core ={xX/_A(x)=1}. Основание (support – supp) нечеткого множества : supp ={xX/_A(x)>1}. Поперечными точками (crossover point) нечеткого множества называется совокупность core {xX/_A(x)=0,5}. Уровень , или –разрез (сечение) нечеткого множества : _={xX/_A(x)}. –разрез нечеткого множества еще обозначают: -cut . Строгий –разрез нечеткого множества : _={xX/_A(x)>}. Выпуклое (convex) нечеткое множество : x₁,x₂,x₃X:x₁x₂x₃_A(x₂)min(_A(x₁),_A(x₃)). При невыполнении неравенства нечеткое множество называется невыпуклым. На рис. 2.6 приведена иллюстрация вышеназванных свойств.

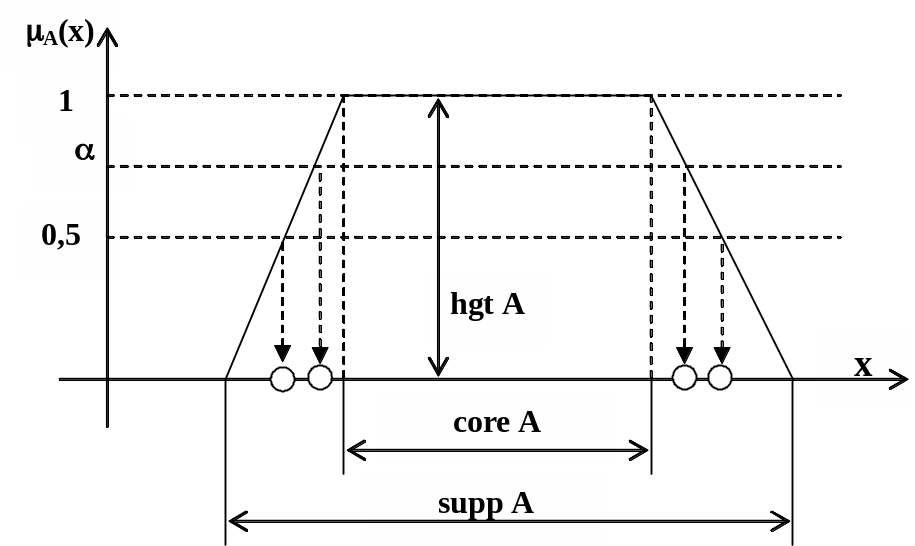
Рис. 2.6

Отдельным видом нечеткого множества А является нечеткое число (нечеткий синглтон) при выполнении условий [6]: А является выпуклым, высота является нормальной (hgt А=1), _А(x) является кусочно-непрерывной функцией, ядро или центр множества A (core A) содержит одну точку. Пример принадлежности x нечеткому числу «приблизительно 5» показан на рис. 2.7.

Другим видом нечеткого множества является задание некоторых переменных в виде нечеткого интервала. Известно [10] определение.

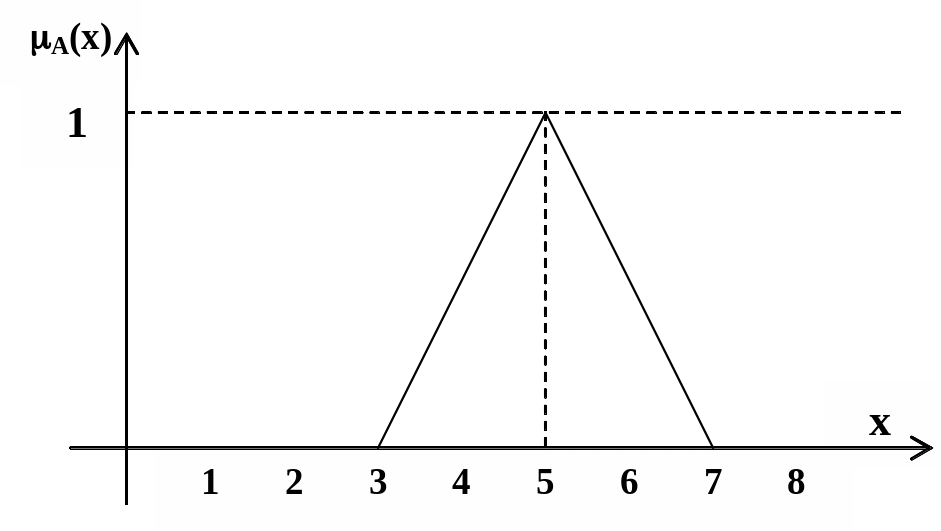
Рис. 2.7

Нечеткий интервал – это выпуклая нечеткая величина A, функция принадлежности которой квазивогнута, так что

u,v, w[u,v], _A(w)min(_A(u), _A(v)), u,v,wX.

Тогда нечеткое число - полунепрерывный сверху нечеткий интервал с компактным носителем и единственным модальным значением. Задание параметров задачи в виде нечеткого интервала – это очень удобная форма для формализации неточных величин. Обычный интервал часто является неудовлетворительным представлением, т.к. необходимо фиксировать его границы. Могут быть оценки завышенными или заниженными, что вызовет сомнение в результатах расчетов. Задание параметров задачи в виде нечеткого интервала будет одновременно и завышенным, и заниженным, а носитель (базовое множество) нечеткого интервала будут выбран так, что ядро содержит наиболее правдоподобные значения и будет гарантировано нахождение рассматриваемого параметра в требуемых пределах.

Задание нечетких интервалов может быть осуществлено экспертами следующим образом. Нечеткий интервал задают четверкой параметров М=( ) (см. рис.2.8), где и - соответственно нижнее и верхнее модальные значения нечеткого интервала, а  и  представляют собой левый и правый коэффициент нечеткости. Задание нечеткого интервала может быть выполнено следующими способами.

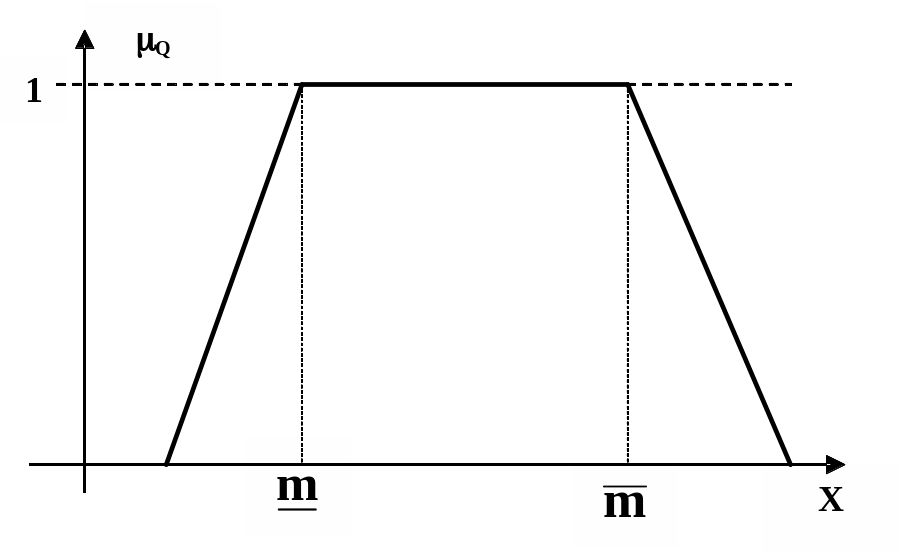
Рис. 2.8

Вариант 1. Нижнее и верхнее модальные значения интервала совпадают, а  и  равны нулю. Значение x определяется с неопределенностью равной нулю. Для задания нечеткой входной переменной на множестве X определим формально нечеткий интервал =(x_min=x, x_m_ax=x,0,0), где x_imin - нижнее модальное значение , а x_m_ax- верхнее модальное значение .

Четкое задание x на множестве значений X, как это показано на рис. 2.9, является частным случаем задания нечеткого интервала, причем, _A(x) - значение степени принадлежности интервалу.

Вариант 2. Задание x определяется с неопределенностью отличной от нуля. Пример показан на рис. 2.10. Нечеткий интервал определен, как =(x_min, x_m_ax=x_min,0,), т.е. верхнее и нижнее модальные значения интервала совпадают.

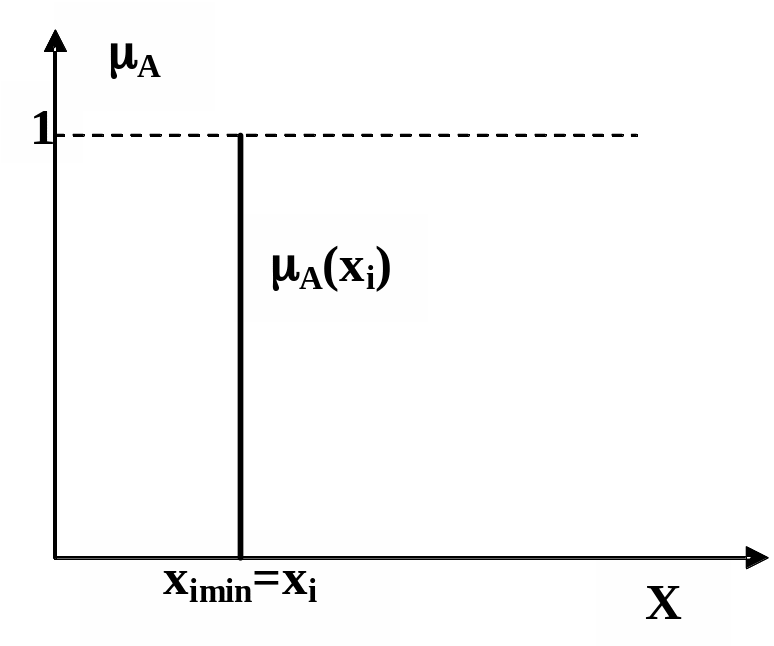
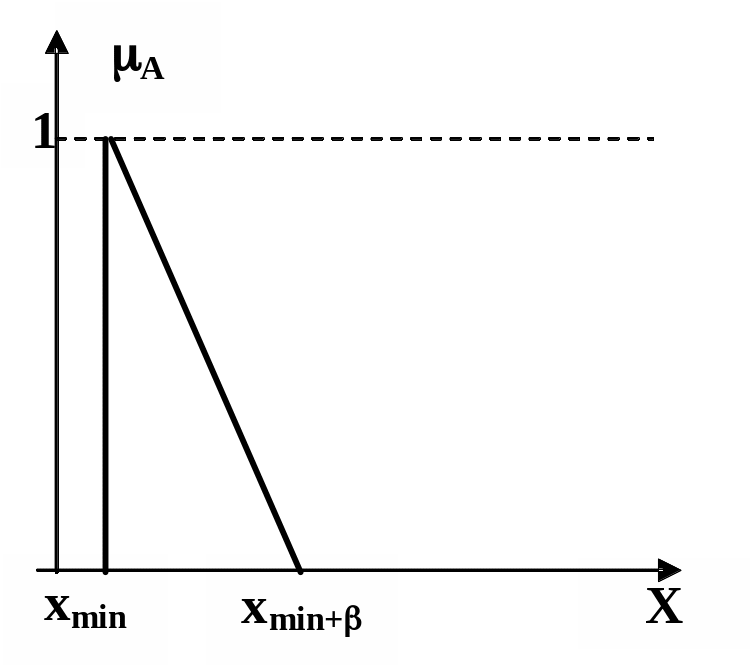
Рис. 2.9 Рис. 2.10

Вариант 3. Задание x может быть получено из интервала [А,В]. Пример показан на рис. 2.11. Степень принадлежности равна единице, причем =(А=x_min,В=x_m_ax,0,0), где А – нижнее модальное значение (минимально возможное значение входной переменной x), В – верхнее модальное значение (максимальное значение входной переменной x.

Вариант 4. Значение входной переменной x_i может быть получено из интервала значений [А,С] таким образом, что в интервале [А,В] неопределенность получения равна единице (ABС). Формально нечеткий интервал определен в виде =(А=x_min,В=x_max,0,). Пример задания показан на рис. 2.12, где =С-В.

Вариант 5. Значение входной переменной q_i экспертами может быть определено из интервала значений [А,D] таким образом, что в интервале [В,C] неопределенность получения равна единице (ABСD). Формально нечеткий интервал в этом случае определим в виде =(B=x_min,C=x_max,,). Пример задания нечеткого интервала показан на рис. 2.13, где =B-A, =D-C.

Рассмотрим операции над нечеткими интервалами.

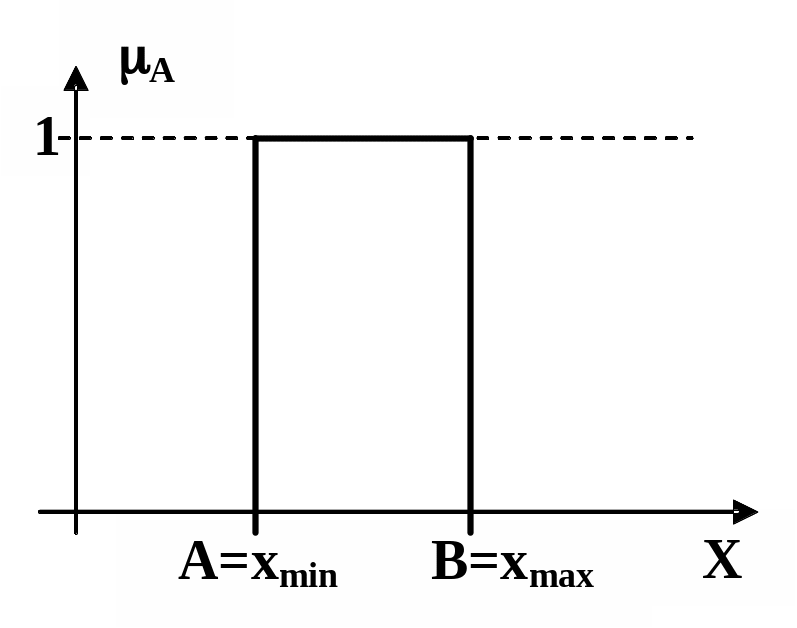
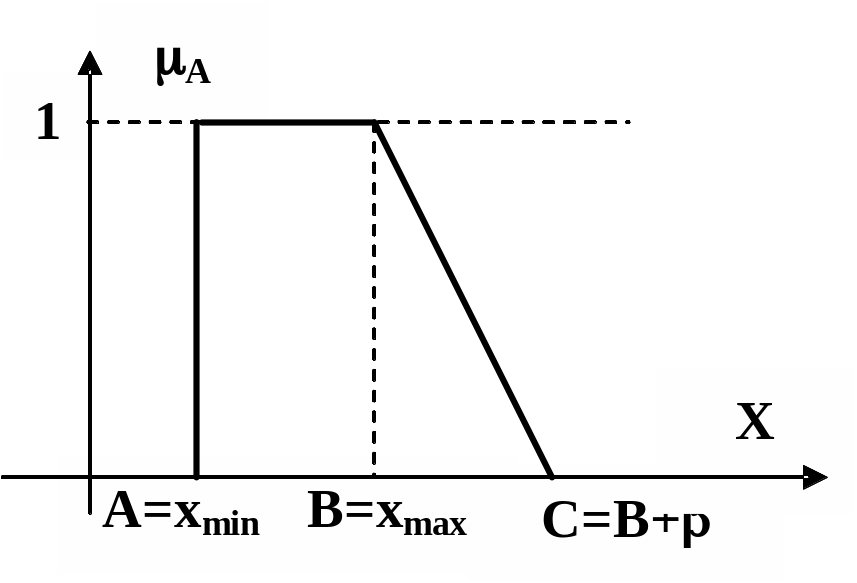
Рис. 2.11 Рис. 2.12

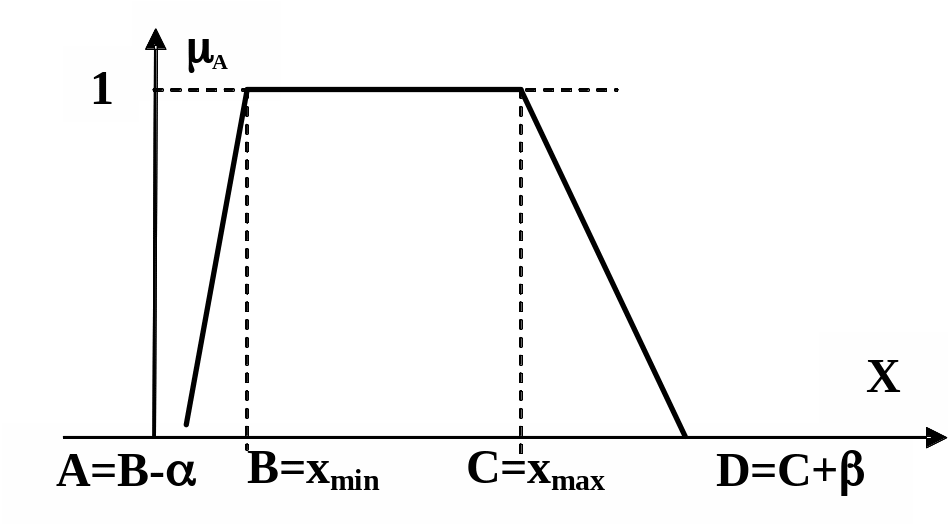
Рис. 2.13

Операция нечеткого суммирования для нечетких интервалов определяется следующим образом. Сумма двух нечетких интервалов М_i=( ) и М_j=( ), записываемая в виде М_i М_j, также есть нечеткий интервал М_i М_j= [11], где =_i + _j; =_i + _j; , . Сумма n нечетких интервалов определится формулами:

Если , a , где и - выпуклые интервалы, то , причем - совокупность интервалов, которая определена по предыдущим формулам.

Операция разности нечетких интервалов определяется следующим образом. Нечеткая разность двух нечетких интервалов и есть трапециевидный интервал , для которого =|-|, =|-|, , , где - соответственно нижние модальные значения нечетких интервалов , - верхние модальные значения нечетких интервалов .

Принятие решений связано с осуществлением сравнений полученного нечеткого интервала либо экспертами, либо по данным моделирования с действительным числом. Операция сравнения нечеткого интервала и действительного числа выполняется следующим образом.

Действительное число А представим в виде интервала (А,А,0,0). Определение меньшего или большего значения нечеткого интервала по отношению к действительному числу А производится по формулам:

А, если |A-( )||A-( )| и A ;

А, если |A-( )||A-( )| и A .

Для нечетких интервалов существует операция произведения и деления. Произведение двух нечетких интервалов и определится в виде трапециевидного интервала , параметры которого определяют по формулам: