1.8. Отображение как функция

1.8.1. Функция. Отображение f: XY называется функцией, если оно является однозначным, т.е. для любых пар (x₁,y₁)f и (x₂,y₂)f, если х₁=х₂, следует y₁=y₂. Однозначное соответствие q=(X,Y,f) в этом случае называется функциональным, т.е. в графике f не может быть двух пар вида (x,y₁) и (x,y₂), y₁y₂, xX, y₁,y₂Y. Если существует такой элемент xX, образ которого содержит более одного элемента yY, то соответствие называется нефункциональным. Если же для любого элемента xX образ f(x) содержит более одного элемента yY, то соответствие называется антифункциональным. На рис. 1.13 приведены графические задания функционального, нефункционального и антифункционального соответствий.

*

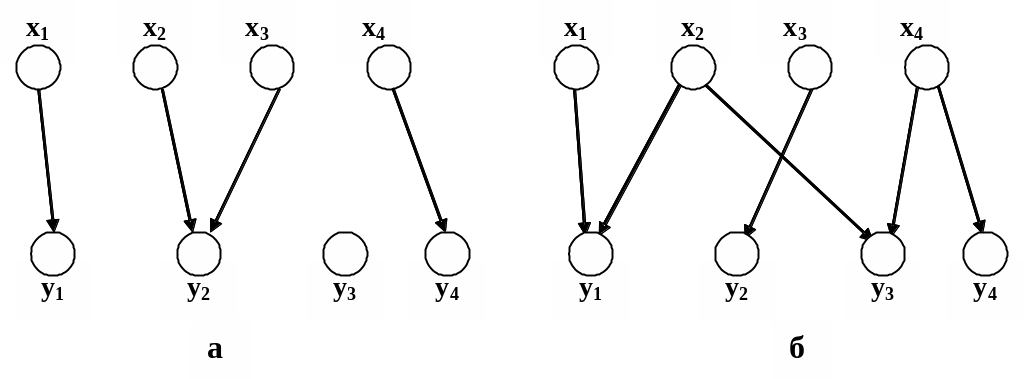
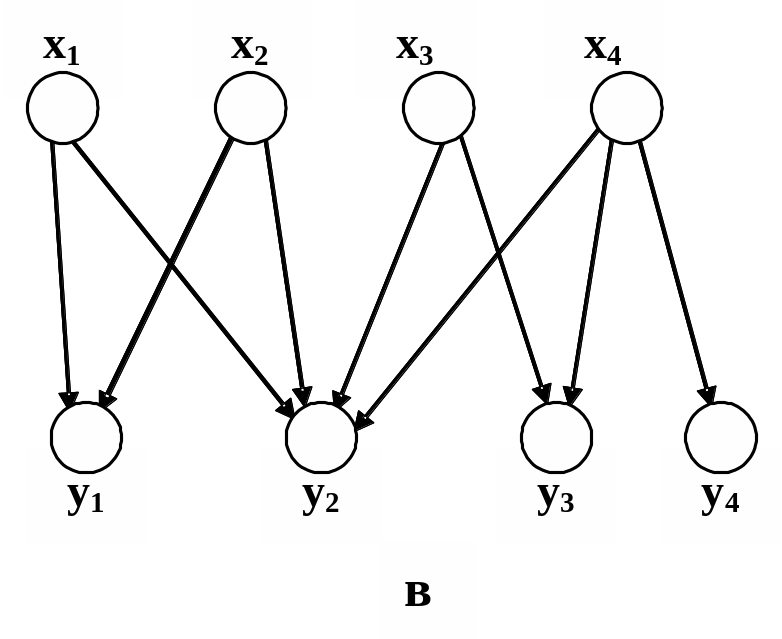
а – функциональное, б – нефункциональное, в – антифункциональное.

Рис. 1.13

Значение y в любой из пар (x,y)f называется функцией от данного х и записывается в виде логической формулы y=f(x). Формально функция определена: f={(x, y)XYy=f(x)}.

Говорят, что функция f отображает элемент xX в элемент yY; х – аргумент функции, y – значение функции на аргументе х; f – есть множество, элементами которого являются пары (x, y), участвующие в соответствии q=(X, Y, f).

Исходя из определения функции, рассмотрим способы ее задания. Если Х есть конечное множество небольшой мощности, то возможно задание функции перечислением всех пар (x, y), которые составляют множество f. Если Х и Y есть множество вещественных или комплексных чисел, то под f(x) понимается математическая формула. Например, если X=Y= - пространство действительных чисел, f={(x, y)²y=x²}, то тогда f(x)=x².

Может рассматриваться случай, когда на некоторых Ai ( ) подмножествах множества Х (A_iX, ) при определении соответствия в виде функции приходится пользоваться различными математическими формулами f_i(x), . Т.е. функция f(x) будет определена в виде

.

Например, релейная функция имеет вид

.

Функция y=f(x)=x задается в виде выражения

Множество пар (x,y)f можно также изобразить в виде точек на плоскости ₂. В этом случае получим график функции. Если в выражении f: XY множество Х=UV, то соответствие f: XY есть функция f(u,v) от двух переменных uU и vV, или формально записывается в виде

f={(u, v, y)UVYy=f(u, v)}.

Можно определить в общем случае функцию от n числа переменных.

Существует операция сужения функции. Если f: XY – некоторая произвольная функция и АХ – произвольное множество, то сужением функции f на множестве А называется функция f_А, содержащая пары (x,y)f, в которых хА, а следовательно (x,y)AY. Формально сужение функции определится выражением: f_A=f(AY). Сужение функции возможно, например, при табличном задании функции, определенной на бесконечном множестве Х.

Так как соответствию q=(X,Y,Q) можно сопоставить обратное соответствие q^-1=(Y,X,Q^-1), то и функции f: XY можно сопоставить обратную функцию (отображение) f-1: YX. Условия получения обратной функции для отображения f: XY следующие. Отображение f: XY должно быть однозначным, т.е. для любых (x₁,y₁)f и (x₂,y₂)f из х₁=х₂ следует y₁=y₂. Отображение f: XY должно быть и взаимооднозначным, т.е. из условия х₁х₂ следует y₁y₂. При выполнении этих условий обратное отображение f^-1: YX также является однозначным и определяет функцию x=f^-1(y), называемую обратной по отношению к функции y=f(x).

1.8.2. Функция времени. Если в качестве множества Х функции взять множество моментов времени Т, а в качестве Y взять множество вещественных чисел , то получим отображение, называемое функцией времени f:T. Время имеет одно направление, поэтому Т есть упорядоченное множество. Элементами функции являются двойки (t,x) или x(t), где tT, x. Каждая такая пара задает значение функции в момент времени t и определяет мгновенное значение функции. Полная совокупность двоек (t,x) представляет собой функцию времени. Примером функции времени является синусоида: f={(t,x)T x=Asin(t+)}.

Время является величиной бесконечной, поэтому на практике обычно рассматривают функцию, заданную на временных интервалах.

Сужение функции x(t), заданной на бесконечном интервале -<t<, на конечный интервал (t₁,t₂] называется отрезком функции x(t) и обозначается х(t₁,t₂], т.е. х(t₁,t₂]={x(t)t(t₁,t₂]}. Если множество Т представляет собой множество натуральных чисел, то функция f:T называется функцией с дискретным временем. Элементы множества Т обозначаются через n (nT), так что двойка (n,x), обозначаемая также x[n] или x_n, определяет значение функции в момент n.

1.8.3. Функционал. Пусть в отображении f: XY множество Х есть множество функций F(x), а Y – множество вещественных чисел. В частности, пусть Y есть множество моментов времени. В этом случае приходим к отображению, называемому функционалом и формально записываемому выражением J: F(x)T.

Понятие функционала поясним на примере. Известно, что если производить подключение питания к некоторой схеме, то в схеме протекают переходные процессы, определяемые параметрами схемы и поданным напряжением. На рис. 1.14 показан пример возможных протеканий переходного процесса. В зависимости от параметров функции f(x) время t установления переходного процесса различное.

Если множество функций f(x) обозначим через F(x), а через Т – множество вещественных чисел t, которые определяют время установления переходного режима, то зависимость времени протекания переходного режима записывается как отображение J: F(x)T.

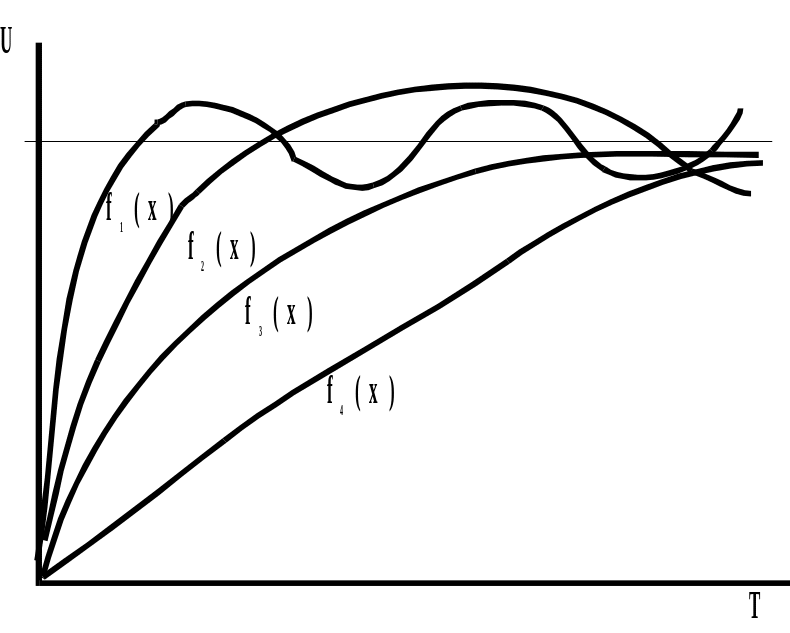
Рис. 1.14

Всевозможные пары (f(x),t) есть элементы множества J, причем f(x)F(x), tT. Говорят, что вещественное число tT представляет собой функционал J от функции f(x)F(x) или формально: t=J[f(x)].

В задачах теории автоматического регулирования определяется оптимальная функция f(x), которой соответствует минимальное время t установления переходного процесса для выходной величины. Требуется выполнить условие , при котором t будет минимальной величиной t_мин. Говоря языком теории множеств, необходимо сопоставить t_мин с некоторой функцией fi(x)F(x).

1.8.4. Оператор. Если в отображении f: XY множества Х и Y являются множествами функций с элементами x(t)X и y(t)Y, то данное отображение называется оператором и обозначается L: XY. Элементами множества L будут всевозможные пары (x(t),y(t)). Оператор L преобразует функцию x(t) в функцию y(t) и поэтому y(t)=L[x(t)]. В математике известны операторы:

- дифференцирования fⁱ(x)=P[f^i-1(x)], i1, что имеет запись в математическом анализе fⁱ(x)=df^i-1(x)/dx;

- интегрирования f(x)=(x)/p, что соотвествует записи ;

а также много других операторов.

В системах автоматического управления оператором преобразования управляющей величины x(t) в управляемую величину y(t) можно рассматривать передаточную функцию системы.