1.6. Соответствия
Если существует способ (закон) сопоставления элементов хХ с элементами yY так, что имеется возможность образования двоек (x,y), причем для каждого элемента хХ возможно указать элемент yY, с которым сопоставляется элемент х, то говорят, что между множествами Х и Y установлено соответствие. В сопоставлении могут участвовать не все элементы Х и Y. Для задания соответствия необходимо указать:
- множество Х, элементы которого сопоставляются с элементами другого множества;
- множество Y, с элементами которого сопоставляются элементы множества Х;
- множество QХY, определяющее закон, согласно которому осуществляется соответствие, т.е. перечисляющее все пары (x,y), участвующие в сопоставлении.
Соответствие, обозначаемое через q, представляет собой тройку множеств q=(X,Y,Q), где: X – область отправления соответствия, Y – область прибытия соответствия, Q – график соответствия, QХY. Очевидно, что Пр1QХ, а Пр2QY, причем множество Пр1Q называется областью определения соответствия, а Пр2Q – областью значений соответствия. Способы задания соответствий следующие.
При
теоретико-множественном задании
определяют множества Х={x1,
x2,…, xn}, Y={y1,
y2,…,ym}
и график Q={(xi,yj)},
хХ,
yY
,
При матричном способе задания соответствие задается в виде матрицы инцидентности RQ, которая имеет вид прямоугольной таблицы размером nm. Элементы хiХ соответствуют строкам матрицы RQ, а элементы yjY соответствуют столбцам. На пересечении хi строки и yj столбца ставится элемент rij=1, если элемент (xi,yj)Q, и rij=0, если (xi,yj)Q.
При графическом способе соответствие задается в виде рисунка (см. рис. 1.7.), на котором элементы хiХ – кружки одной линии, элементы yjY – кружки другой линии, а каждая двойка (xi,yj)Q обозначается стрелкой, идущей от кружка xi к кружку yj. Такое представление называется графиком.
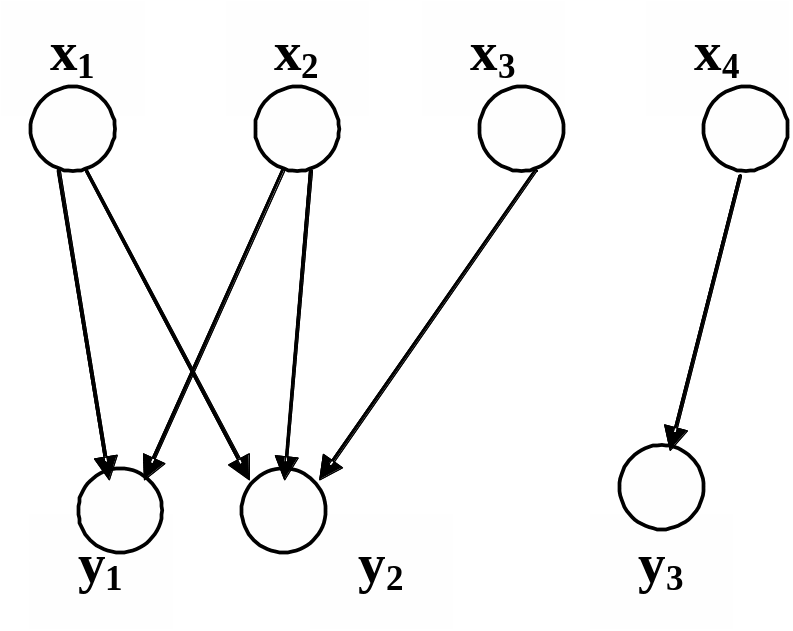
Х={x1,x2,x3,x4}, Y={y1,y2,y3}, Q={(x1,y1), (x1,y2), (x2,y1), (x2,y2), (x3,y2), (x4,y3)}.
Рис. 1.7
Если будем сопоставлять для множества элементов yY элементы из множества Х, то получим соответствие q-1=(Y,X,Q-1), обратное соответствие q (инверсия соответствия q).
Композиция (лат. compositio – сочинение, составление) соответствий - последовательное применение двух и более соответствий. Композиция двух соответствий есть операции с тремя множествами, на которых определены два соответствия:
Q=(X,Y,Q), QXY, p=(Y,Z,P), PYZ.
Соответствие
q определяет для
некоторого элемента хХ
некоторый (один или более) элемент yY,
а соответствие p для
некоторого элемента yY
определяет некоторый элемент zZ.
Композиция
соответствий q(p)
сопоставляет каждому элементу xX=Пр1Q
(области определения соответствия q)
один или более элементов zZ=Пр2P
(области значений соответствия p).
Композиция соответствий задается
выражением
q(p)=(X,Z,Q
P).
Пример графического задания композиции приведен на рис. 1.8 и рис. 1.9.
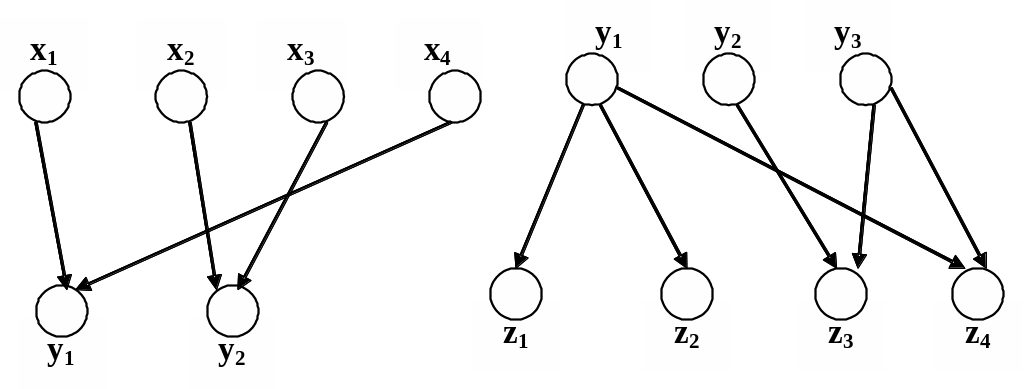
q={(x1,x2,x3,x4), (y1,y2), (x1,y1), (x2, y2), (x3,y2), (x4,y1)},
p={(y1,y2,y3), (z1,z2,z3,z4), (y1,z1), (y1,z2), (y1,z4), (y2,z3), (y3,z3), (y3,z4)}
Рис. 1.8
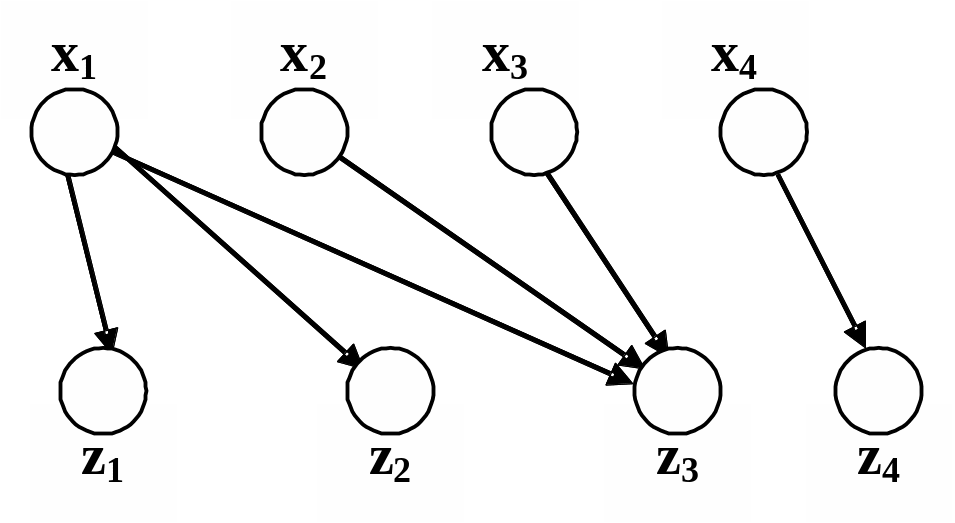
q(p)={(x1,x2,x3,x4), (z1,z2,z3,z4), (x1,z1), (x1,z2), (x1,z4), (x2,z3), (x3,z3), (x4,z4)}
Рис. 1.9
Пример графического задания операций объединения и пересечения соответствий приведен на рис. 1.10 – рис.1.12.
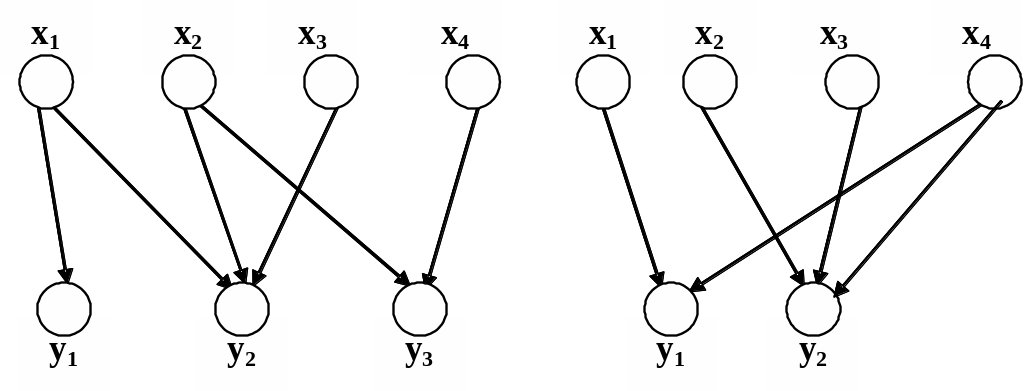q={(x1,x2,x3,x4),
(y1,y2,y3),
(x1,y1),
(x1,y2),
(x2,y2),
(x2,y3),
(x3,y2),
(x4,y3)},
p={(x1,x2,x3,x4),
(y1,y2),
(x1,y1),
(x2,y2),
(x3,y2),
(x4,y1),
(x4,
y2)}.
Рис. 1.10
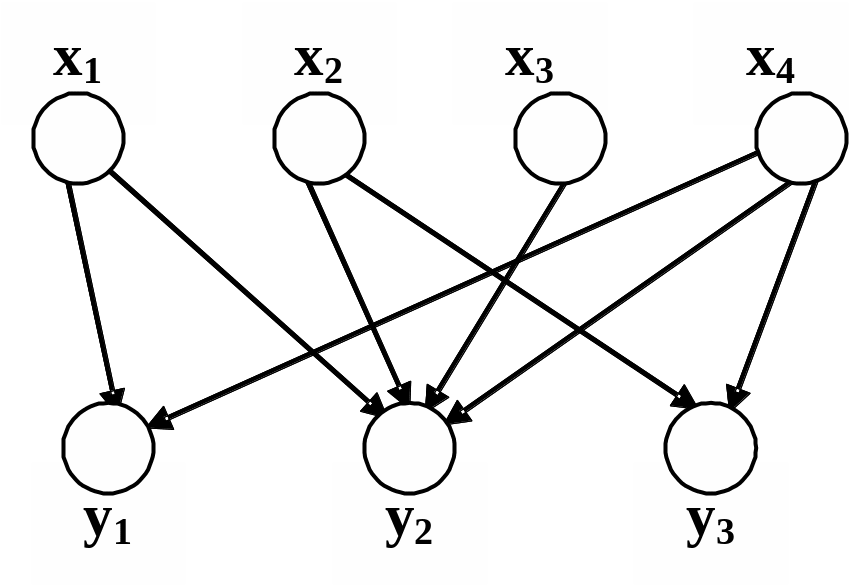
qp={(x1,x2,x3,x4), (y1,y2,y3), (x1,y1), (x1,y2), (x2,y2), (x2,y3), (x3,y2), (x4,y1), (x4,y2), (x4,y3)}.
Рис. 1.11
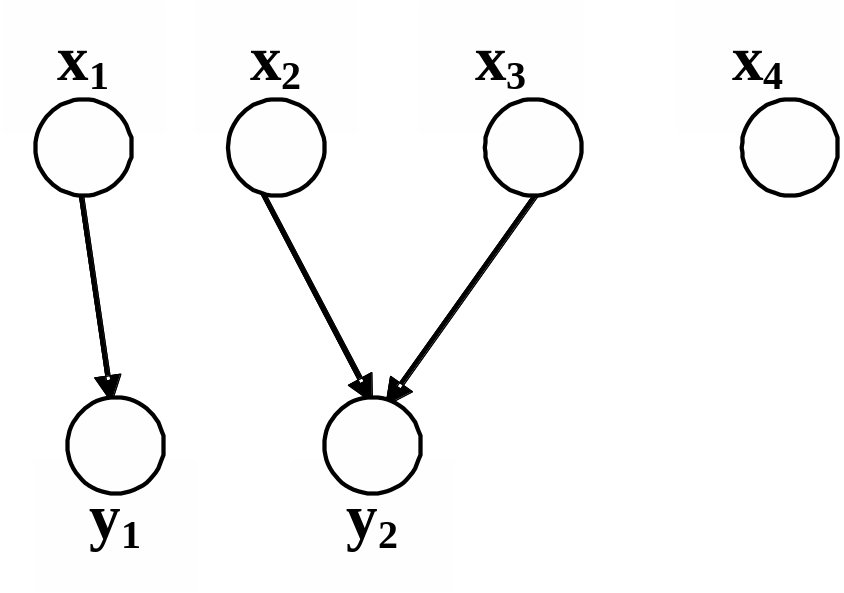
qp={(x1,x2,x3,x4), (y1, y2), (x1, y1), (x2, y2), (x3, y2)}.
Рис. 1.12