3.5. Композиция нечетких отношений
В
теории нечетких множеств рассматривают
композицию нечетких отношений (см.
разд. 2.7.8), которая для двухмерного
нечеткого отношения определена в виде
,
где
- заданное
двухмерное нечеткое отношение на
множестве A1A2
с функцией принадлежности R(x1,x2);
- заданное
одномерное нечеткое отношение на
множестве A1
с функцией принадлежности R(x1);
- заданное
одномерное нечеткое отношение на
множестве A2
с функцией принадлежности R(x2).
Для определения композиции нечетких отношений используют операции проектирования (proj) и цилиндрического расширения (cext).
Операция проектирования нечеткого отношения с , причем А=A1A2,
на одномерное нечеткое множество определяется в виде
.
Пример выполнения операции proj показан на рис. 3.6.
Рис. 3.6
Операция цилиндрического расширения по Заде определяется в виде
=cext(А;
A1A2)
.
Пример выполнения операции cext показан на рис. 3.7.
Операция
композиции нечетких отношений,
определенная в виде
,
с учетом операций проектирования и
цилиндрического расширения определяется
в виде:
,
где операция
задается в виде Т–нормы.
Приведем наиболее часто употребляемые определения операции композиции нечетких отношений.
Рис. 3.7
Если
в качестве Т-нормы
в операции композиции применяется
логическое произведение по Заде (3.6), то
нечеткая композиция называется
максиминной композицией двух отношений
и
.
Функция принадлежности В(x2)
нечеткого множества
будет равна
. (3.32)
Если рассматривать два нечетких отношений и , заданных на U×U, то максиминная композиция этих нечетких отношений будет иметь функцию принадлежности вида
.
Минимаксная композиция двух нечетких отношений и , заданных на U×U, будет иметь функцию принадлежности вида
.
Макси-мультипликативная композиция двух нечетких отношений и , заданных на U×U, будет иметь функцию принадлежности вида
.
Рассмотрим пример, в котором для композиции нечетких отношений функция принадлежности определяется согласно уравнению (3.32).
Пусть
задана нечеткая переменная «5»
с одномерной функцией принадлежности
и
нечеткая переменная в виде нечеткого
отношения «»
с двухмерной функцией принадлежности
пирамидального вида
.
Найдем нечеткую переменную «приблизительно
5 приблизительно равное х2»,
где х2
– заданное число. Согласно уравнению
(3.32) получим:
.
На рис. 3.8 приведена иллюстрация вычисления степени принадлежности В(x2).
Рис. 3.8
а
– композиция нечеткого отношения
;
б
- цилиндрическое расширение 5(x2);
в
- пересечение нечеткого отношения и
цилиндрического расширения; г
- проекция нечеткого множества
.
В рассмотренном примере элементы x1 и x2 заданы на непрерывных областях. Возможен случай задания элементов x1 и x2 на дискретных областях с x1,x2{0,1,2,3,…}. Рассмотрим, как применяется композиционное правило для получения нечеткого вывода на отрезке [0,1]. Получим следующие преобразования:
.
Иллюстрация данных преобразования показана на рис. 3.9.
Рис. 3.9
В виде примера рассмотрим, каким образом можно получить вывод о принятии решения в задаче управления уровнем воды в бассейне. На рис. 3.10 приведена иллюстрация к решению задачи. Вода поступает через вентиль, а уровень воды в бассейне контролируется датчиком. Нечеткая система управления подает на вентиль сигналы управления, определяющие количество поступающей в бассейн воды. Определим лингвистические правила для управления уровнем воды в бассейне.
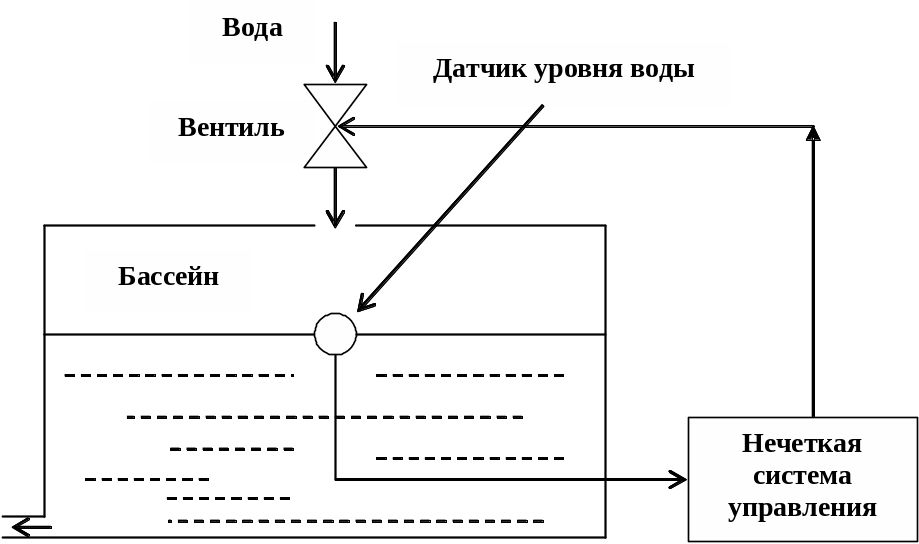
Рис. 3.10
Правило R1: если уровень воды в бассейне низкий (нечеткое множество ), то вентиль открыт (нечеткое множество );
Правило R2: если уровень воды в бассейне не очень высокий (нечеткое множество ), то вентиль слегка открыт (нечеткое множество );
Нечеткий локальный вывод для получения нечеткого множества определяется нечеткой композицией и нечеткой импликацией так, что:
.
При
определении импликации Т-типа
по Мамдани получим для
:
.
Для
нечеткого множества
,
при определении копмозиции по Заде,
получим:
.
Процесс определения В(х) иллюстрирован на рис. 3.11.