Ri: если препятствие впереди, то двигайся влево,
или
Ri+1: если препятствие впереди, то двигайся вправо,
или
……………………………………
База правил противоречива.
Пример непротиворечивой базы нечетких правил следующий:
R1:
если x1=
или x2=
,
тогда y=
;
R2:
если x1=
или x2=
,
тогда y=
;
R3:
если x1=
или x2=
,
тогда y=
.
Если правила содержат два условия и один вывод, то эти правила представляют собой систему с двумя входами x1 и x2 и одним выходом y. Данная система может быть представлена в матричной форме:
x2 |
x1 |
||
|
|
|
|
|
|
y= |
|
|
y= |
|
|
|
|
y= |
|
База нечетких правил непротиворечива.
Для противоречивой базы нечетких правил матричная форма имеет вид:
x2 |
X1 |
||
|
|
|
|
|
|
|
I |
|
|
|
, |
|
, |
|
|
Противоречивая база нечетких правил приводит к неоднозначности выводов при x1= , x2= и x1= или x2= .
Полнота базы нечетких правил связана с полнотой знаний, которые содержатся в базе правил. Если база нечетких правил неполная, то в ней для определенных ситуаций отсутствуют связи между входами и выходами. Но может быть, что результат вывода из правил обусловлен свойствами нечетких множеств, а не из-за неполноты базы правил. Мерой полноты базы нечетких правил является критерий:
,
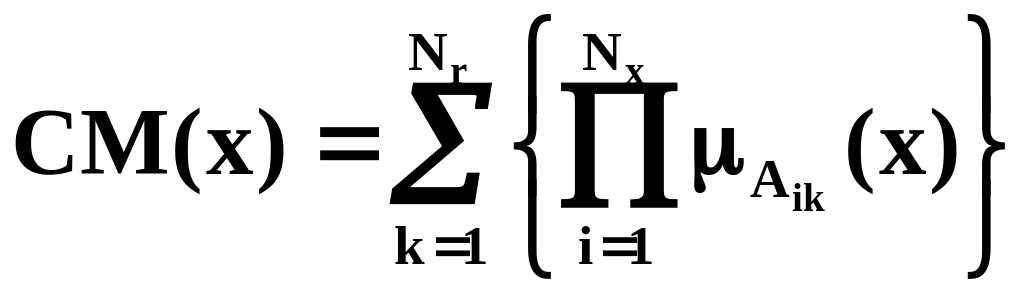где x – физическая переменная входных данных (условий); Nx - число условий в правиле; Nr - число правил в базе правил.
Существует классификация баз нечетких правил по полноте знаний:
- CM(x)=0 – неполная база правил;
- 0<CM(x)<1 – база правил незначительно полная;
- CM(x)=1 – база правил точно полная;
- CM(x)>1 – база правил сверхполная (избыточная).
При разработке алгоритмов и программного приложения для нечетких систем управления следует вначале осуществить проверку базы нечетких правил на непрерывность, непротиворечивость и полноту, а затем приступать к разработке программных модулей.
3.4.2. Нечеткая
импликация.
Продукционное правило (3.31) для одного
вывода может быть представлено в виде
,
где символ «» - нечеткая
импликация;
- функции
принадлежности нечетких множеств
,
соотвественно;
- функция
принадлежности нечеткого множества
(вывода)
.
Нечеткая
импликация является обобщением четкой
импликации и имеет эквивалентные
обозначения:
.
В лингвистических определениях примером четкой импликации является силлогизм, который может быть представлен в виде трех формул.
Формула 1. Заданы четкие переменные: u1 - электрическая печь; u2 – нагрев помещения; u3 – в помещении тепло. Построим следующую схему, приведенную в табл. 3.1.
Переменные |
Формальный уровень |
Лингвистический уровень |
u1, u2 |
y1=u1u2 |
«если электрическая печь, то нагрев в помещении» |
u2, u3 – |
y2=u2u3 |
«если нагрев в помещении, то в помещении тепло» |
Вывод |
y3=u1u3 |
«если электрическая печь, то в помещении тепло» |
Из утверждений: y1=u1u2 и y2=u2u3 следует новое y3=u1u3.
Формула 2. Из утверждения y1=u1u2 («если электрическая печь, то нагрев в помещении») делается вывод y2: «если это устройство печь, то оно греет». Формула 2 известна под названием: правило modus ponens.
Формула
3.
Из утверждения y1:
«если электрическая печь, то нагрев в
помещении» делается вывод
:
«если это устройство не греет, то оно
не электрическая печь».
Подобные формулы существуют и для нечеткой импликации [12].
В нечеткой логике существуют следующие способы вычисления нечеткой импликации.
Нечеткая
импликация S–типа
является аналогом четкой импликации.
Для нечетких формул
и
нечеткая импликация определяется
(Клине, 1938):
.
Степень принадлежности нечеткой
импликации для данного случая определится
по формуле
.
Нечеткая
импликация QL–типа
(QL
– Quantum
Logic)
для нечетких формул
и
определяется (по Рейшенбаху):
.
Степень принадлежности нечеткой
импликации для данного случая определится
по формуле:
.
Модификацией
QL-типа
является импликация «расширение
импликации исчисления высказываний по
Ли»:
.
Степень принадлежности нечеткой
импликации для данного случая определится
по формуле:
.
Нечеткая импликация R–типа (R - аббревиатура «residuated» - «разность, остаток») отражает частичный порядок в предложениях:
.
Нечеткая
импликация T–типа
основана на T
–норме:
.
Примером импликации Т-типа
является импликация по Мамдани (1974):
,
степень принадлежности которой
определится по формуле:
.
Нечеткая импликация, отражающая частичный порядок и основанная на классическом пересечении множеств:
.