3. Нечеткая логика
3.1. Нечеткая операция «и»
Задание нечетких множеств позволяет обобщить четкие логические операции в их нечеткие аналоги. Нечетким расширением операции «И» является триангулярная норма Т, Другим название T–нормы яляется S–конорма. На рис. 3.1 приведено схемотехническое предствление T–нормы.
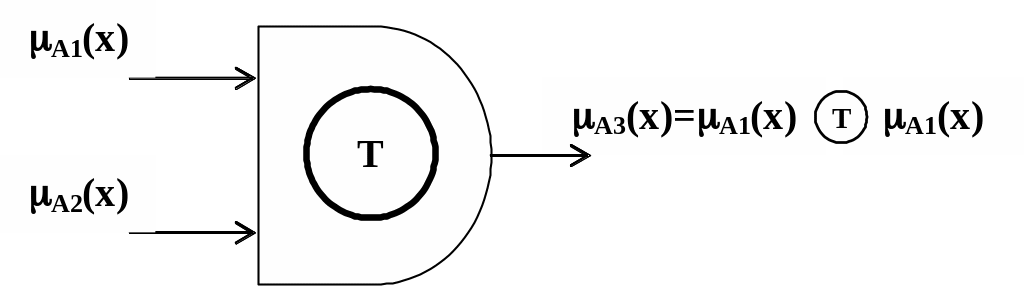
Рис. 3.1
Нечеткая операция «И» в общей форме определяется как отображение:
;
;
;
,
для которых выполняются аксиомы:
- аксиомы граничных условий T–нормы:
;
;
(3.1)
;
;
(3.2)
- аксиомы объединения (перечечения):
;
(3.3)
;
(3.4)
- аксиома упорядоченности:
. (3.5)
В теории нечетких множеств существует бесчисленное количество нечетких операций «И», которые определяются способами задания операции (Т) при выполнении условий (3.1) - (3.2). В теории нечеткого управления применимы следующие способы задания операции (Т), перечисленные ниже.
Логическое произведение [Заде, 1973 г.]:
.
,
xR. (3.6)
Алгебраическое произведение [Бандлер, Кохоут, 1980 г.]:
,
xR, (3.7)
где «.» - произведение, принятое в классической алгебре.
Граничное произведение [Лукашевич, Гилес, 1976 г.]:
, (3.8)
где - символ граничного произведения.
Сильное, или драстическое (drastic), произведение [Вебер, 1983 г.]:
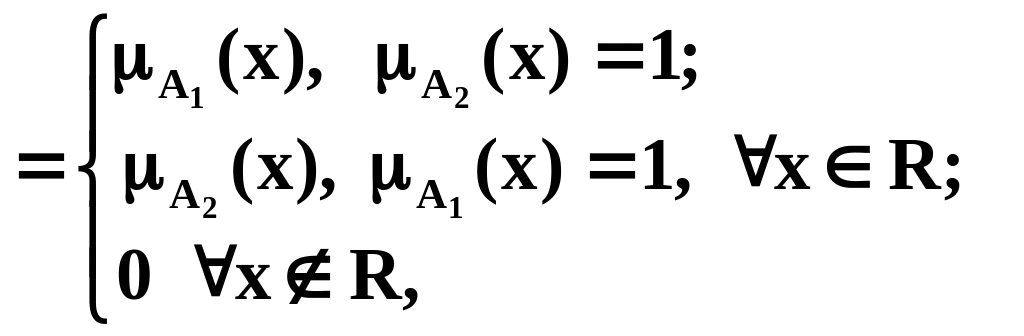(3.9)
где - символ сильного произведения.
На рис. 3.2 показана функция принадлежности при логическом, алгебраическом, граничном и сильном произведении нечетких множеств.
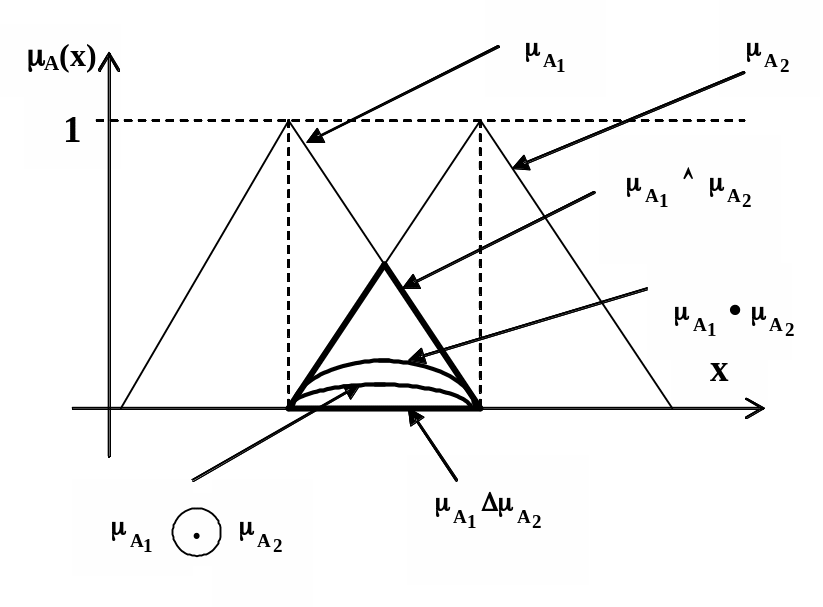
Рис. 3.2
3.2. Нечеткая операция «или»
Нечетким расширением операции «ИЛИ» является S–норма. Иногда применяют название T–конорма. На рис. 3.3 приведено схемотехническое предствление S–нормы.
Нечеткая операция «ИЛИ» определяется как отображение
,
для которого выполняются отображения:
- аксиомы граничных условий T–нормы:
,
; (3.10)
,
; (3.11)
- аксиомы объединения (перечечения):
; (3.12)
; (3.13)
- аксиома упорядоченности:
; (3.14)
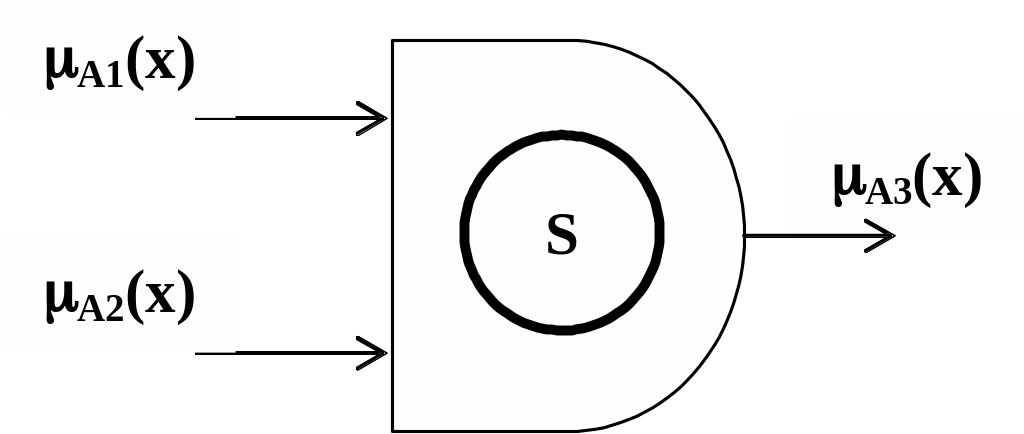
Рис. 3.3
Из бесконечного числа нечетких операций, удовлетворяющих аксиомам (3.10) – (3.14), в теории управления нашли применением следующие операции, перечисленные ниже.
Логическая сумма [Заде, 1973 г.]:
.
,
xR. (3.15)
Алгебраическая сумма [Бандлер и Кохоут, 1980 г.]:
,
xR, (3.16)
Граничная сумма [Лукашевич, Гилес, 1976 г.]:
, (3.17)
Сильная, или драстическое (drastic), сумма [Вебер, 1983 г.]:
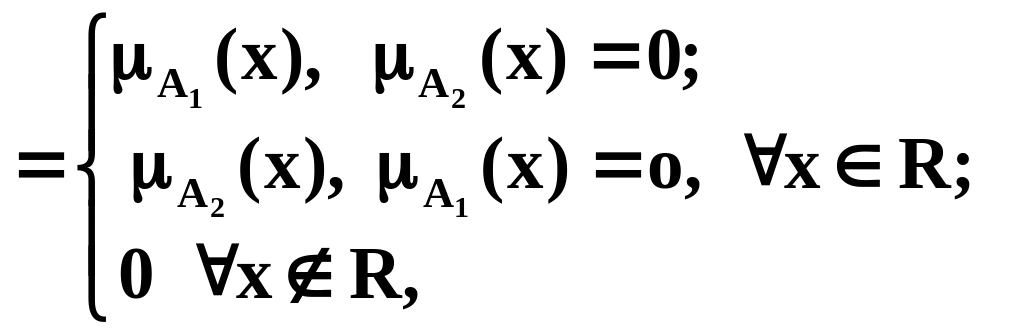(3.18)
Сравнение аксиом T–нормы с аксиомами S–нормы показывает, что различие в них состоит только в аксиомах граничных условий.
На рис. 3.4 показана функция принадлежности при логической, алгебраической, граничной и сильной сумме нечетких множеств.
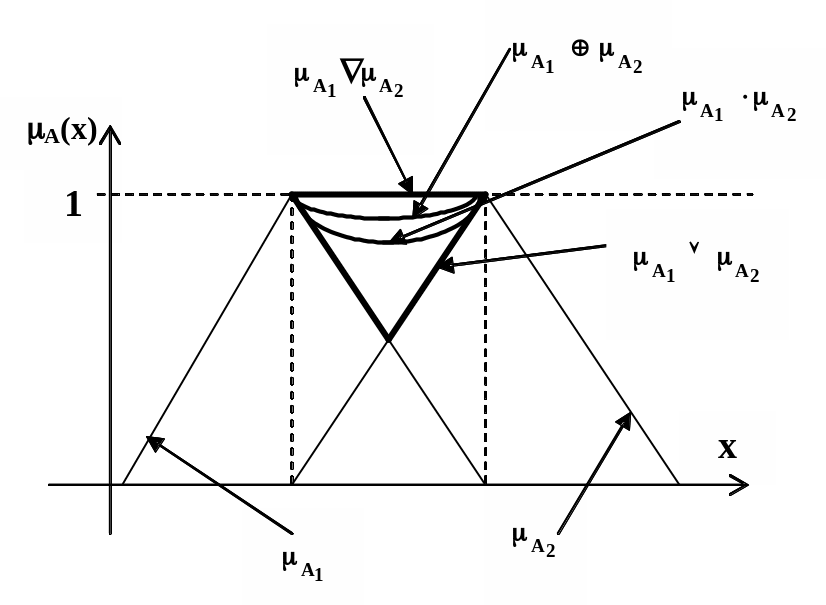
Рис. 3.4
3.3 Нечеткая операция «не»
Операция
нечеткого «НЕ» определяется как
отображение
,
для которого выполняются аксиомы:
; (3.19)
; (3.20)
; (3.21)
Множество отображений, удовлетворяющих аксиомам (3.19) – (3.21), являются нечетким отрицанием. Операция нечеткого отрицания в виде схемы показана на рис. 3.5.
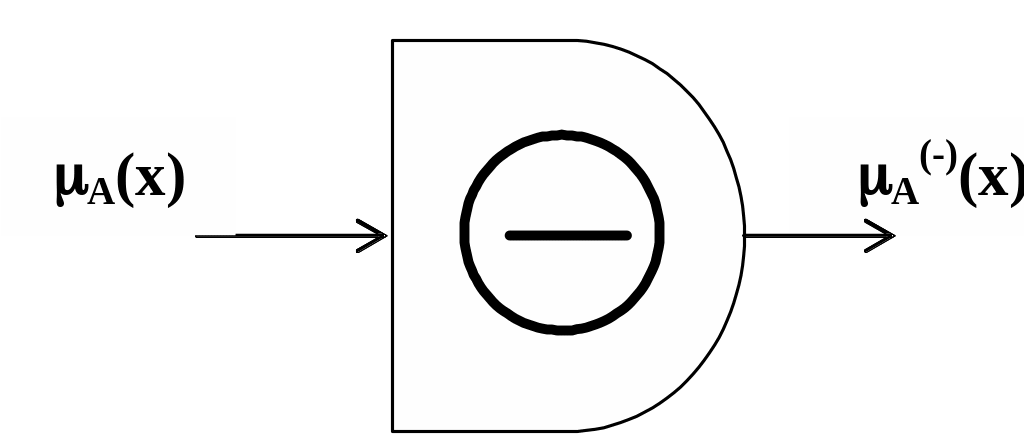
Рис. 3.5
Из бесконечного числа нечетких операций «НЕ», удовлетворяющих аксиомам (3.19) – (3.21), в теории управления нашли применение следующие операции, перечисленные ниже.
Нечеткое «НЕ» по Заде (1973) определяется как вычитание из единицы:
. (3.22)
Нечеткое «НЕ» по Сугено (1977) или -дополнение определяется в виде формулы
. (3.23)
При =0 уравнение (3.23) совпадает с уравнением (3.22).
Нечеткое «НЕ» по Ягеру (1980) определяется в виде формулы:
, (3.24)
где p>0 – параметр. При p=1 уравнение (3.24) совпадает с уравнением (3.22).
Для Т-норм и S-норм могут существовать различные варианты отрицаний из-за бесконечного числа возможных нечетких операций «НЕ». Однако, желательно выбирать такие варианты отрицаний, которые удовлетворяют условиям:
; (3.25)
. (3.26)
Эти условия по аналогии с четкой логикой называют нечеткими законами де Моргана. Операции (3.25) и (3.26) называют взаимно дуальными, т.к. в теории нечетких множеств доказывается, что из (3.25) следует (3.26) и, наоборот, из (3.26) следует (3.25).
Взаимно дуальными являются также следующие нечеткие операции:
; (3.27)
; (3.28)
; (3.29)
. (3.30)