2.8. Нечеткие отношения

2.8.1. Задание нечетких отношений. Нечетким отношением на произвольном непустом множестве X называется и через обозначается пара множеств, в которой является нечетким подмножеством множества X²=XX. Множество X называется областью задания отношения , а нечеткое множество называется нечетким графиком отношения.

Нечеткое отношение есть нечеткое соответствие , у которого X=Y. Носителем нечеткого отношения называется четкое отношение =(X,F), у которого график F является носителем графика . Имеются четыре способа задания нечетких отношений: теоретико-множественный, матричный, графический и с помощью нечетких предикатов (предикатный).

При теоретико-множественном способе перечисляются последовательно множество X={x_i}, и нечеткое множество ={_F<x_i,x_j>/<x_i,x_j>}, x_i,x_jX².

Матричный способ требует задания матрицы смежностей R_, строки и столбцы которой помечены элементами xX, а на пересечении i-й строки и j-го столбца указывается элемент r_ij=_F<x_i,x_j>, где _F - функция принадлежности элементов x_i, x_jX² нечеткому графику .

Задание нечеткого отношения в виде графа предполагает, что граф имеет множество вершин X, а дугам <x_i,x_j> приписаны соответствующие значения _F<x_i,x_j>.

Нечеткое отношение , граф которого показан на рис. 2.19, имеет X={x₁,x2,...,x₅}, F={<0,5/<x₁,x₅>>, <0,7/<x₁,x₃>>, <0,4/<x₂,x₃>>, <0,8/<x₃,x₃>>, <0,2/<x₄,x₃>>, <0,1/<x₄,x₁>>, <0,6/<x₅,x₄>>, <1/<x₅,x₃>>, <1/<x₅,x₅>>}.

Рассмотрим способ задания нечеткого отношения с помощью нечетких предикатов.

Если _F<a,b>/<a,b> , a,bX, то выражение представляет собой нечеткое логическое высказывание, значение истинности которого равно _F<a,b>. Следовательно, для задания нечеткого отношения на X достаточно задать нечеткую логическую формулу от двух переменных или нечеткий предикат, который определен на множестве X², а значения принимает из интервала [0,1].

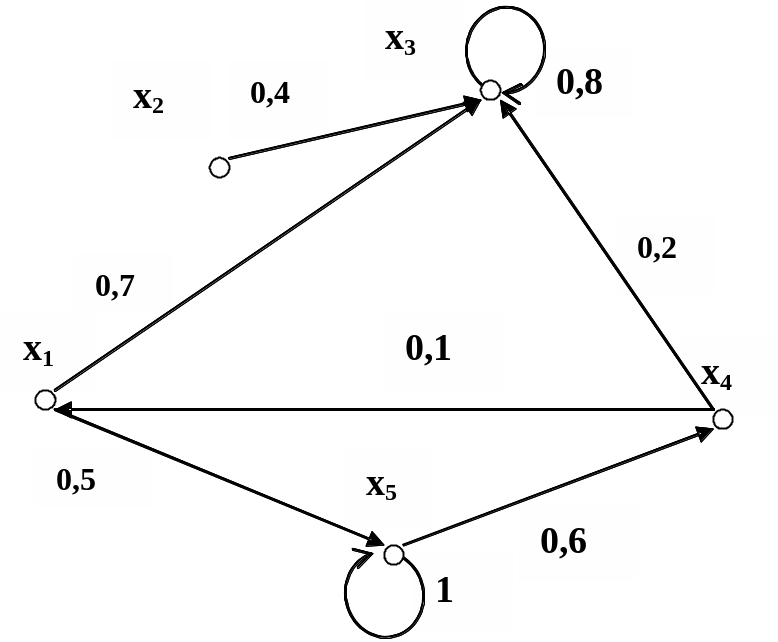
Рис. 2.19

Степень равенства отношений и определится выражением

Отношения и нечетко равны при 0,5, нечетко не равны при 0,5 и взаимно индифферентны при =0,5.

Степенью нечеткости отношения называется величина , где  - носитель нечеткого отношения .

2.8.2. Операции над нечеткими отношениями. Пусть заданы производные отношения и , причем отношение нечетко включается в отношение .

Объединением отношений и называется нечеткое отношение , если . При этом для любых x_i,x_jX выполняется условие _S<x_i,x_j>=_F<x_i,x_j>_P<x_i,x_j>.

Пересечением отношений и называется нечеткое отношение , обозначаемое , если . Для любых x_i,x_jX выполняется условие: _U<x_i,x_j>=_F<x_i,x_j>_P<x_i,x_j>.

Дополнением отношения называется нечеткое отношение , причем для любых x_i,x_jX выполняется условие _F<x_i,x_j>=1-_F<x_i,x_j>/

Инверсией нечеткого отношения называется нечеткое отношение такое, что нечеткий график представляет собой инверсию графика . Для любых x_i,x_jX справедливо <x_j,x_i>=_F<x_i,x_j>

Композицией отношений и называется нечеткое отношение , обозначаемое , такое, что нечеткий график . Для любых x_i,x_jx_kX выполняется условие

Для произвольных , и справедливы следующие нечеткие равенства: ; ; ; ; .

2.8.3. Основные свойства нечетких отношений. Пусть дано произвольное нечеткое отношение .

Степень рефлексивности отношения определится формулой

Отношение нечетко рефлексивно при 0,5, нечетко нерефлексивно при 0,5, и рефлексивно индифферентно при =0,5.

Степенью антирефлексивности называется величина

Отношение нечетко антирефлексивно, если 0,5, нечетко неантирефлексивно при 0,5 и антирефлексивно индифферентно при =0,5. Следует отметить, что если отношение рефлексивно индиффирентно, то это не обязательно антирефлексивно индифферентно и наоборот.

Степенью симметричности отношения называется величина

При величине 0,5 отношение называется нечетко симметрично, при 0,5 называется нечетко несимметрично, а при =0,5 - симметрично индифферентно.

Степень антисимметричности отношения определяется формулой

Отношение называется нечетко антисимметричным при величине 0,5, нечетко антисимметричным при величине 0,5 и антисимметрично индифферентным при величине =0,5.

В общем случае антисимметрично индифферентное отношение не является симметрично индифферентным отношением и наоборот.

Степенью транзитивности отношения называется величина

Нечетко транзитивным называется отношение , если 0,5. Если 0,5, то отношение называется нечетко нетранзитивным, а при величине =0,5 отношение называется транзитивно индифферентным.

Степенью связности отношения называется величина

Нечетко связанным будет называться отношение, для которого величина 0,5. Если 0,5 то отношение будет нечетко несвязанным. При величине =0,5 отношение называется индифферентным относительно связанности.

Описанные выше свойства называют основными свойствами отношений. Регулярные совокупности основных свойств определяют основные типы нечетких отношений.

2.8.4. Отношение нечеткой эквивалентности. Отношение называется нечеткой эквивалентностью, если оно нечетко рефлексивно, нечетко транзитивно и нечетко симметрично.

Степень эквивалентности , определяющая, насколько отношение является отношением нечеткой эквивалентности, определяется формулой

.

При значении степени эквивалентности 0,5 отношение является нечеткой эквивалентностью, при 0,5 отношение не является нечеткой эквивалентностью. В случае, когда =0,5, отношение будет называться индифферентным относительно эквивалентности. В отношении , являющемся нечеткой эквивалентностью на множестве X, элементы x,yX будут называться нечетко эквивалентными, если _F<x,y>0,5.

Примерами нечетких эквивалентностей являются нечеткие отношения «товары примерно одинаковой цены» на множестве товаров, «иметь примерно одинаковые знания» на множестве студентов.

2.8.5. Отношение нечеткой толерантности. Отношение называется отношением нечеткой толерантности, если оно нечетко рефлексивно и нечетко симметрично.

Степень толерантности отношения определяется формулой

.

Отношение будет являться нечеткой толерантностью, если величина 0,5. При значении 0,5 отношение не является нечеткой толерантностью. Если эначение =0,5, отношение является индифферентным относительно толерантности.

Если отношение - нечеткая толерантность на множестве X, то элементы x,yX будут называться нечетко толерантными при условии _F(x,y)0,5.

Отношение нечеткой эквивалентности является частным случаем отношения нечеткой толерантности, т.к. всегда . Выполнение этого неравенства следует из определения степеней эквивалентности и толерантности.

Примерами нечеткой толерантности являются нечеткие отношения «параметры микросхем немного схожи» на заданном множестве микросхем, «цены на разные микросхемы отличаются друг от друга в пределах допустимой разницы» - на множестве, определенном диапазоном цен на микросхемы. Эти отношения нечетко рефлексивны и симметричны, но не транзитивны и являются отношением нечеткой толерантности.

2.8.6. Отношения нечетких порядков. Отношение является отношением нечеткого порядка, если оно нечетко антирефлексивно, нечетко антисимметрично и нечетко транзитивно.

Степень строгого порядка отношения определяется формулой

.

Отношение является нечетким строгим порядком, если величина 0,5. Если величина 0,5, то отношение не является нечетким нестрогим порядком, а при =0,5 отношение называется индифферентным относительно строгого порядка.

Если для отношения нечеткого строгого порядка _F(x,y)0,5, то элементы x,yX связаны отношением нечеткого строгого порядка и элемент x нечетко предшествует элементу y.

Степенью совершенного строгого порядка называют величину

.

При 0,5 отношение является нечетким совершенным строгим порядком.

Отношение называется отношением нечеткого нестрогого порядка, если оно нечетко рефлексивно, нечетко антисимметрично и нечетко транзитивно.

Степень нестрогого порядка определяется формулой

.

Отношение является нечетким нестрогим порядком, если 0,5, если 0,5, то отношение является нечетким нестрогим порядком. При величине =0,5 отношение будет индифферентным относительно нестрогого порядка.

Степень совершенного нестрогого порядка определяется формулой .

Отношение называется нечетким совершенным нестрогим порядком, если величина 0,5.

Примером отношения нечеткого нестрогого порядка является отношение нестрогого включения, определенное на семействе нечетких подмножеств некоторого множества X0.

2.8.7. Отношение нечеткого квазипорядка. Отношение называется отношением нечеткого квазипорядка, если оно нечетко рефлексивно и нечетко транзитивно.

Степень квазипорядка определится формулой

.

При величине 0,5 отношение является нечетким квазипорядком, а при 0,5 не является нечетким квазипорядком. Отношение будет индифферентным относительно квазипорядка при величине =0,5.

Отношения нечеткой эквивалентности и нечеткого нестрогого порядка являются частными случаями отношения нечеткого квазипорядка, поскольку из определения степеней нечеткой эквивалентности, нестрогого порядка и квазипорядка следует, что и .