Федеральное агентство по образованию и науке

филиал государственного образовательного учреждения

высшего профессионального образования

«Московский энергетический институт

(технический университет)»

в г. Волжском

Кафедра «Промышленная теплоэнергетика»

Шамина Г.З.

«Определение показателя адиабаты воздуха»

Методические указания к лабораторной работе

по дисциплине «Термодинамика»

Волжский 2007

1. Цель работы

Экспериментальное определение среднего показателя адиабаты для воздуха в диапазоне комнатных температур.

2. Теоретические основы работы

Адиабатным (адиабатическим) называют термодинамический процесс, происходящий в термодинамической системе без подвода теплоты. Первое начало термодинамики для произвольного термодинамического процесса имеет вид:

[2,с.56] (2.1)

Где - бесконечно малое количество теплоты, подводимое к термодинамической системе;

- бесконечно малое изменение внутренней энергии системы;

- бесконечно малая работа, совершаемая термодинамической системой в результате данного процесса.

Для адиабатного процесса уравнение (2.1) принимает вид:

(2.2)

Для 1 кг. идеального газа справедливы соотношения:

, (2.3)

. (2.4)

Здесь - молярная теплоёмкость при постоянном объёме газа;

- давление;

- бесконечно малое изменение температуры.

- бесконечно малое изменение удельного объёма.

Подставляя (2.3) и (2.4) в (2.2), получим:

(2.5)

Запишем уравнение Менделеева-Клапейрона: pV=RT, где

R – газовая постоянная для заданного идеального газа. ,

- универсальная газовая постоянная; V – удельный объём газа.

Дифференцируя его, найдём связь между , и :

d(pV) = ; (2.6)

Из (2.6) получим:

; (2.7)

Подставляя (2.7) в (2.5), получим дифференциальное уравнение, связывающее объём и давление идеального газа в адиабатном процессе:

. (2.8)

Используя связь теплоёмкости при постоянном давлении - С_Р с теплоёмкостью при постоянном объёме - C_V в уравнении Майера , и вводя обозначение

[2,с.71] (2.9)

получим:

(2.10)

Для идеального газа теплоёмкости С_Р и C_V не зависят от температуры и величина остаётся постоянной.

Проинтегрируем уравнение (2.10), получим:

или (2.11)

Используя свойство логарифмов, получим:

или (2.12)

Уравнение (2.12) называют уравнением адиабаты или уравнением Пуассона, которое определяет упругость идеального газа и зависимость давления газа от различных величин объёмов, занимаемых при любой температуре. Величину «k» называют показателем адиабаты или показателем Пуассона. Численное значение показателя адиабаты лежит для разных газов в пределах 1,33 – 1,67. Оно зависит от числа атомов в молекуле газа и химической структуры их соединения в молекуле.

Для одноатомных идеальных газов – k=1,67. Из реальных газов к ним можно уподобить инертные газы – гелий, аргон, ксенон.

Для двухатомных идеальных газов - k=1,4. Из реальных газов к ним можно уподобить двухатомные газы – азот, кислород, водород и т.д.

Для трёхатомных и многоатомных идеальных газов с линейной структурой молекулы- k=1,4 ( Н₂S , CO₂, H₂O); с нелинейной структурой - k=1,33 (NH₃, CH₄, SO₃).

Согласно молекуллярно-кинетической теории (МКТ) энергетические параметры движения той или иной молекулы газа учитываются числом её возможных степеней свободы ‘i’ из трёх поступательных и трёх вращательных по осям х, у, z в пространстве [ 1 ]. При этом :

; (2.13)

(i – число возможных степеней свободы молекулы идеального газа);

Уподобляя воздух при атмосферном давлении и комнатной температуре идеальному газу, можно сказать что все приведенные формулы справедливы и для воздуха. Кроме того, учитывая что воздух в основе состоит из азота и кислорода, молекулы которых двухатомные, теоретическая величина показателя адиабаты для него составляет: k=1,4.

3. Описание установки и вывод расчётных формул

Состав и функционирование установки (Рис. 3.1):

I – лабораторный модуль (ЛМ) и II – приборный модуль (ПМ).

ЛМ состоит из баллона (1), наполненного воздухом. Баллон соединён с манометром (3). Через клапан (9) «напуск» и через резиновый шланг (6) баллон соединён с компрессором (7) приборного модуля. Клапан (5) предназначен для соединения баллона (1) с атмосферой, а так как его поперечное сечение достаточно велико, то процесс установления атмосферного давления в сосуде происходит достаточно быстро. Изменение давления происходит практически без теплообмена с окружающей средой, поэтому процесс можно считать адиабатным.

С помощью насоса (7) в баллон (1) накачивается воздух, затем закрывают кран (9). Температура в баллоне, при этом, повышается. Через несколько минут температура воздуха в баллоне становится равной температуре окружающего воздуха в лаборатории. Обозначим эту температуру , а давление в баллоне при этом равно:

; (3.1)

Здесь:

- атмосферное давление;

- избыточное давление воздуха, определить которое можно по показанию манометра.

Выберем в сосуде мысленно замкнутую область (2) вдали от клапана. Будем считать, что масса газа (или число молекул) сосредоточенная в этой «области» неизменна, а параметры газа (давление, температура и объём) в этой области изменяются и соответствуют равновесным параметрам газа в баллоне (1), Начальное состояние воздуха в выделенной области баллона характеризуется параметрами , , .

Если клапан (5) открыть на короткое время ( ), часть воздуха выйдет из баллона и давление в нём упадет и станет , выбранная нами «область» увеличится в объёме до значения . Температура воздуха в баллоне понизится, так как при вытекании из него воздух совершает работу против давления окружающего атмосферного воздуха.

Итак, непосредственно когда клапан (5) закрывают, и состояние воздуха в «области» баллона характеризуется параметрами , , . Считая процесс переход воздуха из состояния 1 в состояние 2 адиабатным процессом, из уравнения (2.12) получим:

; (3.2)

После закрытия клапана (5), объём в баллоне не меняется и потому происходит изохорный процесс теплообмена воздуха во времени с окружающей средой. Температура воздуха в баллоне приближается к температуре воздуха в лаборатории , давление по окончании этого процесса становится равным р₃ :

; (3.3)

- избыточное давление в баллоне измеряется по манометру. Параметры воздуха после окончания изохорного процесса , , , причём .

Так как температуры воздуха в первом и третьем состоянии можно считать одинаковыми, а масса газа в выбранной нами «области» постоянной (объём V выбран вдали от клапана), то для состояний 1 и 3 можно применить закон Бойля-Мариотта [3, с.150]:

; (3.4)

Решая систему уравнений (3.2) и (3.4), исключая величины объёмов, получим:

;

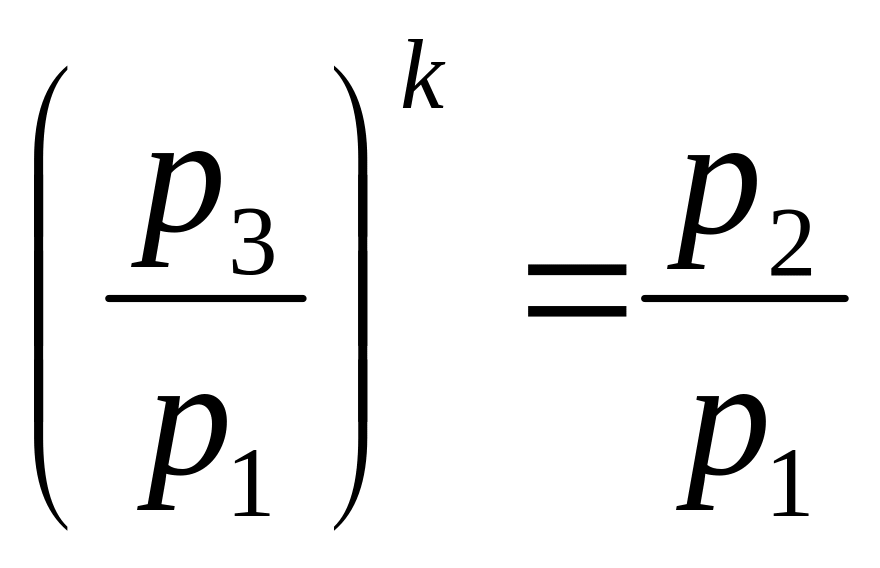Прологарифмировав это соотношение и выразив показатель адиабаты, получим:

;

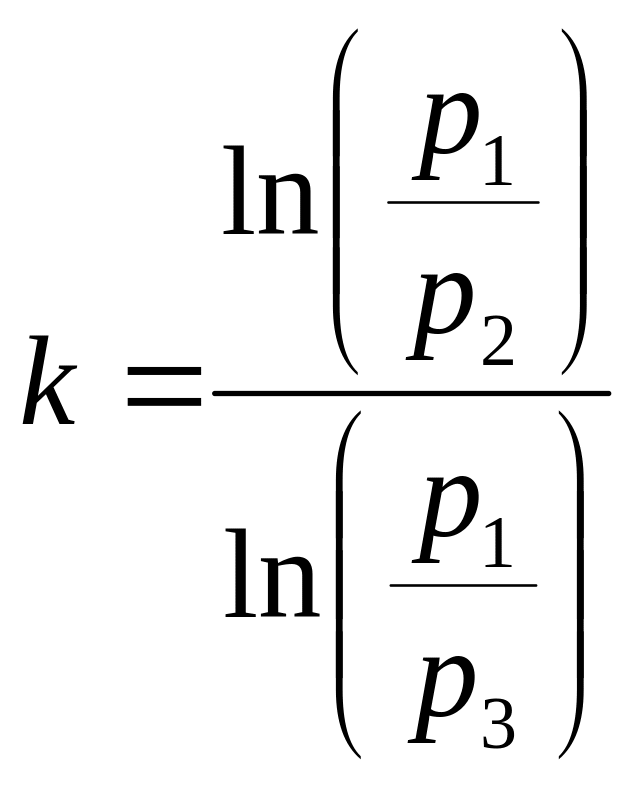Используя соотношения (3.1) и (3.3), получим:

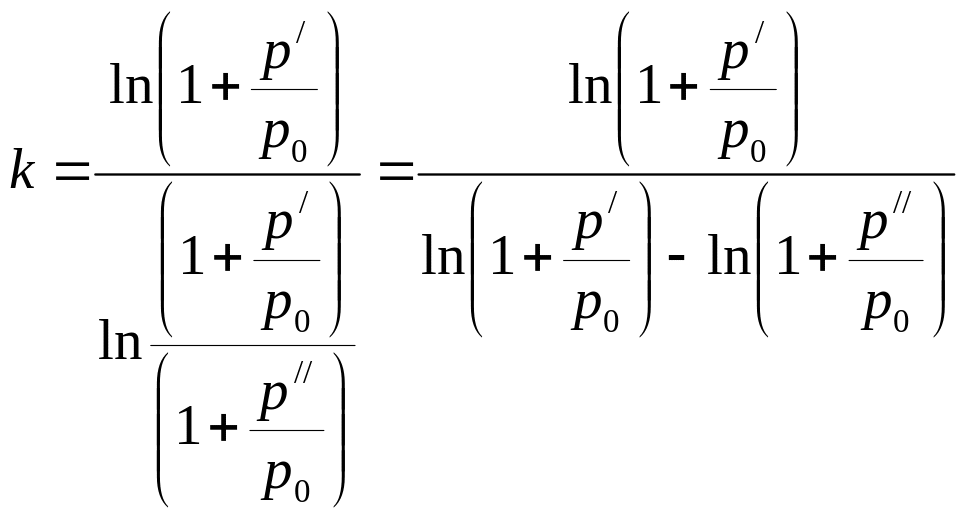; (3.5)

Так как избыточные давления и весьма малы по сравнению с атмосферным давлением , то для данной логарифмической зависимости можно использовать разложение функции типа в сумму числового ряда, ограничившись первым членом разложения (при ):

;

Отсюда из (3.5) следует зависимость показателя адиабаты только от величин избыточных давлений:

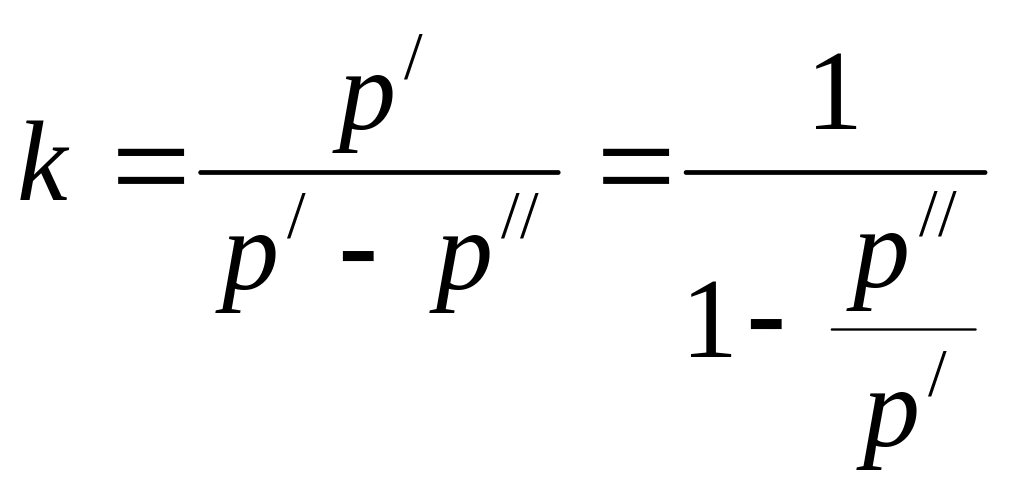; (3.6)

Избыточные давления, определяемые по U-образному манометру, можно выражать соотношением разницы высот уровней жидкости в коленах:

, где (3.7)

- постоянный для данного манометра постоянный коэффициент, зависящий от плотности жидкости - и ускорения свободного падения – g.

Тогда из выражений (3.6) и (3.7) получаем зависимость:

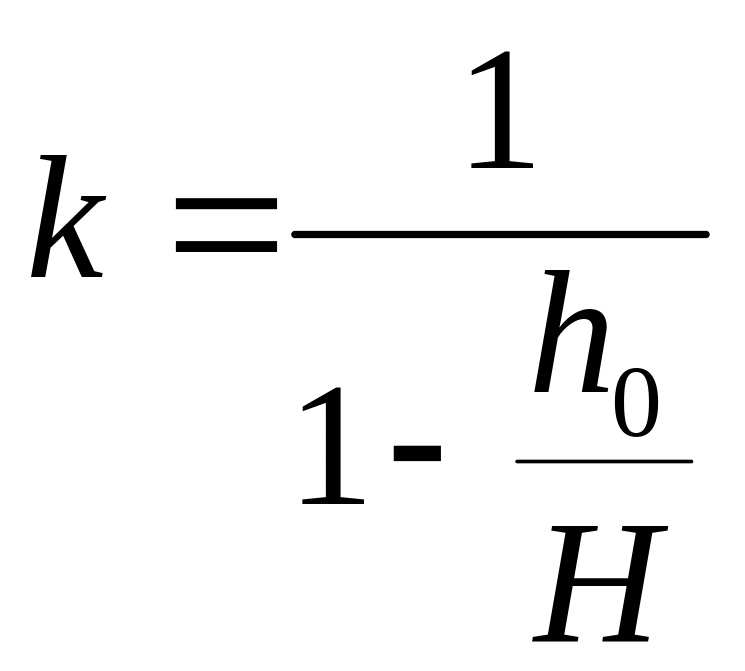; (3.8)

где и - разности уровней жидкости в манометре в первом и третьем состояниях.

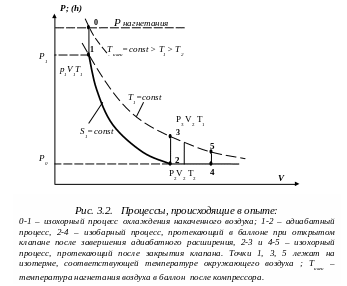
Отметим, что значение соответствует условию, что клапан (5) закрыли точно в момент окончания адиабатного процесса. Если закрыть клапан (5) раньше (до выравнивания давлений), или спустя некоторое время после адиабатного процесса, то результат вычислений по формуле (3.8) даст в первом случае завышенное, во втором – заниженное значение k.. Для получения наиболее точного экспериментального значения k необходимо закрыть клапан точно в момент окончания адиабатного процесса. Т.к. это выполнить вручную во времени технически трудно на данной установке, значение разности уровней определяют косвенным графическим методом.

П р и м е ч а н и е. Процессы, происходящие в сосуде, не являются квазиравновесными, поэтому графики, строго говоря, строить нельзя (в случае неравновесного процесса нельзя говорить о давлении и температуре газа, так как в разных частях баллона эти величины могут иметь различные значения).

Пусть клапан (5) остаётся открытым в течение некоторого времени . В этом случае процессы, происходящие в объёме V, можно условно изобразить графически (Рис. 3.2). Очевидно, что с ростом разность уровней жидкости в манометре будет уменьшаться. При получим , при (длительность адиабатного расширения весьма мала) получим . Измеряя h при различных значениях и строя график логарифмической зависимости изменения давлений ln (h/H) = f( ), можно найти значение экстраполяцией экспериментальной прямой. При постоянных величинах давлений в точке 1 (Н=const) в проводимых экспериментах функцию можно представить в виде ln h = f( ), характер которой представлен на рис. 3.3.