Определение передаточных функций по задающему воздействию и возмущениям.

где - передаточная функция замкнутой системы (иногда ) по задающему (входному) воздействию , - передаточная функция замкнутой системы по внешнему возмущению .

Для одноконтурных систем вида, рис.32

Рис.32

,

Тогда или .

Передаточная функция по ошибке

. (113)

Умножив обе части уравнения на , получим

(114)

- передаточная функция выхода от входа . Передаточная функция замкнутой системы по задающему (входному) воздействию.

Пример 1. Найти передаточные функции от входа и внешних воздействий для системы, рис.33.

Рис.33

;

;

.

Тогда изображение выходного сигнала имеет вид

.

Пример 2. Найти передаточную функцию замкнутой системы, рис.34.

Рис.34

Перенесем узел на выходе за блок с ПФ , рис.35

Рис.35

Тогда передаточная функция первого (внутреннего) контура

,

Передаточная функция второго замкнутого контура (с положит.о.с.)

.

Передаточная функция всей замкнутой системы

.

Метод логарифмических частотных характеристик.

Как отмечалось ранее, частотная характеристика системы представляется следующим образом

- с помощью весовой функции системы

- с помощью преобразования Фурье (как частный случай преобразования Лапласа)

.

Если имеется выражение для передаточной функции, то частотная характеристика получается простой заменой . Так частотная характеристика системы, представленной дифференциальным уравнением -го порядка

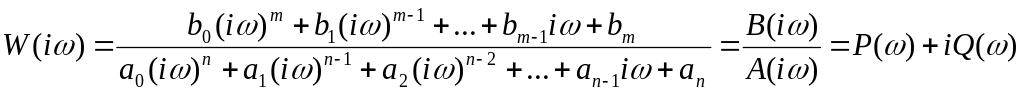. (115)

- вещественная часть частотной характеристики,

- мнимая часть частотной характеристики,

- круговая частота (рад/сек).

Таким образом, частотная характеристика представляет комплексную функцию от частоты .

Представление частотной характеристики(как любого комплексного числа) в полярной системе имеет вид

,

.

Логарифмические амплитудно-фазовые частотные характеристики (ЛАХ) представляют амплитудную и фазовую частотные характеристики, построенные в логарифмическом масштабе.

Логарифмическая амплитудная частотная характеристика – функция

,

построенная в десятичном логарифмическом масштабе частот.

Логарифмической фазовой частотной характеристикой называется фазовая частотная характеристика, построенная в десятичном логарифмическом масштабе частот.

Система координат для построения ЛАХ имеет вид, рис.36

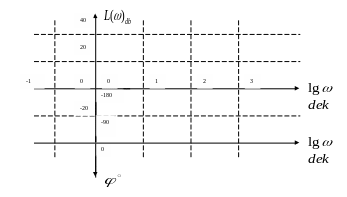
Рис.36

Логарифмические частотные характеристики элементарных звеньев.

частотные характеристики звеньев имеют вид:

, ,

,

, , (116)

.

Соответствующие логарифмические характеристики имеют вид:

1. , рис.37

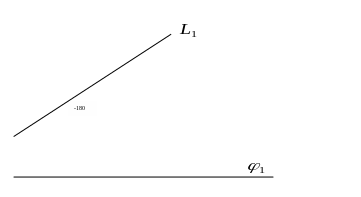
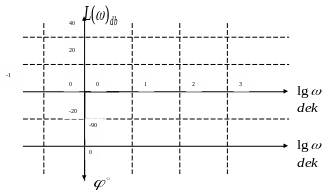
Рис. 37

2. , рис.38.

Для построения амплитудных характеристик удобнее воспользоваться методом построения асимптотических ЛАХ

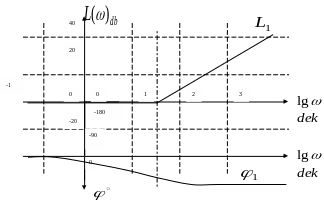
Рис.38