Оператор системы.

Оператором называется закон, в соответствии с которым по заданной (входной) функции определяется другая (выходная) функция.

Понятие оператора является обобщение понятия функции (числу ставится в соответствие другое число). Более общим, чем понятие функция, является понятие функционала.

Функционалом называется оператор, который ставит в соответствие с некоторой функцией число.

Любая динамическая система осуществляет преобразование функций. Поэтому будем говорить об операторе системы

. (25)

Оператор системы может задаваться различными способами. В основном в виде интегро-дифференциальных уравнений.

Линейные и нелинейные системы (операторы). Принцип суперпозиции.

Оператор называется линейным, если он удовлетворяет принципу суперпозиции

. (26)

т.е. если входной сигнал разбить на сумму нескольких сигналов, то применение оператора к сумме сигналов должно равняться сумме результатов применения оператора к каждому отдельному сигналу.

Рассмотрим простейшие примеры (линейного и нелинейного операторов)

1. (27)

тогда .

2. если применить оператор к каждому слагаемому в отдельности, то получим

, т.е. принцип суперпозиции не выполняется.

Линейными являются дифференциальные, интегральные, интегро-дифференциальные оператора, системы линейных уравнений и т.д.

Стационарные и нестационарные системы.

Стационарной называется система, реакция которой на входное возмущение (воздействие) зависит только от интервала времени между текущим моментом и моментом подачи входного возмущения. Таким образом, стационарную систему можно определить как такую систему, у которой при сдвиге во времени входного воздействия без изменения его формы, выходная переменная претерпевает такой же сдвиг во времени без изменения ее формы. Система, которая описывается дифференциальными уравнениями с постоянными коэффициентами, является стационарной.

Непрерывные и дискретные системы.

Входные сигналы в САУ м.б. непрерывными или поступать дискретно (только в определенные моменты времени, разделенные промежутками времени в течении которых они не действуют на систему). Системы первого типа называются непрерывными (или аналоговыми), а второго - дискретными.

Следящий привод – непрерывная система, система телеуправления (сигналы управления поступают дискретно), цифровые системы управления – дискретные (или импульсные).

Характеристики линейных систем. (Реакции на типовые воздействия).

Единичная импульсная функция.

В теории линейных систем удобно использовать в качестве стандартного возмущения единичные мгновенные импульсы. Согласно второму закону Ньютона изменение кол-ва движения равно импульсу действующей на него силы

- импульс силы, или

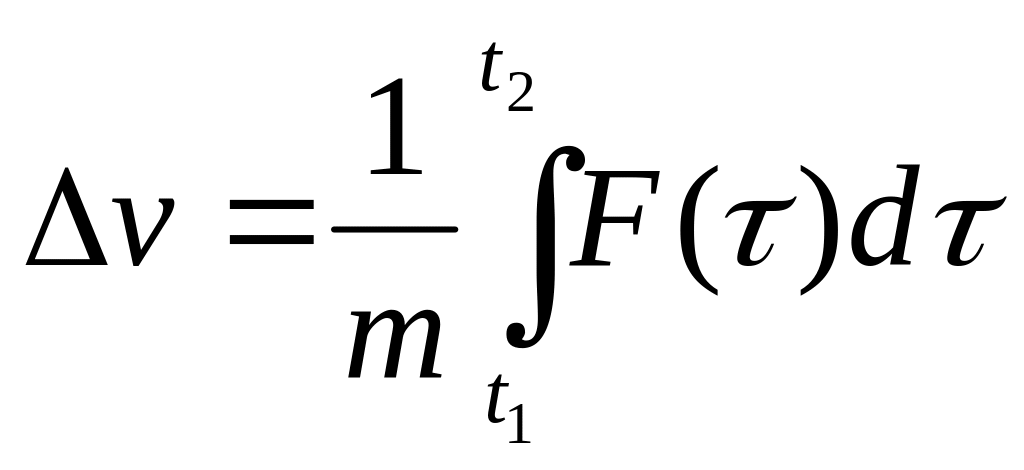, . (28)

Если будем неограниченно уменьшать время действия силы и пропорционально увеличивать силу так, чтобы импульс оставался неизменным, то изменение скорости тела будет оставаться постоянным, например, рис.7.

Рис.7.

В пределе, при нулевой длительности импульса скорость тела (точки) будет мгновенно изменяться на величину импульса, деленного на массу тела. В механике этот случай называется ударом абсолютно твердых тел.

В этом случае функция называется импульсной -функцией Дирака.

Импульсной -функцией называется функция удовлетворяющая следующим условиям:

при ,

при любом (29)

Тогда справедлива следующая важная формула

. (30)

Пределы интегрирования можно произвольно расширить

или

. (31)

Единичная ступенчатая функция.

Удовлетворяет соотношению

, (32)

Действительно

или , откуда (33)

Представление -функции интегралом Фурье.

Любая абсолютно интегрируемая функция (т.е. такая функция, интеграл от абсолютной величины которой в бесконечных пределах имеет конечное значение) может быть представлена интегралом Фурье

, (34)

где

. (35)

Подставим выражения для прямоугольного импульса

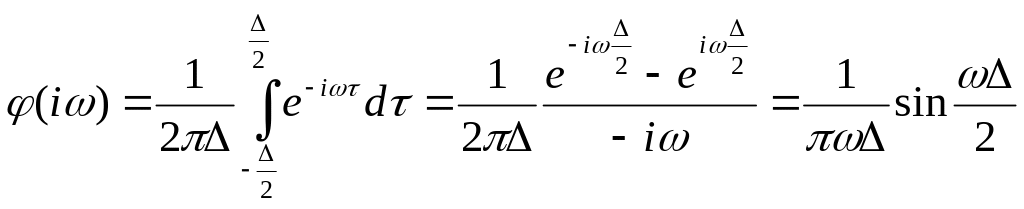. (36)

Подставив в верхний интеграл, получим

. (37)

Переходя к пределу при и учитывая, что при этом , получим

. (38)