Содержание практических занятий

Задание 1. Нахождение ряда фурье и преобразования фурье 2

1.1 Настройка системы МАТЛАБ 2

1.2. Составление программы вывода графиков 3

1.3 Программа вычисления интегралов 4

1.4. Индивидуальное задание 5

Задание 2 Решение задач линейной алгебры 6

2.1. Пример программы работы с матрицами 6

2.2 Индивидуальное задание. 6

Задание 3 Решение краевой задачи проекционным методом Галеркина 7

3.1. Постановка задачи и описание метода 7

3.2. Пример программы: 8

3.3. Индивидуальные задания 9

Задание 4 Нахождение минимума функционала 9

4.1. Пример программы 9

4.2. Индивидуальное задание 10

Задание 1. Нахождение ряда фурье и преобразования фурье

1.1 Настройка системы матлаб

Для работы нам удобно настроить систему так, чтобы на экране всегда присутствовало командное окно и окно редактора m-файлов.

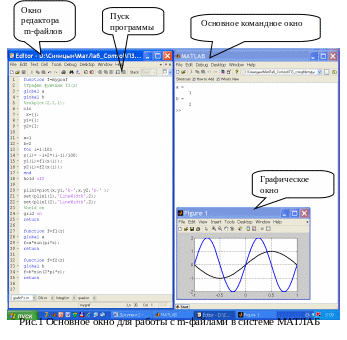
В окне редактора файлов набираются программы вычислений, они записываются каждая под своим именем в созданную папку под именем, например, «студент Петров». После запуска программы ее результаты отображаются в командном окне и в графическом окне.

Для записи m-файла под оригинальным именем используется меню File, Save As. Редактирование файла осуществляется аналогично как в любом текстовом редакторе.

По всем вопросам можно обращаться к меню Help.

1.2. Составление программы вывода графиков

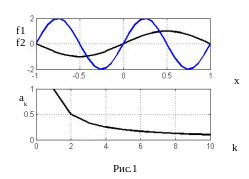
Вначале воспроизведите ниже приведенную программу рисования графика двух функций y1=f1(x), y2=f2(x) и графика функции коэффициентов a_k=a(k), и получите графики вида:

function f=mygraf %основная программа

%График функции f1(x) f2(x) a(k)

global a

global b

Clc %очистка командного окна

x=[]; %очистка массивов (индексы начинаются с 1)

y1=[];

y2=[];

ak=[];

kk=[];

a=1 %задание параметров передаваемых в программу вычисления функций

b=2 %если нет «;» то значение параметра выводится в командное окно

m=30

for i=1:m+1

x(i)= -1+2*(i-1)/m; % вычисление таблиц графиков функций f1(x) f2(x)

y1(i)=f1(x(i));

y2(i)=f2(x(i));

end

for k=1:10 % вычисление таблиц графиков ak(k)

kk(k)=k-1;

ak(k)=1/k;

end

hold off

subplot(2,1,1);

plin1=plot(x,y1,'k-',x,y2,'b-' ); %обращение к программе вывода

set(plin1(1),'LineWidth',2); %установка толщины линий

set(plin1(2),'LineWidth',2);

%hold on

grid on

subplot(2,1,2);

plin2=plot(kk,ak,'k-'); %обращение к программе вывода

set(plin2(1),'LineWidth',2); %установка толщины линий

grid on

return

function f=f1(z) %подпрограмма с глобальным параметром а

global a %эти подпрограммы могут быть записаны в отдельных файлах

f=a*sin(pi*z);

return

function f=f2(z) %подпрограмма вычисления второй функции

global b

f=b*sin(2*pi*z);

return

1.3 Программа вычисления интегралов

Используя предыдущую и нижеприведенную программу, воспроизведем вычисление значений интеграла 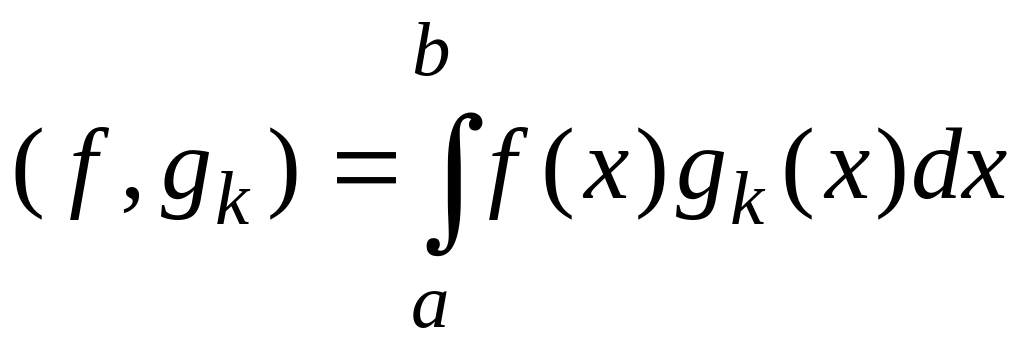, представляющего скалярное произведение заданной функции f(x) на функции выбранного базиса {g_k=sin(kx) , k=1,2,…a= –1, b= +1} для различных значений k, а также график модуля спектральной функции 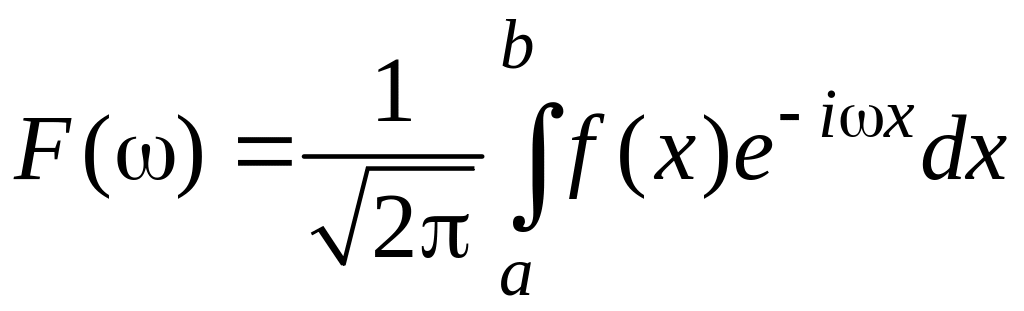видеоимпульса . .

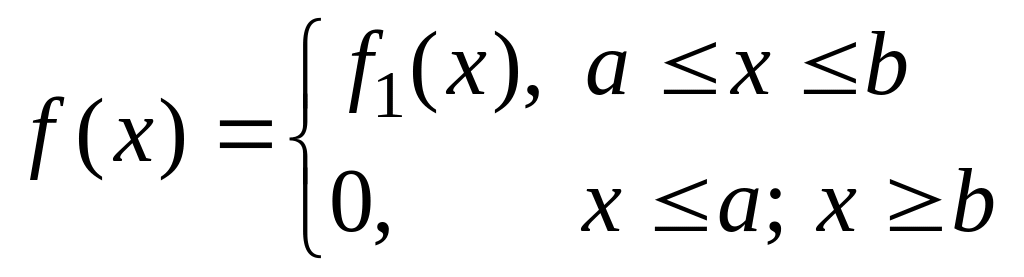function ffff=myintegral_graf

global k

global c

global w

ak=[];

kk=[];

ww=[];

Sw=[];

clc

a=-1

b=1

c=1

% получение графика коэффициентов Фурье периодической функции

for k=1:10

kk(k)=k;

ak(k)=quad(@fg,a,b); % интеграл от a до b функции f(x)*gk(x)

end;

ak

subplot(2,1,1);

plot(kk,ak,'k-');

% получение графика преобразования Фурье видеоимпульса

wh=0.1

for i=1:100;

w=i*wh;

ww(i)=w;

Sw(i)=quad(@fw,a,b); % интеграл от a до b функции fw(x)

end;

qpi=1./2*pi^0.5

subplot(2,1,2);

plot(ww,abs(Sw)*qpi,'b-');

return

function y=fg(x)

y=f(x).*g(x);

return

function y=f(x)

global c

y=x.^3-c*x+1;

return

function y=g(x)

global k

y=sin(k*pi*x);

return

function y=fw(x)

global w

y=f(x).*exp(1i*w*x);

return

Фактически мы получили коэффициенты разложения нечетной функции f(x)=x³-c*x+1 в ряд Фурье по синусам и спектральную функцию непериодического сигнала.