2.7. Физические свойства полярных растворителей

В качестве растворителей в электрохимии, как правило, используются полярные жидкости либо смеси полярных и неполярных жидкостей. Критерием полярностей является способность обеспечивать полную либо частичную диссоци-ацию ионофоров. Согласно модели Борна, это становится возможно в тех случаях, когда ста-тическая диэлектрическая проницаемость сос-тавляет не менее 10–15. Наряду с имеются также другие важные характеристики раствори-телей – плотность, давление насыщенного пара, характеристические температуры ( термические свойства, вязкость, сжимаемость, поверхностное натяжение и термодинамическая устойчивость (часто говорят об «окне» потенциалов устойчивости – интервале, ограниченном потенциалами окисления и восстановления молекул растворителя).

Традиционная химическая классификация растворителей предполагает их разделение на две большие группы – протонные (вода, спирты, простые амиды и т. д., т. е. соединения, содержащие группы –ОН и –NH) и апротонные (табл. 2.8). Наиболее существенное различие двух этих типов растворителей состоит в том, что только в протонных растворителях возможно образование водородных связей между свободными и связанными в сольватные оболочки молекулами. Водородные связи могут образовываться также с анионами электролита или нуклеофильными фрагментами молекул растворенного вещества. Именно водородные связи приводят к ассоциации молекул в протонных средах. В апротонных жидкостях процессы ассоциации (обычно димеризации) являются следствием электростатических ди-поль-дипольных взаимодействий.

Во многих отношениях уникальным, а также наиболее доступным полярным растворителем является вода (табл. 2.9). Малые (в 2-4 раза меньше, чем для других растворителей) размеры молекул воды и, соответственно, малый мольный объем определяют высокую концентрацию в чистой воде (55,5 М) и возможность обеспечения высокой мольной доли растворителя в разба-вленных растворах электролитов. По этой причи-не, а также из-за достаточно высокой диэле-ктрической проницаемости воды менее выраже-нными оказываются отклонения водных раст-воров от идеальности при заданной концен-трации.

Хотя молекула воды может быть эффективно представлена как диполь, дифрактометрические данные однозначно указывают на её квадру-польный характер (рис. 2.5). Симметрия молеку-лы воды ( предполагает наличие квадрупо-льного момента.

Таблица 2.9. Важнейшие свойства воды

Свойство
Молярная масса	18,015	20,027
	0	3,8
	100	101,4
Статическая диэлектрическая про- ницаемость (25 )	78,4	77
Дипольный момент свободной мо- лекулы, Д	1,85	1,94
Время релаксации (25 ), пс	8.32	1,02
Поляризуемость, Кл·	1,62·1	1,20·1
Пекаровский фактор (25 )	0,549

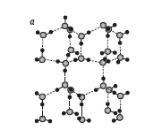
Кластеризация воды представляет собой процесс формирования тетраэдров (рис. 2.6, а) с одной молекулой воды в центре. Представления о тетраэдрической координации были впервые сформулированы Дж. Берналом и Р.Фаулером (1933 г.). К этому заключению достаточно надежно приводят данные дифрактометрии и колебательной спектроскопии. Тетраэдры стаби-лизированы водородными связями и относите-льно слабо коррелируют между собой. Именно такой характер кластеризации определяет наряду с диполь-дипольными взаимодействиями элект-ростатической природы высокую диэлектри-ческую проницаемость воды. При растворении неполярных веществ молекулы воды образуют вокруг них сложные многогранники, стабили-зируемые водородными связями. Типичны, в час-тности, пентагональные додекаэдры (рис. 2.6.б), в объеме которых находится полость размером около 0,5 нм.

Свободные

орбитали

Атом – –2

кислорода ⟺ – ⟺

+ +

+ +

Рис. 2.5. Схематическое представление молекулы воды как эффективного квадруполя

Установлена также возможность кластеризации таких многогранников (рис.2.6,в), которые формируют стабильные кристаллогидраты в жидком состоянии.

Разрушение водородных связей при встраивании воды в сольватные оболочки ионов

б

в

Рис. 2.6. Тетраэдрическая (а)

и додекаэдрическая (б)

структуры воды и схематиче-

ское изображение кластпризо-

ванных многогранников в жид-

жидком кристаллогидрате (в).

(особенно катионов), затрагивающие также вторичные и даже более удаленные от иона гидратные оболочки, обусловливают снижение эффективной диэлектрической проницаемости водных растворов электролитов с ростом их концентрации. Предполагая, что вода в непо-средственном контакте с ионом находится в состоянии диэлектрического насыщения, т. е. практически полностью теряет способность ориентироваться по отношению к внешнему электрическому полю, и имеет при этом ди-электрическую проницаемость около 6, для диэлектрической проницаемости некоторых ра-створов можно получить следующую зависи-мость от концентрации раствора c (в моль/л):

=80 (2.7.1)

где – число молекул воды в окружении иона (число гидратации).

Таким образом, в принципе на основе измерения концентрационных зависимостей диэ-лектрической проницаемости растворов можно проводить определение чисел сольватации ионов. Однако в широком концентрационном интервале линейность -зависимости наруша-ется.

Следует однако иметь в виду, что при образовании ионных пар (в принципе предста-вляющих собой диполи) возможны изменения диэлектрической проницаемости противополо-жного типа по сравнению с описываемыми уравнениями (2.7.1) – увеличение с ростом концентрации. Влияние ионов разной природы на величину снижения диэлектрической проницаемости достаточно специфично и связано с зависящим от химической природы и заряда иона строением сольватных оболочек.

Измерения диэлектрических характеристик воды и других растворителей показывают, что величина снижается с увеличением частоты используемого в эксперименте переменного поля. Частотная зависимость дает информацию о динамическом поведении молекул как в чистом растворителе, так и в растворах. Причиной конечной скорости релаксации является необходимость осуществить переориентацию дипольных частиц, чтобы энергия системы достигла минимума, – этот процесс требует времени от 1 до 100 нс.

Для воды была обнаружена необычная часто-тная зависимость , отвечающая существованию быстрой и медленной подсистем. Формально можно, соответственно, выделить два характер-ных времени релаксации. Обычно полагают, что большее из них (около 8 пс) отвечает релаксации кластеров в целом, а меньшее (около 1пс) – собственно релаксации водородных связей. Не исключено, что динамическая картина на самом деле значительно сложнее и требует усоверше-нствования моделей, применяемых для анализа диэлектрических спектров.

Предельно низкое значение оптической диэ-лектрической проницаемости (оно соответ-ствует только электронной поляризуемости) для воды составляет при 25 1,78 и существенно отличается от измеряемой при частотах ИК-диапазона величины, равной 4,49. Если рассма-тривать быструю и медленную подсистемы как совершенно независимые друг от друга и = 78 считать статической диэлектрической проницае-мостью для медленной подсистемы, то анало-гичная статическая составляющая для быстрой подсистемы оказывается близкой к 6. С учетом этих обстоятельств в сольватационных моделях с пространственной дисперсией диэлектрической проницаемости в качестве характерного значе-ния в структурированных областях (вблизи заряженных частиц и поверхностей) выбирают модельный параметр , равный 5 или 6.

Эмпирические характеристики сольватирую-щей способности растворителей (например, до-норные и акцепторные числа) коррелируют с микроскопическими свойствами, в первую оче-редь с неравномерностью зарядовых распреде-лений в молекулах растворителей, которую можно охарактеризовать величинами электриче-ских моментов разного порядка. Наличие у многоатомных частиц тех или иных составля-ющих дипольного момента , квадрупольного θ и т. д. однозначно определяется симметрией молекул. Величины дипольных моментов традиционно приводятся в литературе во внесистемных единицах – дебаях (Д);

1 Д = 3.336 · 1 Кл · моль. Квадрупольные мо-менты имеют размерность Кл · ; порядок их величин, как правило, 1 Кл ·

Величины дипольных и квадрупольных мо-ментов для многих молекул могут быть рассчитаны с высокой точностью квантово-химическими методами. Однако возможны различия распределений заряда в свободных молекулах в среде; например, при наличии водородных связей в кристаллосольватах поля-рность молекул увеличивается, что может приводить к завышению значений на 50–60%.

Эффективные (усредненные по всем электронным, колебательным и вращательным состояниям молекул) дипольные моменты и одновременно поляризуемости молекул α в отсутствие химических и диполь-дипольных взаимодействий (в том числе водородных связей) можно получить путем измерений диэлектрической проницаемости при разных температурах, применяя уравнение Дебая

= (2.7.2)

(где – мольный объем, k – постоянный Боль-цмана) и проводя соответствующий регрес-сионный анализ. При частотах, превышающих вращательные частоты диполей, в правой части уравнения (2.7.2) преобладает вклад первого слагаемого. Следовательно, подставляя в него вместо можно провести независимое оп-ределение при фиксированных температурах.

Чтобы снизить вклады диполь-дипольных и химических взаимодействий в определяемые ве-личины , измерения диэлектрической проница-емости проводят в разбавленных растворах полярных веществ в неполярных средах (бензол, диоксан, циклогексан). При этом получаются, по-видимому, значения, заниженные примерно на 10% (по сравнению, например, с опреде-ленными для молекул в газовой фазе спектро-скопически). Эти различия можно учесть введе-нием в уравнение Дебая различных поправок (Л.Онзагер, Дж. Кирквуд), учитывающих частот-ную дисперсию диэлектрической проница-емости. Такие поправки одновременно позволя-ют получить и более точные выражения для динамических квазимикроскопических характе-ристик жидкостей – дебаевских времен релак-сации относящихся к более и менее быстрым подсистемам. Однако измерения диэлектриче-ской проницаемости в принципе не позволяет независимо определить составляющие полного дипольного момента.

При рассмотрении явлений сольватации ис-пользуются наряду со статическими диэлектри-ческими проницаемостями также значения так называемого пекаровского фактора (см. табл. 2.8, 2.9) В качестве релаксационной ха-рактеристики применяется иногда динамическая вязкость η, связанная в первом приближении с дебаевским временем релаксации соотноше-нием

(2.7.3)

где – радиус молекулы растворителя.

Используя жидкие растворители при норма-льных условиях, варьировать такие важные хара-ктеристики, как диэлектрическая проницаемость и время релаксации, можно в пределах примерно одного порядка. Поскольку термодинамические свойства растворов электролитов чрезвычайно чувствительны к , а кинетика процессов в раст-ворах – к соответс- твующих величин в рядах растворителей обес-печивает б льшие возможности эксперименталь-ной проверки теории.

Многие растворители (и особенно раствори-тели, склонные к ассоциации) обнаруживают сложное релаксационное поведение в их диэлек-трических спектрах появляется несколько специ-фичных участков в разных частотных диапазо-нах. Эти участки отвечают характерным време-нам различных процессов, сопровождающихся изменением дипольных моментов участвующих в них ассоциатов. Растворители с таким поведе-нием часто называют недебаевскими. Для них соотношение (2.7.3) оказывается неприменимым, а выбор того или иного времени релаксации – зависимым от природы исследуемых динамиче-ских явлений в растворах и на межфазных границах.

Попытки установления границ примени-мости различных физических теорий стимули-руют исследования необычных смешанных

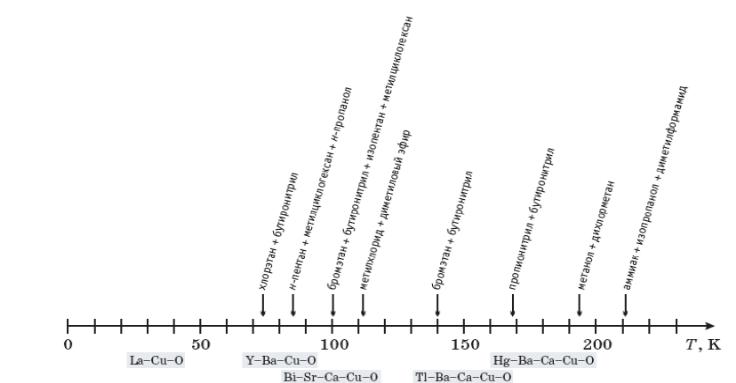
Рис. 2.7. Низкотемпературные квазижидкие системы,

Разработанные в связи с задачами электрохимии купратных сверхпроводников (A = Ba, Sr, Ca; B = La, Y, Bi, Tl, Hg)

растворителей и растворов в различных экстре-мальных условиях.

Можно выделить три уровня конструиро-вания «экстремальных» ион-дипольных систем.

Во-первых, расширить интервал свойств ра-створителей или изменить свойства растворителя при постоянстве его состава можно путем варьирования его температуры и давления в обычной (субкритической) области.

Во-вторых, расширить температурный интер-вал в сторону более низких значений удаётся путем использования специально подобранных смесей растворителей (рис. 2.7), обеспечиваю-щих сохранение квазижидкого состояния вплоть до температур, близких к температуре жидкого азота (77 К). Разработки таких смесей стимули-ровались в 1980-90-е годы развитием высокоте-мпературных оксидных сверхпроводников – в частности, задачей проведения измерений на электродах в сверхпроводящем состоянии в жид-ких растворах. Интервалы температур перехода в сверхпроводящее состояние для нескольких кла-ссов сверхпроводящих купратов разного катион-фного состава показаны на рис. 2.7.

Третьим, быстро развивающимся направле-нием является использование растворителей в сверхкритическом состоянии. Такое состояние (рис. 2.8) достигается при сжатии газа (пара) под давлением выше критического ( при температурах выше критической (T ). Вбли-зи критической точки (кр.т.) происходят резкие изменения плотности и вязкости, а также полярных свойств жидкости. Это связывают с кластеризацией молекул жидкости в агрегаты большого (по сравнению с молекулярным) раз-мера. При переходе в устойчивое сверхкри-тическое состояние (T/ кластеры раз-рушаются, и свойства жидкости снова резко меняются. Некоторые сверхкритические жидкос-ти (скж), находящие практическое применение, перечислены в табл. 2.10.

Аномалии свойств жидкостей в сверхкрити-ческом состоянии определяют целый ряд особых свойств на их основе и возможность интенсифи-кации многих процессов гомогенного и гетероге-нного катализа. Уменьшение полярности упро-щает теоретическое описание жидкостей и раст-воров на их основе. Вода при переходе в сверхкритическое состояние, как и другие жидкости, обнаруживает снижение дипольного момента. При этом почти на три порядка возрастает ионное произведение воды ( при дальнейшем росте T / оно, однако, снижается на несколько порядков по сравнению с обычным для субкритической воды).

Растворимости большинства веществ в свер-хкритических жидкостях достаточно высоки и возрастают с увеличением давления. Темпера-турные зависимости, как и в обычных жидкостях могут демонстрировать как рост, так и снижение предельной концентрации с температурой. Ос-новные тенденции для соотношения раствори-мости полярных и неполярных веществ опреде-ляют снижением полярности растворителя при переходе в сверхкритическое состояние.

Таблица 2.10. Сведения о критических точках некоторых раство-

рителей

Растворитель	Критическая температура,	Критическое давление ×1 Па
Этан	32,3	48,8
Пропан	96,7	42,5
Бутан	152,1	38,0
Гексан	234,1	29,7
Этилен	9,2	50,4
Пропилен	91,9	46,2
Бутен-1	146.5	39,7
транс-Бутен-2	155,5	39,9
Диметиловый эфир	126,9	52,4
Тетрафторметан	–45,6	37,4
Гексафторметан	19,7	29,8
Октафторпропан	71,9	26,8
Гексафторпропилен	94,0	29,0
Дифторметан	78,5	53,4
Трифторметан	26,2	48,6
Хлортрифторметан	28,8	38,7
Хлордифторметан	96,2	49,7
Дифторэтан	113,1	45,2
Тетрафторэтан	101,1	40,6
Пентафторэтан	66,3	36,3
Диоксид углерода	31,0	73,8
Вода	356	220,6