2.4. Реальная и химическая энергии сольватации

Предположим, что металл М погружен в раствор соли этого металла и между электродом и раствором установилось электрохимическое равновесие. Между точкой 1 вблизи металла и точкой 2 вблизи раствора (рис. 2.3) существует измеряемая разность потенциалов 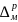ψ – так называемый вольта-потенциал металл/раствор.

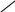
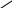
1 Рис. 2.3. Схема для расчета

реальной энергии сольватации

2 иона

χ

3

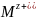
Испарим 1 моль атомов металла, что потребует затраты энергии Ионизируем эти атомы в точке 1 вблизи поверхности металла, затратив на это работу 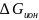. Образовавшиеся в результате ионизации электроны введем обратно в металл. Полученный за счет этого выигрыш энергии составит z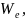 где 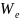– работа выхода электрона из металла. Ионы металла из точки 1 переведем в точку 2. Поскольку между этими точками существует разность потенциалов , то при этом будет затрачена работа 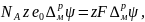где F = – число Фарадея.

Далее ионы металла внесем в раствор. Соот-ветствующий этому процессу энергетический эффект равен так называемой реальной энергии сольватации ионов – 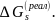Для заверше-ния цикла перенесем ионы из раствора в металл, что в условиях равновесия не требует совершения работы. По закону Гесса,

и, следовательно,

(2.4.1)

Все величины в правой части уравнения (2.4.1) доступны экспериментальному определе-нию, и это открывает путь реальной энергии сольватации отдельного вида ионов. Идея этого метода нахождения была выдвинута А.Н. Фрумкиным. В табл. 2.4 приведены значе-ния для некоторых ионов, рассчитанные по наиболее надежным данным Дж. Рэндлса.

В литературе используется также приведен-ная шкала, в которой за ноль принимаются термодинамические величины для иона водоро-да. Расчеты любых энергий в такой шкале основаны на последовательном рассмотрении сольватации кислот и солей. Например, из свободной энергии (или энтальпии) для HCl определяют парциальные величины для хлорид-иона. Затем используют их в комбинации с данными для NaCl и определяют таким образом парциальные величины для катиона натрия и т.д.

Таблица 2.4. Свободные энергии Гиббса гидратации для некоторых ионов, рассчитанные по уравнению (2.4.1) и (в скобках) полученные в приведенной шкале с использование масс-спектрометрических данных для иона

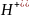
Катион
– кДж/моль	1089 (0)	511 (–575)	411 (–680)	337 (–752)	316 (–775)	284 (–798)

Анион
– кДж/моль	414 (–675)	296 (–800)	271 (–826)	239 (–861)

Выбор в качестве точки отсчета именно иона водорода определяется тем обстоятельством, что для него возможно относительно точное экспе-риментальное определение 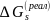методом масс-спектрометрии. Оно основано на измерении сво-бодных энергий и теплот образования кластеров (n от 1 до 6) и последующей экстрапо-ляции к n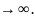 C использованием этой величины приведенная шкала может быть трансформиро-вана в абсолютную. Соответствующие числен-ные значения (в скобках) сопоставлены в табл. 2.4 с результатами расчетов по уравнению (2.4.1) Величина , полученная экстраполяцией масс-спектрометрических данных для (1104 кДж/моль), находится в хорошем согласии с независимым определением работы выхода про-тона из разбавленных растворов (1096 кДж/моль)

На границе воздух/раствор из-за определен-ной ориентации диполей растворителя возникает некоторый скачок потенциала χ – так называ-емый поверхностный потенциал. Поэтому энер-гетический эффект, сопровождающий перенос заряженной частицы через границу воздух/ра-створ (из точки 2 в точку 3 на рис. 2.3), отражает не только ион-дипольное взаимодействие, но и электрическую работу, которая для моля i-х ионов равна 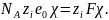Изменение свободной энергии, обусловленное только взаи-модействием ионов с диполями растворителя и отнесенное к молю ионов, называется химиче-ской энергией сольватации . Таким образом, реальная и химическая энергии сольватации связаны соотношением

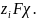= + (2.4.2)

Экспериментально можно определить только ; величины и опытному опреде-лению недоступны. С другой стороны, все моде-льные методы расчета дают , и, следова-тельно, строгая экспериментальная проверка этих моделей невозможна. Поэтому необходимо добиться согласованности результатов в рамках различных модельных расчетов. Один из спосо-бов такого согласования обычно основывается на чисто модельном расчете химической энергии гидратации иона. Другой способ состоит в разложении экспериментальной величины на два слагаемых, причем правило, по которому производится такое разложение, осно-вывается на другом модельном предположении. Так, например, в методе Бернала и Фаулера принимается, что для ионов

=

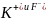
поскольку эти ионы имеют приблизительно оди-наковые радиусы (см. табл. 2.2). Однако величи-ны для одного и того же иона, рассчи-танные разными методами, иногда различаются более чем на 100 кДж/моль. При постоянной и известной в соответствии с уравнением (2.4.2) это отвечает различиям в поверностных потенциалах, превышающим 1 В.

Эти различия значительно превосходят воз-можные ошибки современных модельных оце-нок χ. Такие оценки для водных растворов показывают, что χ = +0,1 В. Это означают, что диполи воды преимущественно ориентированы атомами кислорода в направлении воздушной фазы. Поэтому в настоящее время наиболее точные значения можно рассчитать по уравнению (2.4.2), используя опытные и значения χ, полученные на основе модельных оценок. Для водных растворов при условии, что χ кДж/моль, где 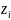учитыва-ет не только величину, но и знак заряда иона. Используя данные Рэндлса, табл. 2.4 и уравнение (2.4.2), можно построить зависимость от обратного кристаллографического радиуса кати-онов и анионов (рис. 2.4). В качественном сог-ласии с моделью Борна, химическая энергия гид-ратации ионов падает с ростом радиуса ионов. Однако при одинаковых размерах катионов и анионов последние гидратируются сильнее. Это может быть объяснено асимметрией диполей воды, благодаря которой положительный конец диполя ближе подходит к центру катиона (К.П.Мищенко). Эффект асимметрии все же не столь значителен, чтобы можно было приравнять химические энергии гидратации и , как это предполагалось в одном из методов разделения величин 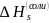на и . Для более стро-гого учета эффекта асимметрии в современных

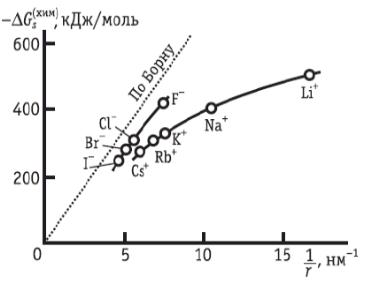
Рис. 2.4. Зависимость химической энергии

гидратации от обратного радиуса иона

моделях молекулы воды рассматривают не как диполи, а как квадруполи. Таким образом, проблема разделения общих термодинамических величин, характеризующих процесс растворения, требует использования нетермодинамических (микроскопических) предположений.