§7 Электромагнитная индукция

1. Явление электромагнитной индукции. Индукционный ток. Правило Ленца. ЭДС индукция. Закон электромагнитной индукции Фарадея.

2. Явление самоиндукции. Индуктивность.

3. Энергия магнитного поля соленоида. Плотность энергии магнитного поля.

4. Взаимная индукция.

5. Электрические колебания.

1. После открытия магнитного действия электрического тока (1820 г.), начался поиск обратного явления – порождение магнитным полем электрического тока. Счастье улыбнулось английскому ученому Майклу Фарадею. В 1831 г. М.Фарадей сделал фундаментальное физическое открытие: он установил, что меняющееся во времени магнитное поле порождает меняющееся электрическое поле – это явление назвали электромагнитной индукцией.

Хорошо известные опыты позволяют установить факты:

1) При любом изменении магнитного потока, пронизывающего катушку, замкнутую на амперметр, амперметр регистрирует ток во время изменения магнитного потока. Поток может изменяться за счёт перемещения вблизи катушки постоянного магнита или другой катушки с током, или за счёт изменения тока в другой неподвижной катушке, или за счёт изменения её формы и размера и т.д. Направление возбуждаемого индукционного тока зависит от знака изменения магнитного потока.

2) Если электромагнитная индукция вызывается изменением какой-либо части установки, то важно лишь относительное перемещение – можно двигать или источник магнитного поля, или измерительную катушку.

3) Эффект выражен тем сильнее, чем быстрее изменяется магнитный поток и чем больше витков имеет измерительная катушка.

4) При заполнении части пространства ферромагнетиком – эффект возрастает. Отсюда следует, что эффект связан с магнитной индукцией В.

5) Если не менять конфигурацию приёмного контура, а менять его сопротивление, то наблюдается эффект: ток уменьшается при увеличении сопротивления и растёт при уменьшении сопротивления. Это позволяет считать, что суть явления заключается в создании электрического поля. Появление тока проводимости является вторичным эффектом.

6) Если присоединить приёмную катушку к электростату (в этом случае замкнутой проводящей цепи не создаётся) и менять магнитный поток через катушку, то наблюдается отклонение указателя электростата. Что свидетельствует о существовании индукционного процесса и в «разомкнутой» цепи.

Совокупность указанных опытов приводит к заключению, что во всех случаях наблюдается возникновение электрического поля. Циркуляция напряженности этого поля взятая по контуру L определяется скоростью изменения магнитного потока Ф пронизывающего этот контур (ЭДС индукции):

.

(7.1)

Это и есть фундаментальный закон электромагнитной индукции Фарадея. Знак «минус» – связан с выбором правой системы координат.

Если ЭДС индукции создаётся в контуре сопротивления R, то в нём возникает электрический ток с мгновенной силой тока

(7.2)

Полный заряд, прошедший по контуру за время изменения магнитного потока

(7.3)

Очень важно, что протёкший заряд не зависит от скорости изменения потока, а определяется только изменением потока.

Направление возникающего индукционного тока определяется правилом Ленца: индукционный ток всегда направлен так, что своим магнитным полем препятствует тому изменению магнитного поля, которое вызвало его.

Если ЭДС индукции вызывается движением магнита, то магнитное поле индукционного тока тормозит движение магнита. Если ЭДС индукции вызывается включением тока в цепи катушки, надетой на общий с контрольной катушкой магнитопровод, то индукционный ток создаёт в магнитопроводе магнитное поле, противодействующее изменению первичного поля и т.д.

Легко понять, что правило Ленца не противоречит закону сохранения энергии для рассматриваемого процесса, но отражает другой закон, закон регулирующий направление процессов, т.е. второе начало термодинамики.

Справедливость правила Ленца можно продемонстрировать рядом эффективных опытов. Если над магнитной стрелкой вращать медный диск, то стрела увлечётся диском и начнёт вращаться в ту же сторону. Между стрелкой и диском помещают лист диэлектрика, чтобы исключить завихрение воздуха. Над медным диском можно вращать магнит, тогда диск придет во вращение. Эта идея используется в конструкции асинхронных двигателей переменного тока.

Рис. Увлечение магнитной стрелки вращающимся диском.

В обоих примерах наводятся вихревые токи или токи Фука. Токи Фука находят применение в различных технических устройствах, например в виброгасителях.

2. Важным проявлением электромагнитной индукции является самоиндукция проводников. Самоиндукция отражает симметрию явления.

Всякий контур, по которому протекает электрический ток, создаёт магнитный поток через поверхность, ограниченную этим контуром. При изменении магнитного потока, связанного с этим контуром, в нём возникает ЭДС, называемая ЭДС самоиндукции. Магнитный поток, создаваемый проводником, зависит от силы протекающего тока и от формы проводника.

Способность проводящего контура создавать магнитный поток, при протекании по нему электрического тока называют индуктивностью.

, .

(7.4)

Ф – полный поток, создаваемый контуром.

Так полный магнитный поток, создаваемый соленоидом длиной ℓ, имеющим N витков будет:

(7.5)

Здесь: – магнитный поток одного витка; число витков на единицу длины.

Сравнив его с (7.4) можно найти индуктивность соленоида.

.

(7.6)

V – объём соленоида.

Таким образом, индуктивность соленоида определяется его геометрическими характеристиками: объемом и плотностью витков (V,n) и характеристиками среды (μ).

Индуктивность в магнитостатики играет ту же роль, что емкость в электростатике. За единицу индуктивности 1 генри принимают индуктивность такого проводника, который при пропускании по нему тока 1 ампер, создает магнитный поток в 1 вебер.

Объединив (7.1) и (7.4) для самоиндукции получаем:

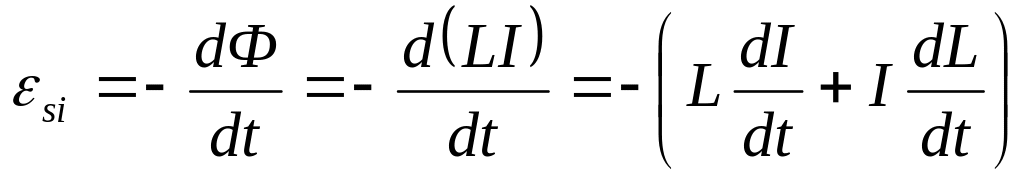
(7.7)

Во многих случаях 2-е слагаемое обращается в 0, что упрощает использование (7.7).

.

(7.8)

3. Энергия магнитного поля. В электростатике вычисляют энергию электрического поля в объеме, где сосредоточены заряды. Энергию поля можно выразить как в терминах создающего его заряд, так и в терминах поля (напряженность и потенциал). Аналогично энергию магнитного поля можно выразить через значение магнитной индукции. Рассмотрим магнитостатическую систему – совокупность электрических проводников, по которым протекают постоянные токи. Они взаимодействуют между собой по средствам магнитного поля, что проявляется в существовании силы Ампера. Такая система токов вполне аналогична статической системе заряда. Роль элементарного магнитного заряда выполняет бесконечно малый элемент тока

(7.9)

Энергия системы токов заключена в энергии их взаимодействия между собой. Энергия взаимодействия возникает как результат совершения работы внешними силами над токами против магнитного поля тока при создании магнитостатической системы. Для создания самого магнитного поля тока никакой дополнительной работы производить не нужно. При перемещении токов под действием сил Ампера, именно магнитное поле совершает работу над током (5.4).

.

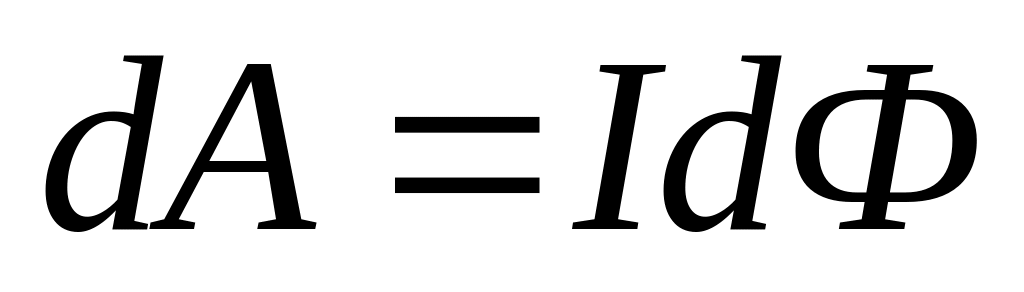Здесь: dФ – изменение магнитного потока при перемещении тока. Используя (7.4) находим:

.

(7.10)

Теперь работу по созданию магнитного поля или энергию этого поля можно найти по формуле:

(7.11)

Её можно выразить через характеристики поля и считаь энергией поля

(7.12)

Это выражение позволят перейти к плотности энергии магнитного поля:

(7.13)

Соотношение (7.13) справедливо всегда.

4. Взаимная индукция. Пусть взаимодействуют два контура. Магнитный поток, сквозь поверхность охваченную контуром 2, может быть создан током I₁ в контуре 1.

Магнитный поток сквозь контур 2 зависит от размера контура 2, его расстояния до контура 1, ориентация относительно этого контура и от силы тока I₁ аналогии с (7.4) можем записать:

(7.14)

L₂₁ – коэффициент пропорциональности, который называют взаимной индукцией контура 1 и 2.

Если контур 2 имеет сложную конфигурацию, например несколько витков, то вместо потока Ф₂ следует пользоваться потокосцеплением Ф₂=NФ₀₂ при изменении тока I₁ в контуре 1 возникает ЭДС самоиндукции. Но в контуре 2 также изменяется магнитный поток Ф₂. Отсюда следует, что возникает ЭДС взаимной индукции.

(7.15)

Здесь использовано (7.13) в предположении L₂₁ – const (см. замечание к (7.7)). Из (7.13) видно, что и взаимная индукция измеряется в генри.

1.Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – 7-е изд., стер. – М: Высш. шк., 2003. – 541 с.: ил.