§3. Энергия электрического поля

Энергия системы зарядов. Энергия заряженного проводника. Энергия заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии.

[1] § 95.

1. Электростатические силы взаимодействия консервативны, следовательно, система электрических зарядов обладает потенциальной энергией. Для ее нахождения пользуются принципом суперпозиции.

.

(3.1)

Здесь – потенциал точки, где расположен заряд . Коэффициент ½ учитывает повтор слагаемых при суммировании.

2. При зарядке тела, приходится преодолевать силы взаимного отталкивания, т.е. необходимо совершить работу численно равную (2.4):

.

(3.2)

И здесь, коэффициент интегрирования ½ учитывает повтор слагаемых¹⁰.

Таким образом, уединенное заряженное тело обладает запасом потенциальной энергии:

(3.3)

3. При зарядке конденсатора происходит перераспределение свободных носителей между обкладками. Заряд q переносится c одной обкладки на другую. Одна обкладка заряжается положительно, а вторая – отрицательно, но в целом конденсатор остается электронейтральным (закон сохранения заряда). При переносе заряда преодолеваются силы электростатического отталкивания, т.е. совершается работа или идет пополнение потенциальной энергии конденсатора. Повторив выкладки (3.2 – 3) с учетом, что для конденсатора говорят о напряжении, получают для энергии конденсатора:

.

(3.4)

4. Энергия системы зарядов, заряженного тела и заряженного конденсатора – это энергия электрического поля. Чтобы выразить энергию поля через характеристики поля можно воспользоваться соотношением (3.4) формулой электроемкости плоского

конденсатора и соотношением (2.5)

(3.5)

Здесь: – объем конденсатора.

Найдем объемную плотность энергии (П/V):

.

(3.6)

Здесь все характеристики относятся к полю. Под нужно понимать плотность энергии поля в бесконечно малом объеме , т.е. плотность энергии задана для некоторой точки.

Источники информации

1.Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – 7-е изд., стер. – М: Высш. шк., 2003. – 541 с.: ил.

Лекция 3

§4. Квазистационарные токи. Постоянный электрический ток

Электрический ток. Сила тока. Плотность тока.

Сопротивление проводников. Закон Ома. Закон соединения проводников. Зависимость сопротивления от температуры. Сверхпроводимость.

Источники тока. Электродвижущая сила (э.д.с.). Закон Ома для полной цепи.

Работа и мощность тока. Закон Ленца-Джоуля.

[1] §§ 96-101

Плазма. [1] § 108.

1. Упорядоченное движение зарядов одного знака относительно зарядов другого знака называют электрическим током.

Электрический ток возникает в системе при выполнении двух условий: наличие свободных зарядов, наличие электрического поля или сторонних сил.

Электрический ток характеризуют «силой тока».

Сила тока показывает, какой заряд протекает через поперечное сечение проводника за единицу времени:

, .

(3.1)

Току приписывают направление – направление движения положительных зарядов.

Распределение тока по поперечному сечению проводника характеризует плотность тока:

, .

(3.2)

На практике использую более мелкую единицу А/мм².

Плотность тока можно выразить через заряды носителей, их концентрацию и скорости упорядоченного движения:

.

(3.3)

2. При перемещении заряда по проводнику электрическое поле (или сторонние силы) совершает работу. Работу по перемещению пробного заряда из одной точки в другую называют падением напряжения или просто напряжением.

.

(3.4)

Между падением напряжения и силой тока существует пропорциональная связь. Коэффициент пропорциональности называют электрическим сопротивлением:

, .

(3.5)

Георг Ом изучал зависимость падения напряжения от силы тока и установил, что существуют проводники, у которых сила тока прямо пропорциональна падению напряжения:

.

(3.6)

Это утверждение называют закон Ома.

Воспользовавшись понятием сопротивление, закон Ома можно сформулировать как независимость сопротивления ни от падения напряжения, ни от силы тока.

Проводники, подчиняющиеся закону Ома, называют омическими. К счастью, существуют не омические проводники, у них нет линейной зависимости между напряжением и силой тока. Их еще зовут нелинейными проводниками.

На схеме сопротивление обозначают знаком показанном на рис. 4.1.

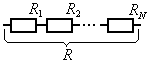
Проводники можно соединить последовательно, параллельно и комбинированно. При последовательном соединении общее сопротивление равно сумме частных:

.

(3.7)

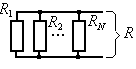
При параллельном соединении складываются обратные величины:

.

(3.8)

Рис.4.1 Обозначение сопротивления на схеме	Рис. 4.4 Последовательное соединение проводников	Рис. 4.3 Параллельное соединение проводников

Зависимость сопротивления от температуры можно представить степенным рядом:

, .

(3.9)

Здесь – сопротивление при ноле Цельсия.

Для не очень больших температурных интервалов ограничиваются первой степенью температуры:

.

(3.10)

В начале ХХ в. Г. Камерлинг-Оннес провел измерения сопротивления вблизи 0 К. Измерения показали, что у металлов и сплавов в диапазоне (0,14 – 20) К, сопротивление скачком падает до нуля. Именно до нуля! Это явление назвали сверхпроводимостью, а температуру перехода в сверхпроводящее состояние – критической точкой.

У каждого проводника своя, характерная для него критическая точка. В 80-х годах ХХ в. были обнаружены вещества, с критической точкой около 100 К. Их назвали высокотемпературные сверхпроводники.

Для омических проводников справедлива формула:

.

(3.11)

Здесь: и – длина и поперечное сечение проводника, коэффициент пропорциональности называют удельным сопротивлением; . Удельное сопротивление величина, характерная для каждого вещества, ее помещают в справочники. Температурная зависимость удельного сопротивления ведет себя также как температурная зависимость сопротивления.

3. Для поддержания электрического тока в цепи необходим участок, где разделяются разноименные заряды, такой участок цепи называют источником тока. Силы, разделяющие разноименные заряды в источнике тока носят неэлектростатическую природу и их называют сторонние силы. Природа сторонних сил различна, так в гальваническом элементе это химические силы, в механических генераторах – сила Лоренца и т.п.

Сторонние силы совершают работу, которая идет на поддержание электрического поля в цепи. Эту работу принято характеризовать «электродвижущей силой». Электродвижущая сила (э.д.с.) – работа по перемещению пробного заряда по замкнутой цепи:

.	(3.12)
Источник тока на схеме изображают значком

С учетом электродвижущее сил для замкнутой цепи справедливо соотношение – закон Ома для полной цепи:

.

(3.13)

Здесь: – сопротивление внешней цепи, – внутренне сопротивление источника тока.

4. Работа электрических сил по перемещению заряда, в конце концов, превращается в теплоту и рассеивается:

.

(3.14)

– количество теплоты, выделяющееся на участке цепи, – падение напряжения на этом участке, – сила тока в цепи, – время.

Впервые это соотношение опытным путем установил в России Э.Х. Ленц и в Англии – Дж. Джоуль, поэтому (3.4) называю законом Ленца – Джоуля.

Закон Ленца – Джоуля отражает закон сохранения энергии и говорит о переходе упорядоченного движения в хаотическое.

Из соотношения (3.14) или (3.4) получают мощность электрического тока:

,

(3.15)

5. Плазмой называю частично тли полностью ионизованный газ. Вещество в состоянии плазмы самое распространенное состояние во Вселенной. Это все звезды. Свободные заряды в проводнике также плазма (низкотемпературная).

Плазма находит широкое применение в различных технологических процессах.

()

Источники информации

1.Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – 7-е изд., стер. – М: Высш. шк., 2003. – 541 с.: ил.

Лекция 4 .