1.6. Упрощённая модель канала передачи.

Для упрощения рассуждений обозначим импульсную характеристику канала , которая создается при распространении сигнала. Принятый сигнал по (2) имеет вид:

. (3)

Формула (3) справедлива в том случае, если ИХ короче защитного интервала, т. е. , тогда символы не перекрываются, а также при стационарности ИХ в течение символа, т.е. в формуле (2) . В формуле (3) - отсчёты аддитивного шума в канале, которые получаются после прохождения белого шума (БШ) через канал. В предположении полной синхронизации приёмника с передатчиком по времени и частоте можно представить выражение в частотной области, т.е. на выходе FFT, получим:

, (4)

где - частотная характеристика канала; - отсчёты спектра шумового воздействия, т.е. .

1.7. Эффекты искажения принимаемых сигналов, вызванные нарушением синхронизации.

Для того чтобы определить, как скажется задержка в канале на его спектр, воспользуемся известным соотношением: если на входе сигнал задержан на , т.е. , тогда его спектр претерпевает изменения . Перепишем соотношение (4) с учётом сдвига по времени согласно [5]:

.

Если представить 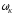через период дискретизации, т.е. , то, введя обозначение , получим

,

где - временной сдвиг, исчисляемый в периодах дискретизации. Таким образом, фаза каждой поднесущей поворачивается на угол, пропорциональный её номеру (индексу) .

В работе [5] показано, что при достаточно больших временных сдвигах помимо фазового искажения также возникает ослабление сигнала на выходе FFT и интерференция, т.е.

,

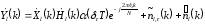где 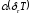- ослабление, а - аддитивный шум, возникающий вследствие интерференции между символами и интерференции между поднесущими [5].

Для определения зависимости спектра сигнала от рассогласования несущих частот сигнала и приёмника , известно соотношение [5]:

,

где - относительная частотная расстройка, - аддитивный шум, возникающий вследствие интерференции между поднесущими.

Если помимо сдвига несущих частот возникает расхождение частоты дискретизации от номинального значения, то сигнал на выходе FFT имеет вид:

,

где ,

а определяется изменением периода дискретизации, при этом новый период дискретизации определяется как [5].

1.8. Алгоритм синхронизации.

Рассмотрим сигнал в виде аддитивной смеси задержанной по времени и смещенной по частоте полезной составляющей и аддитивного белого гауссовского шума:

. (5)

Для синтеза соотношений, определяющих коррекцию по времени и частоте, используем корреляционные свойства передаваемого сигнала во временной области. Ранее упоминалось, что передаваемый символ состоит из информационной части и её циклического продолжения 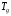- защитного интервала, который передаётся в начале символа.

Обозначим - отсчёт входного сигнала в момент времени , а - отсчёт входного сигнала, который поступил на позже.

Совместная плотность распределения вероятности (ПРВ) случайных центрированных величин и , имеющих нормальное распределение согласно [13] имеет вид

,

где - дисперсия; - мощность сигнала; а - мощность шума. Коэффициент корреляции определяется как

.

В данном случае сигнал комплексный, причём фазы отсчётов различаются, поэтому ПРВ для них примет вид:

, где , а

. (6)

При отсутствии синхронизации по времени выполняется условие , т.е. информационная часть и циклическая не совпадают, поэтому ПРВ можно определить как:

.

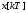Определим функцию правдоподобия (ФП) как отношение совместной ПРВ отсчётов и при наличии корреляции к совместной ПРВ отсчётов и при отсутствии корреляции и усредним её по всей длине .

. (7)

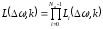, где - ФП для отдельной пары отсчётов и . С учетом условия после преобразований и упрощений получим:

,

где , а .

После логарифмирования обеих частей формулы (7) получим:

,

где (8),

и - постоянные величины.

Переход в (8) от к произведён не случайно. Из (6) можно заключить, что алгоритм использует лишь дробное значение смещения частоты. От констант в (8) можно избавиться, поскольку в данном случае важно не абсолютное значение ФП, а относительное, тогда выражение преобразуется к виду

(9).

.

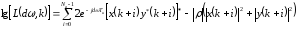Обозначим - корреляционную сумму на интервале длиной , где , и - энергетическая составляющая сигнала на интервале длиной . Тогда (9) имеет вид

(10).

Очевидно, что в момент синхронизации по времени выполняется соотношение , причём для , тогда в момент синхронизации по времени

.

Таким образом, в момент синхронизации ФП (10) имеет вид

(11).

Тот же результат (11) можно получить, рассуждая формально. Довольно часто в алгоритмах, работающих по методу максимального правдоподобия, используют действительную часть комплексной функции правдоподобия, тогда функция (10) преобразуется к виду

.

Тогда условие максимума ФП представляет собой систему уравнений

(12)

Из первого равенства (12) можно сделать вывод, что

(13),

где - целое число.

Поскольку , то . Диапазон измерения аргумента лежит в пределах при реализации алгоритмов определения углов (например, CORDIC), а , т.к. алгоритм использует лишь дробное значение смещения частоты, поэтому в формуле (13) рассматривается лишь случай, когда , т.е. 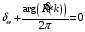. Таким образом, окончательно алгоритм (12) имеет вид

(14).

При реализации алгоритма (14) необходимо выполнять действия в обратном порядке, т.е. найти , при котором . В этом случае можно определить сдвиг частоты .