1.3. Структура передаваемого ofdm - сигнала.
Для синтеза алгоритмов синхронизации необходимо рассмотреть формальное описание передаваемого OFDM-сигнала.
Передаваемый OFDM-символ по свойству преобразования Фурье может быть представлен в виде
,
где
- количество гармоник (поднесущих);
- комплексная амплитуда, определяемая
законом модуляции данных (QAM4,
QAM16,
QAM64
– для стандарта DVB-T).
В дискретном представлении символ без
защитного интервала имеет вид:
,
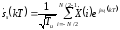где
- длительность символа без защитного
интервала,
;
- период дискретизации;
- расстояние по частоте между гармониками;
- количество отсчетов в БПФ (2048 или 8192
для стандарта DVB-T),
при этом
,
а амплитуды гармоник, не входящих в
,
принимаются равными нулю [6]. После
введения защитного интервала выражение
для символа принимает вид:
,
а показатель
экспоненты
означает, что передача самого символа
начинается в момент времени
,
а до этого
передаётся его периодическое повторение.
На рис. 2 представлена структура
OFDM-символа
в стандарте DVB-T,
стрелкой показана ось времени.
Рис. 2. структура OFDM-символа в стандарте DVB-T.
OFDM - сигнал состоит из последовательности символов и имеет вид:
,
(1)
где
- длительность символа после введения
защитного интервала,
.
1.4. Искажения сигнала, возникающие при передаче и приеме.
Представим сигнал на нулевой частоте на входе схемы синхронизации в виде:
,
где
- информационная составляющая сигнала,
передаваемая на нулевой частоте;
-
задержка передаваемого сигнала,
складывающаяся из времени распространения
в среде, временного сдвига, возникающего
вследствие отклонения частоты
дискретизации
от расчётного значения, а также групповой
задержки, получающейся прохождением
через тракты обработки сигнала. Далее
в формуле
- сдвиг частоты на целое количество
гармоник, где
- расстояние между поднесущими в спектре
сигнала, а
- сдвиг сигнала по частоте на значение,
которое не превосходит
;
-
начальная фаза.
Сдвиг сигнала по
частоте возникает вследствие разности
промежуточных частот приёмника
и передатчика
:
.
1.5. Многолучевое распространение.
В эфире сигнал претерпевает искажения, которые связаны с многолучевым распространением. Импульсная характеристика (ИХ) подобного канала согласно [3] имеет вид
,
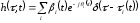(2)
где
,
- амплитуда и фаза импульса, а
- момент появления на приёмном конце
импульса при распространении по одному
из лучей [8,9];
- текущее время (так как параметры канала
могут меняться со временем).
Найдём передаточную
функцию канала как преобразование Фурье
от ИХ, т.е.
,
тогда
.
Таким образом,
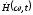представляет собой сумму лучей, амплитуды
и фазы которых зависят от времени и
частоты передаваемого сигнала.
В общем случае
можно отыскать среднее время распространения
,
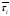которое получается усреднением по всем
с весовыми коэффициентами, пропорциональными
мощности каждого импульса
.
В приближённом случае можно использовать
в качестве
минимальное
,
т.е.
,
так как вследствие затухания в среде
импульс с таким временем распространения
будет иметь максимальную мощность. Так
или иначе, на приёмном конце время
распространения в течение приёма хотя
бы одного символа необходимо принять
постоянным, поэтому возникает ошибка
в определении времени прихода. Более
того, условия приёма могут изменяться
от символа к символу, что выражается в
отклонении
от среднего
,
которое получается усреднением
за некоторое количество символов. Таким
образом, дисперсию
можно найти как
,
где
-
оператор усреднения.