1.3 Фильтры Чебышева

Фильтр Че­бышева нижних частот представляет собой оптимальный полиномиальный фильтр. Он обладает амплитудно-частотной характери­стикой, которая определяется следую­щим образом:

H(j ) = ; (n = 1,2,3…). (1.3)

Параметры  и К — постоянные числа, а С_n является полиномом Чебышева пер­вого рода степени п и имеет вид:

Cn(x) = cos (n arccos x). (1.4)

Амплитудно-частотная характеристика достигает своего наибольшего значения К в тех точках, где С_п равно нулю. Посколь­ку эти точки распределены по полосе про­пускания, то характеристика фильтра Че­бышева содержит пульсации в полосе про­пускания и монотонна в других областях. Размах этих пульсаций определяет пара­метр , а их число степень п. Коэффициент усиления фильтра определяется значением К. На рисунке 4 изображены некоторые ха­рактеристики фильтра Чебышева.

Фильтр Чебышева иногда называют равноволновым фильтром, поскольку все пульсации равны по значению.

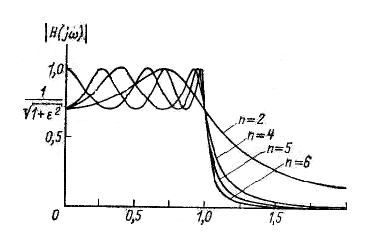
Рисунок 4 – Амплитудно-частотные характеристики фильтра Чебышева нижних частот

Амплитудно-частотная характеристика фильтра Чебышева лучше амплитудно-частотной характеристики Бат­терворта, так как у фильтра Чебышева уже ширина переходной области.

2 Обзор и сравнительная оценка схемных решений активных фильтров

Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие), полосно-пропускающие фильтры, (которые пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы), и полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы).

В зависимости от соотношения значений элементов схемного решения активных фильтров для одних и тех же вариантов схем возможно получение различных амплитудно-частотных характеристик. Наиболее распространенными являются так называемые фильтры Баттерворта и Чебышева.

Частотная характеристика фильтра Баттерворта в пределах полосы пропускания весьма близка к равномерной и ее называют максимально плоской. Наклон переходного участка характеристики фильтра Баттерворта равен 6 дБ/октава на порядок. Используется фильтр Баттерворта в тех случаях, когда желательно иметь одинаковый коэффициент усиления для всех частот в полосе пропускания. Характеристика фильтра Чебышева имеет волнообразные зубцы в полосе пропускания и равномерна в полосе подавления. Количество зубцов характеристики в полосе пропускания тем больше, чем выше его порядок. Амплитуда зубцов может быть задана при конструировании фильтра и обычно устанавливается на уровне 0,1; 0,5; 1; 2 и 3 дБ, причем увеличение допустимой амплитуды зубцов позволяет получить более крутой наклон характеристик фильтра па переходном участке.

Для создания активных фильтров в настоящее время разработано большое количество схем, каждая из которых обладает как достоинствами, так и недостатками.

Существует много способов построения активных фильтров низких частот Баттерворта и Чебышева.

Одна из наиболее простых схем активных фильтров  схема с многопетлевой обратной связью (МОС) и бесконечным коэффициентом усиления. Эта схема реализует уравнение с инвертирующим коэффициентом усиления – К.

Рисунок 5 – Схема фильтра нижних частот с МОС

Из-за своей относительной простоты фильтр с МОС является одним из наиболее популярных типов фильтров с инвертирующим коэффициентом усиления. Он обладают также определёнными преимуществами, а именно хорошей стабильностью характеристик и низким выходным полным сопротивлением; таким образом, его можно сразу соединять каскадно для реализации фильтров более высокого порядка. Недостаток схемы состоит в том, что невозможно достичь высокого значения добротности Q без значительного разброса значений элементов и высокой чувствительностью к их изменению.

Широко распространена схема фильтра нижних частот, реализующая неинвертирующий (положительный) коэффициент усиления. Эта схема иног­да называется фильтром на ИНУН, поскольку операционный усилитель и два подсоединенных к нему резистора образуют источник напряжения, управляемый напряжением (ИНУН). Фильтр на ИНУН позволяет добиться не инвертирующего коэффициента усиления при минимальном числе элементов. Он обладает низким выходным сопротивлением, небольшим разбросом значений элементов и возможностью получения относительно высоких значений коэффициента усиления. Однако подобно фильтру с МОС фильтр на ИНУН должен использоваться для значений добротности Q  0.

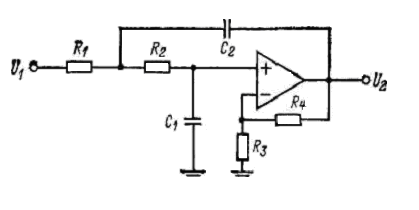
Рисунок 6 – Схема фильтра нижних частот на ИНУН

Хорошо известны схемы активных фильтров на основе биквадратной схемы. Хотя эта схема содержит больше элементов, чем схемы с МОС и на ИНУН, по характеристике она лучше и имеет преимущества за счёт простоты настройки и лучшей стабильности. Сравнительно просто реализуется значение добротности Q вплоть до 100, и относительно легко формируются фильтры высокого порядка на основе каскадного соединения нескольких биквадратных звеньев.