Расчет выпрямителя с активно-индуктивной нагрузкой

При расчете выпрямителя исходными данными являются: номинальное выпрямленное напряжение ; максимальный и минимальный токи нагрузки , ; мощность ; номинальное напряжение сети ; относитель-ные отклонения напряжения сети в сторону повышения и понижения , ; частота тока питающей сети .

1. Выбираем схему выпрямления и определяем m (рис. 1, а-д).

Рис. 1. Схемы выпрямления для однофазной сети переменного тока:

а – однополупериодная; б – двухполупериодная с выводом средней точки;

в – мостовая; г – удвоения напряжения; д – умножения напряжения

2. Определяем параметры вентилей , , . Напряжение находим по максимальному значению выпрямленного напряжения (табл. 1 и 2) .

Таблица 1

Основные параметры схем при работе на активную нагрузку (рис. 1)

Параметры	Схема выпрямления
	Однополупериодная	Двухполупериодная	Однофазная мостовая
	2,22	1,11	1,11
	3,14	3,14	1,57
	1	0,5	0,5
	3,14	1,57	1,57
	1,57	0,785	0,785
	1,57	0,785	1,11
	1,21	1,11	1,11
	3,49	1,74	1,23
	2,69	1,23	1,23
	3,09	1,48	1,23
	1,57	0,67	0,67
	1	2	2

Производим выбор вентилей по приложению 1 и выписываем их параметры , или , или . При выборе вентилей необходимо, чтобы обратное напряжение , приложенное к вентилю, было меньше максимально допустимого обратного напряжения для выбранного типа вентиля .

Таблица 2

Основные параметры схем при работе на индуктивную нагрузку (рис. 1)

Параметры	Схема выпрямления
	Двухполупериодная	Однофазная мостовая
	1,11	1,11
	3,14	1,57
	0,5	0,5
	1	1
	0,707	0,707
	0,707	1
	1	1
	1,57	1,11
	1,11	1,11
	1,34	1,11
	0,67	0,67
	2	2

Действующее значение тока вентиля должно быть меньше значения тока , указанного в справочных данных. Если приведено значение , то следует иметь в виду, что

3. Определяем активное сопротивление и индуктивность рассеяния обмоток трансформатора:

, (1)

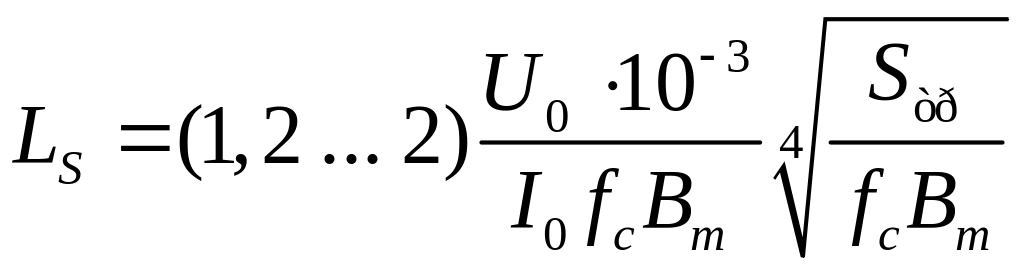, (2)

где j – плотность тока в обмотках трансформатора, ;

B – амплитуда магнитной индукции, Тл.

Плотность тока j и амплитуда магнитной индукции B определяются по габаритной мощности трансформатора из графиков на рис. 2 - 5.

Рис. 2. Зависимости при для стержневых и

броневых магнитопроводов: 1 – сталь 3412; 2, 3 – сталь 3423

Рис. 3. Зависимости при для кольцевых трансформаторов (магнитопровод из 34НКМП): 1 – толщина ленты 0,05 мм; 2 – толщина ленты 0,02 мм

Рис. 4. Зависимости при для кольцевого трансформатора; материал сердечника 2000НМ1 (2000НМ3)

Рис. 5. Зависимости при

Определяем .

4. Определяем напряжение холостого хода выпрямителя:

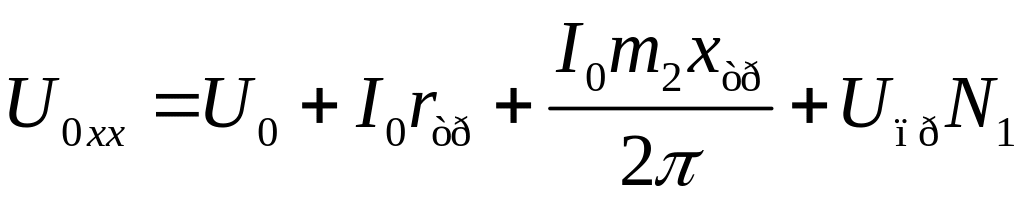, (3)

где – число вентилей, включенных последовательно.

Если выпрямитель включен в сеть непосредственно без трансформа-тора, то в (3) , .

5. Определяем по , , (табл. 1, 2) параметры трансформатора , , , , , . Исходными данными для расчета трансформатора являются: – номинальное напряжение сети; – напряжение вторичной обмотки трансформатора при холостом ходе; , – действующие значения токов вторичной и первичной обмоток и – габа-ритная мощность трансформатора.

6. Определяем напряжение холостого хода выпрямителя при макси-мальном напряжении сети:

. (4)

Уточняем обратное напряжение по (табл. 1, 2) и проверяем, правильно ли выбраны вентили по значению обратного напряжения.

7. Определяем напряжение на выходе выпрямителя при минимальном напряжении сети . Из табл. 1, 2 находим частоту основной гармоники пульсации выпрямленного напряжения и коэффициент пульсации . Из (2.7) определяем угол перекрытия фаз и по рис. 6 уточняем .

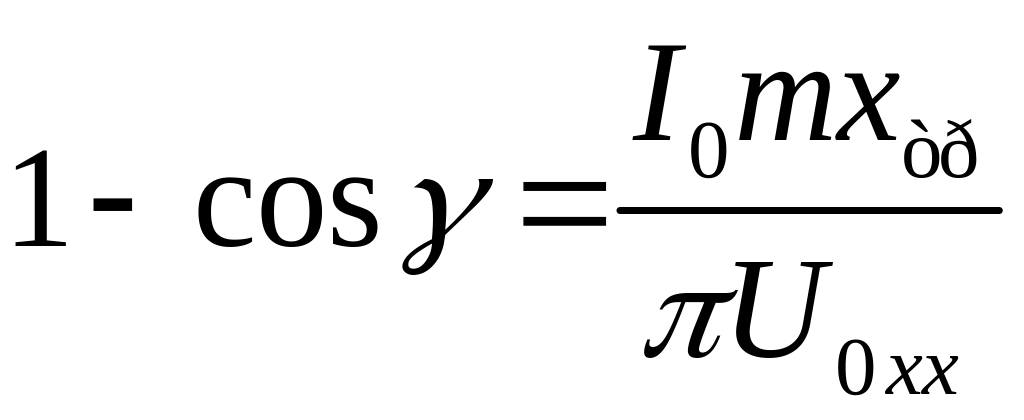, (5)

где ;

– индуктивность рассеяния обмоток трансформатора.

Рис. 6. Зависимости коэффициента пульсации от угла γ

8. Определяем внутреннее сопротивление выпрямителя при изменении тока нагрузки от 0 до максимального значения:

.

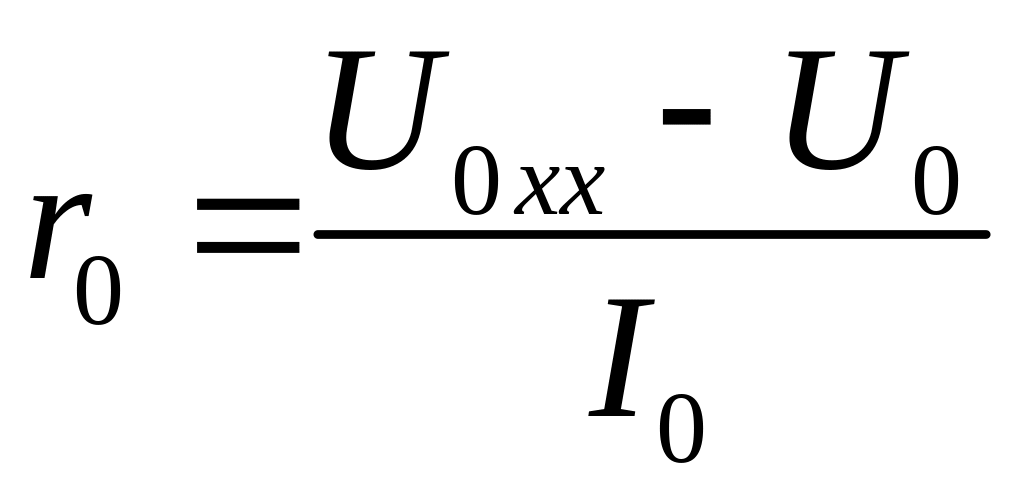9. Рассчитываем коэффициент полезного действия выпрямителя по формуле:

,

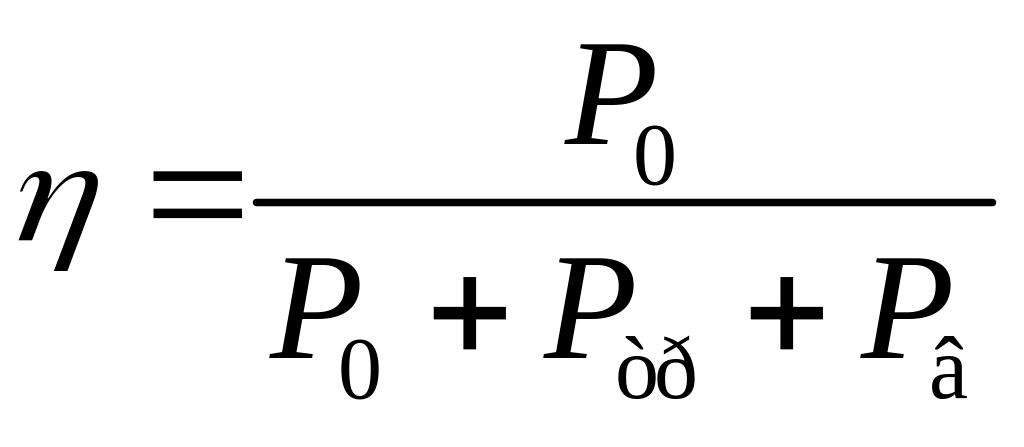где – потери мощности в трансформаторе, определяемые после его

расчета;

– потери в вентилях;

N – общее число вентилей.