
Нуруллин К.В. гр. ПИ-107сз
Вариант 24
Задача №№1-3.
Три предприятия данного экономического района могут производить некоторую однородную продукцию в количествах соответственно равных А1, А2, А3 единиц. Эта продукция должна быть поставлена пяти потребителям в количествах, соответственно равных В1, В2, В3, В4, В5 единиц. Затраты связанные с производством и доставкой единицы продукции, задаются матрицей С.
Составить план прикрепления потребителей к поставщикам, решить задачу тремя методами, сделать вывод о том какой из полученных планов является оптимальным.
А1=140, А2=260, А3=150, В1=120, В2=130, В3=90, В4=50, В5=160;
С
=
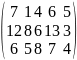 .
.
ПО МЕТОДУ СЕВЕРО-ЗАПАДНОГО УГЛА
Функция отправления |
Пункты назначения |
|||||
В1 |
В2 |
В3 |
В4 |
В5 |
Запас |
|
А1 |
7 120 |
1 20 |
4 |
6 |
5 |
140/20/0 |
А2 |
12 |
8 110 |
6 90 |
13 50 |
3 10 |
260/150/60/10/0 |
А3 |
6 |
5 |
8 |
7 |
4 150 |
150/0 |
Потребности |
120/0 |
130/110/0 |
90/0 |
50/0 |
160/150/0 |
|
Мы можем полностью удовлетворить потребность А1В1, т.к. запас А1=180. Исключаем столбец В1, т.к. потребности полностью удовлетворены, и будем считать запасы А1=20.
Мы можем частично удовлетворить потребность А1В2, запасы А1=20. Исключаем строку А1, т.к. запасы исчерпаны.
Мы можем полностью удовлетворить потребность А2В2, т.к. запас А2=260. Исключаем столбец В2, т.к. потребности полностью удовлетворены, и будем считать запас А2=150.
Мы можем полностью удовлетворить потребность А2В3, т.к. запас А2=150. Исключаем столбец В3, т.к. потребности полностью удовлетворены, и будем считать запас А2=60.
Мы можем полностью удовлетворить потребность А2В4, т.к. запас А2=60. Исключаем столбец В4, т.к. потребности полностью удовлетворены, и будем считать запас А2=10.
Мы можем частично удовлетворить потребность А2В5, т.к. запас А2=10. Исключаем строку А2, т.к. запасы исчерпаны.
Мы можем полностью удовлетворить потребность А3В5, т.к. запасы А3=150. Исключаем строку А3 и столбец В5, т.к. потребности полностью удовлетворены и запасы исчерпаны.
Х
=
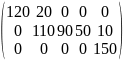
F = 120*7 + 20*1 + 110*8 + 90*6 + 50*13 + 10*3 + 150*4 = 3560
Затраты равны 3560.
По методу наименьшего элемента
Функция отправления |
Пункты назначения |
|||||
В1 |
В2 |
В3 |
В4 |
В5 |
Запас |
|
А1 |
7 |
1 130 |
4 10 |
6 |
5 |
140/10/0 |
А2 |
12 |
8 |
6 80 |
13 20 |
3 160 |
260/100/20/0 |
А3 |
6 120 |
5 |
8 |
7 30 |
4 |
150/30/0 |
Потребности |
120/0 |
130/0 |
90/80/0 |
50/20/0 |
160/0 |
|
Заполняем ячейку А1В2, т.к. там наименьший тариф (1). Мы можем полностью удовлетворить потребность А1В2, запас А1=140. Исключаем столбец В2, т.к. потребности полностью удовлетворены, и будем считать запасы А1=10.
Заполняем ячейку А2В5, т.к. там наименьший тариф (3). Мы можем полностью удовлетворить потребность А2В5, запас А2=260. Исключаем столбец В5, т.к. потребности полностью удовлетворены, и будем считать запасы А2=100.
Заполняем ячейку А1В3, т.к. там наименьший тариф (4). Мы можем частично удовлетворить потребность А1В3, т.к. запас А1=10. Исключаем строку А1, т.к. запасы исчерпаны.
Заполняем ячейку А2В3, т.к. там наименьший тариф (6). Мы можем полностью удовлетворить потребность А2В3, запас А3=100. Исключаем столбец В3, т.к. потребности полностью удовлетворены, и будем считать запасы А2=20.
Заполняем ячейку А3В1, т.к. там наименьший тариф (6). Мы можем полностью удовлетворить потребность А3В1, запас А3=150. Исключаем столбец В1, т.к. потребности полностью удовлетворены, и будем считать запасы А3=30.
Заполняем ячейку А3В4, т.к. там наименьший тариф (7). Мы можем частично удовлетворить потребность А3В4, запас А3=30. Исключаем строку А3, т.к. запасы исчерпаны.
Заполняем ячейку А2В4, т.к. там наименьший тариф (13). Мы можем полностью удовлетворить потребность А2В4, запас А2=20. Исключаем строку А2 и столбец В4, т.к. запасы исчерпаны и потребности полностью удовлетворены.
Х
=
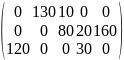
F = 130*1 + 10*4 + 80*6 + 20*13 + 160*3 + 120*6 + 30*7 = 2320
Затраты равны 2320.
