Задачи для активного обучения

Задача 3.1.

Исключить рекурсию из следующего рекурсивного определения:

.

Решение. Имеем , ,

, ,

и т. д.

Вероятно, функция имеет вид .

Чтобы доказать справедливость этой формулы, покажем, что данная функция удовлетворяет рекурсивному соотношению: , .

Таким образом, функция найдена верно.

Задача 3.2.

Исключить рекурсию из рекурсивного соотношения:

.

Решение. Рассматриваем следующие равенства ,

, ,

,

Можно предположить, что

Проверим выполнение рекурсивных соотношений: ,

.

Задача 3.3.

Для функции найти задающие ее рекурсивные соотношения.

Решение. Вычислим несколько первых значений

, ,

, ,

и т.д.

Можно предположить следующее: .

Для доказательства применим индукцию:

- очевидно, что ;

- допустим и покажем, что . Действительно

Задачи для самостоятельного решения

1. Найти для приведенных ниже рекурсивных функций:

а) б) в)

г) д) е)

2. Найти для следующих рекурсивных функций:

а) б)

в) г)

3. Найдите явные выражения для , исключив рекурсию из следующих определений:

а) б) в)

г) д) е)

4. Докажите, что удовлетворяет рекурсивному определению:

а) , б) ,

в) , г)

Ответы

1. а)

б)

в)

г)

д)

е)

2. а)

б)

в)

г)

3. а) , б) , г) , е) .

Раздел 4. Элементы теории графов. Деревья Теоретические сведения

Теория графов является важным разделом математики. Графами удобно изображаются сети коммуникаций, дискретные многошаговые процессы, системы бинарных отношений, химические структурные формулы, различные схемы и диаграммы и др.

Граф – это пара, состоящая из произвольного (не обязательно конечного) множества объектов и некоторой совокупности пар этих объектов. Элементы множества называются вершинами графа, а пары вершин (элементы множества ) – его ребрами.

Обычно конечный граф изображают на плоскости: вершинам сопоставляют точки, а ребрам – линии, соединяющие эти точки.

Если - ребро, то вершины называются концами ребра. Ребро называют также инцидентным к вершинам и , вершины при этом называются смежными (обозначают ~ ).

Пример. Граф с множеством вершин и множеством ребер может быть изображен, как показано на рис. 4.1.

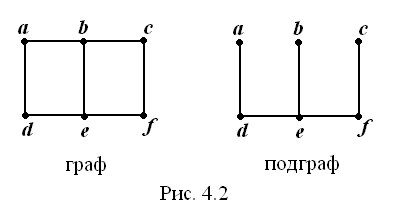
Граф называется подграфом графа , если , .

На рис. 4.2 изображены граф и его подграф.

Выделяют следующие типы графов (причем возможны сочетания понятий, см. рис. 4.3):

мультиграфы (в графе допускаются более одного ребра между двумя вершинами, т. н. «кратные» ребра);

псевдографы (разрешены «петли» - ребра, которые соединяют вершину саму с собой);

орграфы или ориентированные графы (пары вершин, образующие ребра графа, упорядочены).

Степенью вершины называется число , равное количеству ребер, инцидентных этой вершине. Вершина степени 0 называется изолированной. Сумма степеней вершин графа всегда четная.

Степенью выхода вершины орграфа называется количество ребер, для которых является начальной вершиной (обозн. ). Если , то вершина называется источником.

Степенью входа вершины орграфа называется количество ребер, для которых является конечной вершиной (обозн. ). Если , то вершина называется стоком.

Путь (маршрут) в графе – это совокупность ребер, которые объединены вместе вершинами так, что вдоль них можно двигаться по графу. Путь длины имеет ребер. Простым называется путь, в котором нет повторяющихся вершин.

Граф называется связным, если имеется путь между двумя его различными вершинами.

Циклом называется путь ненулевой длины, соединяющий вершину саму с собой и не содержащий повторяющихся ребер.

Цикл, соединяющий вершину саму с собой, называется простым циклом, если он не содержит повторяющихся вершин, кроме .

n-цикл содержит ребер и различных вершин.

Граф называется полным, если любые две его вершины соединены ребром. Полный граф с вершинами обозначается через .

На рис. 4.4 показаны,

соответственно, полные графы .

Дерево – это граф без циклов.

Лес – это граф, компонентами которого являются деревья.

Если для любых двух вершин графа существует единственный путь из вершины в вершину , то - дерево.

Дерево и названо «деревом», поскольку будучи нарисованным, выглядит как перевернутое «вверх ногами» дерево (см. рис. 4.5).

Вершина в самой верхней части рис. 4.5 называется корнем дерева. Если корень дерева определен, оно называется корневым деревом.

Вершины степени 1 называют листьями, другие вершины называются внутренними вершинами.

Высотой дерева называется величина самого длинного пути от корня дерева до листа.

В каждом дереве число вершин на единицу больше числа ребер : .

Пусть - граф. Цикл, который включает все ребра и вершины графа , называется эйлеровым циклом.

Путь, который включает каждое ребро графа только один раз, называется эйлеровым путем.

Г раф с более чем одной вершиной имеет эйлеров цикл тогда и только тогда, когда он связный и каждая его вершина имеет четную степень.

П ример. Граф на рис. 4.6 имеет эйлеров цикл, поскольку степень каждой вершины четная, а граф на рис. 4.7 не имеет эйлерова цикла, т. к. степени вершин и - нечетные.

Если эйлеров путь не является эйлеровым циклом, то его называют собственным эйлеровым путем.

Граф имеет собственный эйлеров путь тогда и только тогда, когда он связный и ровно две его вершины имеют нечетную степень (см. рис. 4.8).

Ориентированный граф имеет эйлеров цикл тогда и только тогда, когда он связный и степень входа каждой вершины равна ее степени выхода (см. рис. 4.9).

Матрицей инцидентности графа называется матрица , элемент которой равен 1, если -ая вершина инцидента -ому ребру, и равен 0 в противном случае.

Будем считать, что вершины и ребра графа пронумерованы. Строки матрицы обозначены вершинами графа, а столбцы обозначены ребрами графа.

Степень вершины равна сумме элементов строки.

По матрице инцидентности нельзя восстановить ориентированный граф. Однако, такую возможность обеспечивает матрица смежности.

Матрицей смежности орграфа графа называется матрица , элемент которой равен 1, если имеется ориентированное ребро из -ой вершины в -ую вершину, и равен 0 в противном случае.

Матрицы инцидентности и смежности удобно хранить в памяти компьютера, т. к. в качестве элементов они содержат только 1 или 0, но при этом полностью описывают граф.