Задачи для самостоятельного решения
Является ли действие
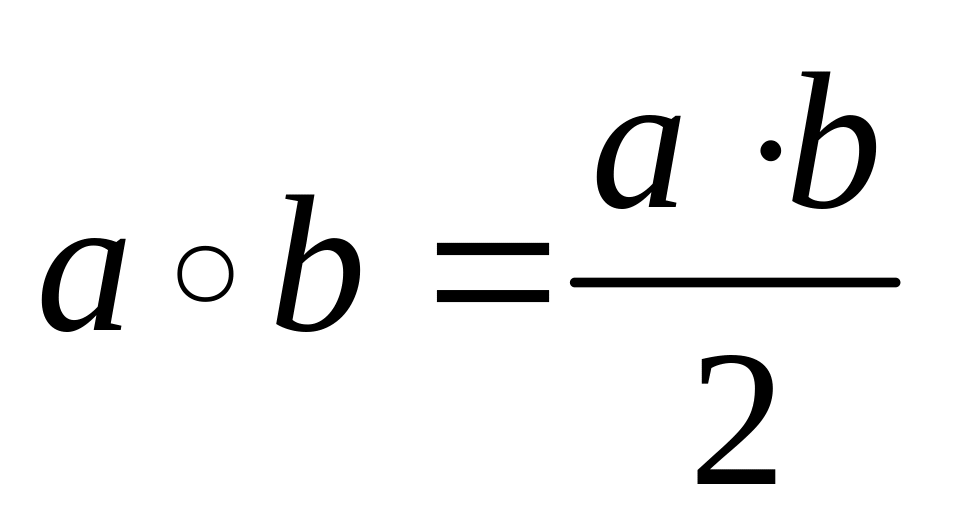бинарной алгебраической операцией на
Q+?Проверьте, какие из нижеприведенных множеств являются группами относительно указанных операций:
а) множество целых чисел, кратных любому заданному натуральному числу , относительно сложения;
б) множество Q+ относительно умножения;
в) множество рациональных чисел Q относительно умножения;
г)
множество чисел вид
а
относительно сложения, если a
и
b
-
любые рациональные числа;
д) множество многочленов одной и той же степени n от одного аргумента относительно сложения;
е) множество квадратных матриц n-го порядка M(n, R) относительно сложения;
ж) множество квадратных матриц n-го порядка M(n, R) относительно умножения;
з) множество матриц n-го порядка с определителем, равным 1 относительно умножения;
и) множество матриц n-го порядка с определителем, равным 1 относительно сложения;
к)
множество
относительно
операции
.
3. Докажите, что множество четных чисел является подгруппой аддитивной группы целых чисел.
Ответы
Является; 2. а) является группой; б) является группой; в) не является группой; г) является группой; д) не является группой; е) является группой; ж) не является группой; з) является группой; и) не является группой (сумма двух матриц с определителем 1не является матрицей с определителем 1); к) является группой (нейтральный элемент 2).
Литература
1. Андерсон, Джеймс Дискретная математика и комбинаторика – М.: Издательский дом «Вильямс», 2003. - 960 с.
2. Гаврилов, Г. П. Задачи и упражнения по дискретной математике: Учеб пособие. - 3-е изд., перераб. – М.: Физматлит, 2004. – 416 с.
3. Упражнения по теории групп: Методические указания / Сост.: Н.П. Пучков, В.В. Скоморохов. Тамбов: Изд-во Тамб.гос.техн. ун-та, 2005.
4. Сборник задач по высшей математике. 2 курс/ [К.Н.Лунгу и др.]; под ред. С.Н. Федина. – 5-е изд. – М.: Айрис-пресс, 2007. -592 с.
Содержание
Введение…………………………………………………………………. |
2 |
Раздел 1. Основы математической логики.…………………………… |
3 |
Раздел 2. Теория множеств…………………………………………….. |
13 |
Раздел 3. Алгоритмы и рекурсия………………………………………. |
18 |
Раздел 4. Элементы теории графов. Деревья…………………………. |
23 |
Раздел 5. Элементы комбинаторики…………………………………... |
31 |
Раздел 6. Алгебраические структуры………………………………….. |
36 |
Литература…………………………………….………………………… |
40 |