2.3. Эффект Комптона

Эффект Комптона состоит в увеличении длины волны коротковолнового (рентгеновского и гамма-) излучения, происходящем при его рассеянии легкими атомами (вернее, электронами, входящими в состав легких атомов).

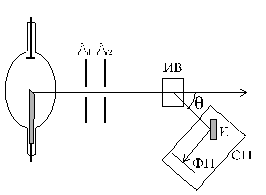
Впервые это явление наблюдалось американским физиком А.Комптоном в 1922 г. Схема его установки показана на рис.2.6. Источником рентгеновских лучей служила рентгеновская трубка, работающая в режиме излучения характеристического спектра. Узкий пучок монохроматического рентгеновского излучения выделялся диафрагмами Д₁, Д₂ и рассеивался на исследуемом веществе ИВ. Для исследования спектрального состава рассеянного излучения оно после прохождения ряда диафрагм попадало на кристалл К рентгеновского спектрографа Сп, а затем на фотопластинку ФП. Комптон исследовал рассеяние на веществах, состоящих из легких атомов (парафин, графит, бор и др.).

Рис. 2.6.

Оказалось, что в рассеянном излучении, наряду с исходной длиной волны , появляется излучение с длиной волны >. При этом изменение длины волны = для исследованных веществ не зависит от вида рассеивающего вещества и длины падающей волны . Оно пропорционально квадрату синуса половины угла рассеяния  т.е.

, (2.5)

где _K  2,43^.10^-12 м  постоянная, называемая комптоновской длиной волны электрона.

Теория эффекта Комптнона. Эффект Комптона можно объяснить, рассматривая его как процесс упругого столкновения рентгеновских фотонов с веществом. При этом необходимо использовать тот факт, что в опытах Комптона все легкие атомы (водород, бор, углерод, алюминий и т.д.) ведут себя одинаково. Это позволяет сделать предположение, что процесс рассеяния сводится к упругому столкновению фотона с электронами атома. Поскольку в легких атомах связь электрона с ядром слаба, то в первом приближении можно рассматривать рассеяние фотонов на практически свободных электронах. При взаимодействии фотона и электрона должны выполняться законы сохранения импульса и энергии.

Пусть на покоящийся свободный электрон налетает фотон с энергией h и импульсом p=h /c. Кинетическая энергия электрона Т после взаимодействия (с учетом релятивистских эффектов) может быть записана как T=mc² m₀ c², где m₀  масса покоя электрона и . Закон сохранения энергии имеет вид

или

, (2.6)

где h  энергия рассеянного фотона.

Рис.2.7

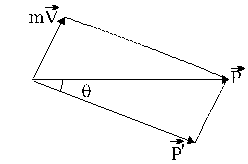
Импульсы фотона до и после рассеяния равны соответственно: p=h/c и p=h/c; импульс электрона после столкновения mV. Согласно закону сохранения импульса (см. рис.2.7). Воспользовавшись для импульсов теоремой косинусов, получим

или

. (2.7)

Выделим в (2.6) слагаемое mc², возведем его в квадрат и перепишем его в виде

.

Вычитая из него (2.7), получаем

. (2.8)

Из связи массы покоя m_o и массы m электрона имеем

,

с учетом этого выражение (2.8) преобразуется к следующему виду

. (2.9)

Введем в (2.9) вместо частоты  длину волны , воспользовавшись соотношениями c/, c/, и , тогда

.

И окончательно

. (2.10)

Полученное выражение совпадает с экспериментальной формулой, причем с большой точностью выполняется условие ^.