4. Основы квантовой механики

4.1. Волны де Бройля

В 1923 г. французский физик Луи де Бройль высказал гипотезу о том, что поскольку свет ведет себя в одних случаях как волна, в других  как частица, то и объекты природы, которые мы считаем частицами (элементарные частицы, атомы, молекулы и т.д.), могли бы обладать волновыми свойствами. Де Бройль предположил, что длина волны, отвечающая материальной частице, связана с ее импульсом так же, как в случае фотона, т.е. соотношением (2.3): p=h/. Иначе говоря, любой частице с массой m, которая движется со скоростью V, соответствует волна, для которой длина волны

. (4.1)

Величину  называют дебройлевской длиной волны частицы. Дебройлевская длина волны обычных тел слишком мала, чтобы ее можно было обнаружить. Так длина волны шарика массой m=10^-3 кг, движущегося со скоростью V=10² м/с составляет всего 6,62^.10^-33 м. Очевидно, что такая величина не поддается измерению.

Другое дело, если речь идет об элементарных частицах. Так как масса частицы входит в знаменатель формулы (4.1), то частице с очень малой массой соответствует достаточно большая длина волны. Легко посчитать, что электронам, ускоренным разностью потенциалов 100 В, соответствует длина волны 0,12 нм. Хотя это очень короткие волны, но их можно обнаружить экспериментально: межатомные расстояния в кристалле того же порядка (0,1 нм), и регулярно расположенные атомы кристалла можно использовать в качестве дифракционной решетки, как и в случае рентгеновского излучения.

Дифракция электронов при их рассеянии на кристаллах была обнаружена еще до появления гипотезы де Бройля (в 1921-1923 гг.), но это явление долго оставалось непонятным, пока не было истолковано как результат интерференции волн де Бройля, рассеянных различными атомами.

Рис.4.1

Наличие волновых свойств у частиц (электронов) экспериментально было убедительно подтверждено в 1927 г. в опытах американских физиков Дэвиссона и Джермера. В этих опытах (схема опыта на рис.4.1) наблюдалось рассеяние параллельного пучка моноэнергетических электронов, создаваемого электронной пушкой ЭП, на монокристалле никеля. Рассеянные электроны улавливались коллектором Кл, соединенным с гальванометром G. По показаниям гальванометра можно было судить об интенсивности пучка электронов, рассеянных в различных направлениях. Оказалось, что при постоянном угле скольжения =const при изменении ускоряющего напряжения U между катодом К и анодом А электронной пушки ток через гальванометр I периодически зависел от (рис.4.2). Исходя из гипотезы де Бройля, это соотношение легко получается аналитически.

Действительно, ,

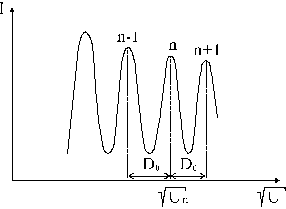Рис.4.2

^{откуда , где V  скорость электронов. Из (4.1) следует, что таким электронам соответствует длина волны}

^.

^{Если электрон обладает волновыми свойствами, то дифракционный максимум (максимум тока коллектора) должен наблюдаться при выполнении условия Брэгга-Вульфа}

^{(n=0,1,2,...).}

Учитывая это, получим

^{, откуда ,}

т.е. соответствует опытным фактам.

Позднее дифракция электронов наблюдалась также при их прохождении сквозь тонкую поликристаллическую металлическую фольгу. При этом наблюдаемая дифракционная картина была аналогична случаю дифракции рентгеновских волн. Более того, вычисления постоянной кристаллической решетки из рентгенограммы и электронограммы приводили к одинаковым значениям.

Волновые свойства наблюдались не только у электронов, но и у более тяжелых частиц  протонов, нейтронов, легких атомов. Таким образом, экспериментально было доказано, что волновые явления свойственны всем частицам независимо от их природы и строения.

В настоящее время волновые свойства частиц получили обширные научно-технические применения: в электронной микроскопии, электронографии, нейтронографии т.д.