
МатАн. ОТВЕТЫ 2017
.docx-
Модуль действительного числа и его свойства.
-
Модуль числа – абсолютная положительная величина числа.
Свойства
-
|a|=|-a|
-
|a
 b|=|a|
b|=|a| |b|
|b| -
Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b, то есть,

-
Модуль суммы двух чисел меньше суммы модулей этих чисел. |a+b|
 |a|+|b|
|a|+|b|
-
Предел числовой последовательности.
-
Число A
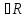 называется
пределом числовой последовательности
называется
пределом числовой последовательности
 , если
, если

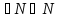


Пишут:

-
Предел функции, теорема единственности предела.
-
(Коши)
-
Число
 называется
пределом функции
называется
пределом функции
 в
точке
в
точке
 ,
если:
,
если:
-
Функция
 определена
в некоторой проколотой окрестности
точки
определена
в некоторой проколотой окрестности
точки
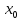
-
выполняется условие:


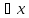


-
(Гейне)
-
Число
 называется
пределом функции
называется
пределом функции
 в
точке
в
точке
 ,
если:
,
если:
-
Функция
 определена
в некоторой проколотой окрестности
точки
определена
в некоторой проколотой окрестности
точки

-
Для любой последовательности точек
 из
некоторой проколотой окрестности точки
из
некоторой проколотой окрестности точки
 , имеющей своим пределом
, имеющей своим пределом
 , соответствующая последовательность
значений функции
, соответствующая последовательность
значений функции
 имеет своим пределом число А
имеет своим пределом число А
-
Если функция имеет предел в точке, то этот предел единственный.
-
Ограниченность функции, имеющей конечный предел.
-
Если функция имеет конечный предел в точке, то она ограничена в некоторой проколотой окрестности этой точки.
-
Предел суммы, произведения и частного функций.
-
Предел суммы

-
Предел произведения

-
Предел частного
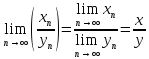
-
Предельный переход в неравенствах.
Пусть
в некоторой проколотой окрестности
точки
 выполняется
неравенство
выполняется
неравенство
f
(x)
 g(x)
.
Тогда
g(x)
.
Тогда
 ,
если
пределы существуют.
,
если
пределы существуют.
-
Свойства бесконечно больших и бесконечно малых величин. Сравнение бесконечно малых.
-
Функция
 называется
бесконечно
малой
при
называется
бесконечно
малой
при
 если
если

-
Функция
 называется
бесконечно
большой
при
называется
бесконечно
большой
при
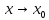 если
если

-
Свойства
-
Произведение бесконечно малой при
 на
функцию, ограниченную в некоторой
проколотой окрестности точки
на
функцию, ограниченную в некоторой
проколотой окрестности точки
 ,
является
бесконечно малой при
,
является
бесконечно малой при
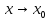
-
Если
 –
бесконечно малая при
–
бесконечно малая при
 , не принимающая значение 0
в некоторой проколотой окрестности
точки
, не принимающая значение 0
в некоторой проколотой окрестности
точки
 ,
то
,
то
 –
бесконечно большая при
–
бесконечно большая при

-
Если
 –
бесконечно большая при
–
бесконечно большая при
 , не принимающая значение 0
в некоторой проколотой окрестности
точки
, не принимающая значение 0
в некоторой проколотой окрестности
точки
 ,
то
,
то
 –
бесконечно малая при
–
бесконечно малая при

-
Функция
 является бесконечно малой более высокого
порядка по сравнению с
является бесконечно малой более высокого
порядка по сравнению с
 при
при
 , если
, если

-
Непрерывность основных элементарных и элементарных функций. Классификация точек разрыва.
-
основные элементарные функции:
-
степенные функции

-
показательные функции

-
логарифмические функции

-
тригонометрические функции




-
круговые (обратные тригонометрические) функции
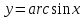



-
Функция называется элементарной, если она может быть представлена через основные элементарные функции с помощью конечного числа операций
-
Основные элементарные функции непрерывны в области определения.
-
Точка, в которой функция не является непрерывной, называется точкой разрыва.
-
1) Функция f (x) имеет в точке xo устранимый разрыв, если выполняются условия 1–2, но не выполняется условие 3.
Точка а называется точкой устранимого разрыва функции, если предел функции в этой точке существует, но в точке а функция либо не определена, либо ее значение не равно пределу в этой точке
-
2) Функция f (x) имеет в точке xo разрыв I рода («разрыв скачка»), если выполняется только условие 1.
Точка а называется точкой разрыва первого рода функции, если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы.
-
3) Функция f (x) имеет в точке xo разрыв II рода, если условие 1 не выполняется.
Точка а называется точкой разрыва второго рода функции. Точка а называется точкой устранимого разрыва функции, если в этой точке функция не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
-
Теорема Коши о промежуточных значениях функции, непрерывной на отрезке.
Если функция f (x) непрерывна на промежутке X и её значения
f(a)=A, f(b)=B, то для любого числа C, заключённого между A и
B,
существует точка x0 X,
в которой значение f(x0)=C
X,
в которой значение f(x0)=C
-
Теорема Вейерштрасса об ограниченности функции, непрерывной на отрезке.
-
Если функция непрерывна на отрезке, то она ограничена на нём.
-
Теорема Вейерштрасса о достижении наибольшего и наименьшего значений функции, непрерывной на отрезке.
-
Если функция непрерывна на отрезке, то среди её значений на этом отрезке есть наибольшее и наименьшее
-
Производная и дифференциал, дифференцирование функций.
-
Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению её аргумента.
-
дифференциал функции y = f(x) в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение
 .
. -
Дифференцирование произведения функций.

-
Дифференцирование сложной функции.

-
Связь непрерывности и дифференцируемости функции.
Если функция y=f(x) дифференцируема на некотором интервале, то она и непрерывна на этом интервале. Но обратное утверждение НЕВЕРНО.
