§4. Квадратичні форми в евклідовому просторі.

1. Приєднані лінійні перетворення. Лінійне перетворення евклідового простору називається приєднаним для квадратичної форми , якщо воно самоспряжене і

. (12)

Теорема 1. Якщо квадратична форма має приєднане лінійне перетворення , то його матриця в будь-якому ортонормованому базисі збігається з матрицею квадратичної форми в тому самому базисі.

Доведення. Нехай – який-небудь ортонормований базис евклідового простору , – довільний вектор цього простору, , , і нехай квадратична форма в базисі має матрицю , тобто . Нехай – приєднане лінійне перетворення з матрицею в тому самому базисі. Тоді , і рівність (12) набуває вигляду

,

або

.

Оскільки – довільний вектор, то , тобто . Теорему доведено.

Теорема 2. Кожна квадратична форма має приєднане лінійне перетворення, до того ж єдине.

Доведення. Виберемо який-небудь ортонормований базис і розглянемо лінійне перетворення , матриця якого у вибраному базисі збігається з матрицею квадратичної форми у тому самому базисі. Оскільки матриця як матриця квадратичної форми симетрична, то перетворення самоспряжене. Далі,

і звідси,

,

тобто лінійне перетворення приєднане для квадратичної форми .

Якщо – інше приєднане лінійне перетворення, то за теоремою 1, його матриця збігається з матрицею лінійного перетворення , що рівнозначно тому, що .

Теорема 3. Для кожної квадратичної форми в евклідовому просторі існує ортонормований базис з власних векторів приєднаного лінійного перетворення , в якому вона має канонічний вигляд.

Доведення. За теоремою про базис з власних векторів самоспряженого лінійного перетворення попереднього розділу, для приєднаного лінійного перетворення існує ортонормований базис з власних векторів цього перетворення. В цьому базисі матриця лінійного перетворення має діагональний вигляд:

,

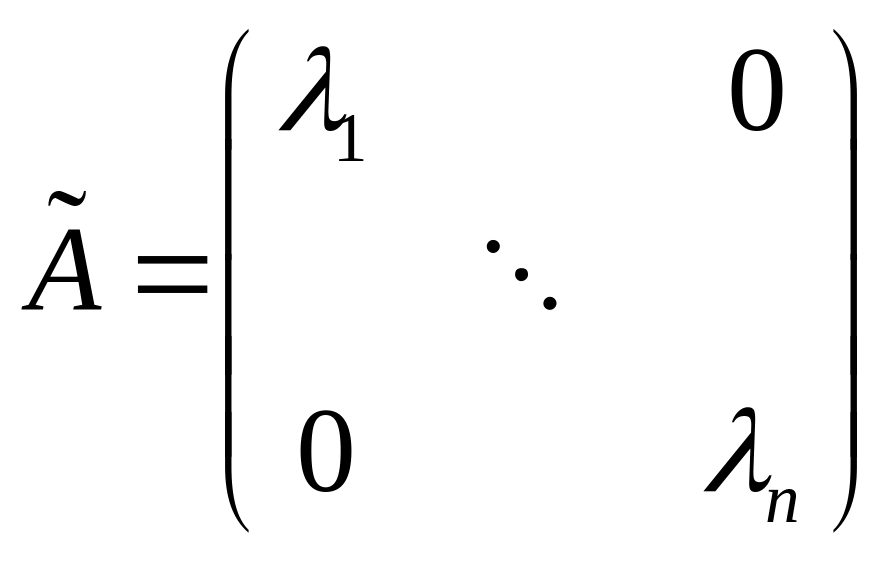де – власні значення лінійного перетворення . За теоремою 1, матриця квадратичної форми збігається з матрицею в цьому базисі. Теорему доведено.

2. Зведення загального рівняння другого порядку з трьома невідомими до канонічного вигляду. Нагадаємо, що в розділі 4 ми зводили загальне рівняння другого порядку з двома невідомими до канонічного вигляду шляхом перетворення прямокутної системи координат – повороту системи координат на певний кут з наступним її паралельним перенесенням. В цьому пункті ми будемо зводити загальне рівняння другого порядку з трьома невідомими до канонічного вигляду, використовуючи отримані результати для квадратичних форм.

Нехай в тривимірному евклідовому просторі задано ортонормований базис , який визначає прямокутну декартову систему координат і розглянемо в цій системі координат загальне рівняння другого порядку з трьома невідомими

(13)

Згідно з теоремою 3 попереднього пункту для квадратичної форми

,

існує ортонормований базис з власних векторів приєднаного лінійного перетворення , в якому вона має канонічний вигляд. Власні значення приєднаного лінійного перетворення знайдемо з характеристичного рівняння

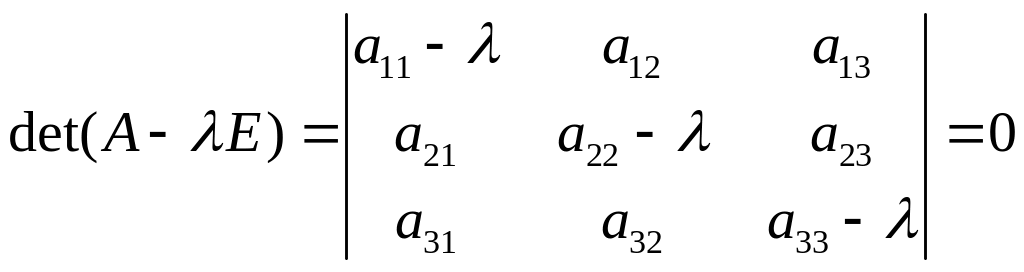
і за власними значеннями знайдемо трійку власних векторів , які утворюють ортонормований базис, що визначає прямокутну систему координат , в якій квадратична форма має канонічний вигляд

.

Очевидно, що при переході від базису до базису за формулою лінійна форма рівняння (13) перетворюється в лінійну ж форму за правилом , , , а вільний член залишається без змін. Звідси, рівняння (13) в системі координат має вигляд

. (14)

Легко побачити, що шляхом виділення повного квадрата відносно кожного з невідомих при квадраті якого відповідне не дорівнює нулеві, рівняння (14) можна звести до одного з таких рівнянь:

Можна показати, що залежно від комбінації знаків коефіцієнтів рівнянь та значення вільного члена кожне з цих рівнянь визначає одну з таких поверхонь другого порядку: 1) еліпсоїд ; 2) уявний еліпсоїд ; 3) однополий гіперболоїд ; 4) двополий гіперболоїд ; 5) конус другого порядку ; 6) уявний конус ; 7) еліптичний параболоїд ; 8) гіперболічний параболоїд ; 9) еліптичний циліндр ; 10) уявний еліптичний циліндр ; 11) пара уявних площин , які перетинаються ; 12) гіперболічний циліндр ; 13) пара площин , які перетинаються ; 14) параболічний циліндр ; 15) пара паралельних площин ; 16) пара уявних паралельних площин ; 17) пара площин , що збіглися.

Приклад. Звести до канонічного вигляду загальне рівняння другого порядку

(15)

і встановити тип поверхні, яка визначається цим рівнянням.

Позначимо через ортонормований базис тривимірного евклідового простору, який визначає прямокутну декартову систему координат в якій задано рівняння (15). Позначимо , , . Для знаходження матриці квадратичної форми її зручно записати так:

.

Звідси,

,

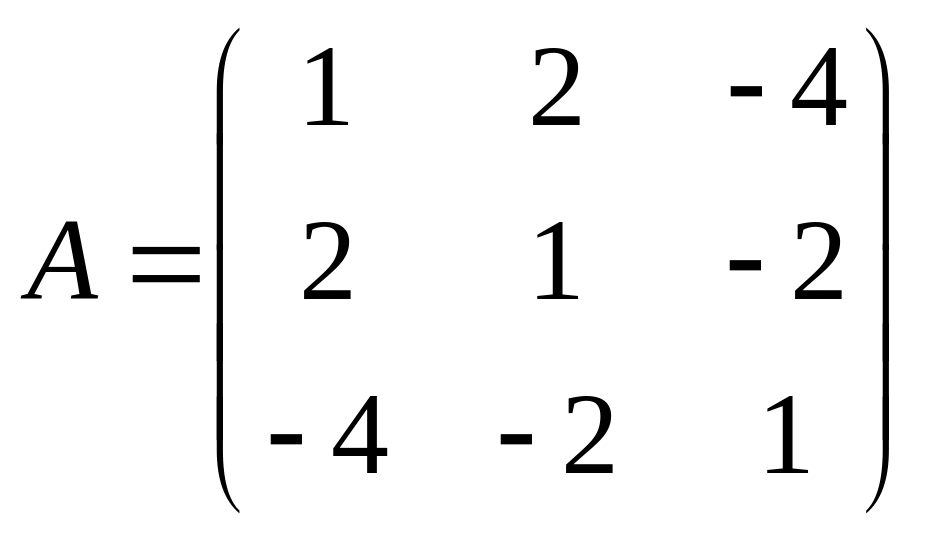яка є одночасно матрицею приєднаного лінійного перетворення в базисі .

Знайдемо власні значення приєднаного лінійного перетворення .

,

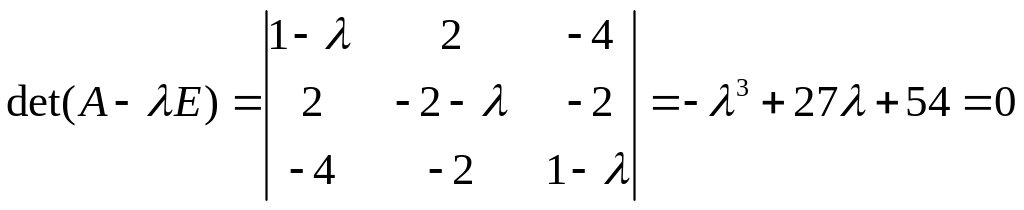звідки , .

Знайдемо власні вектори приєднаного лінійного перетворення .

1). Складаємо лінійну однорідну систему :

,

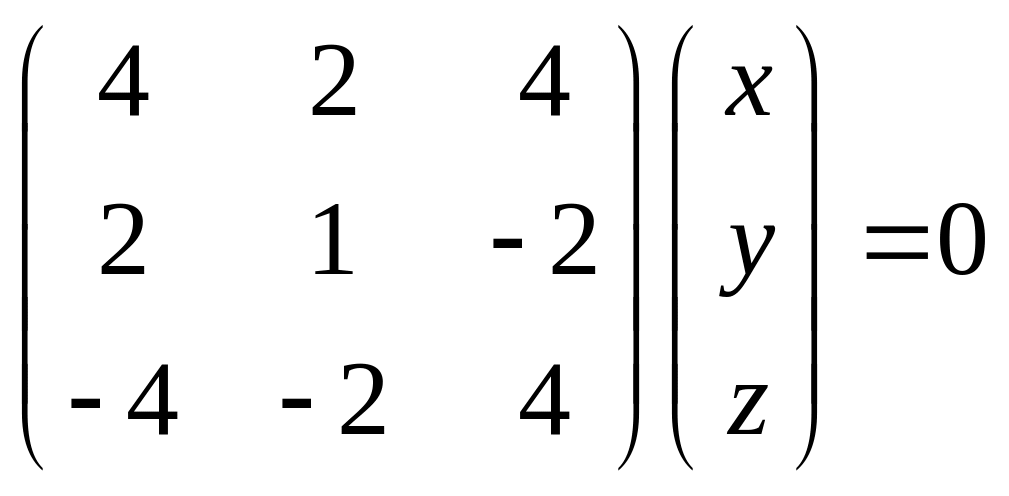тобто

,

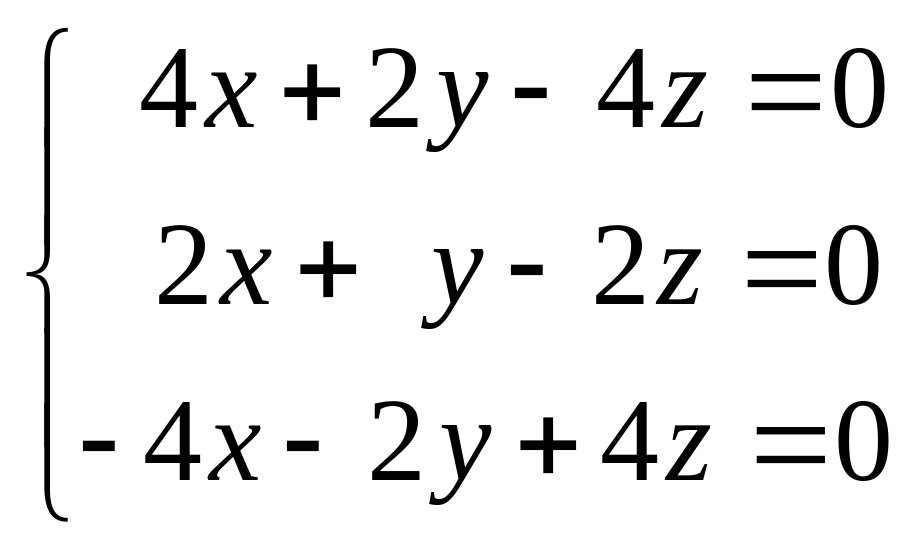максимальна лінійно незалежна підсистема якої складається з одного будь-якого рівняння, наприклад, , звідки знаходимо всі власні вектори – лінійні комбінації пари лінійно незалежних векторів та . Таким чином, власні вектори, що відповідають власним значенням , утворюють двовимірний лінійний підпростір . З допомогою процесу ортогоналізації , , де , знайдемо в підпросторі пару ортогональних векторів , і віднормуємо їх до одиничної довжини:

, .

2) . Складаємо лінійну однорідну систему :

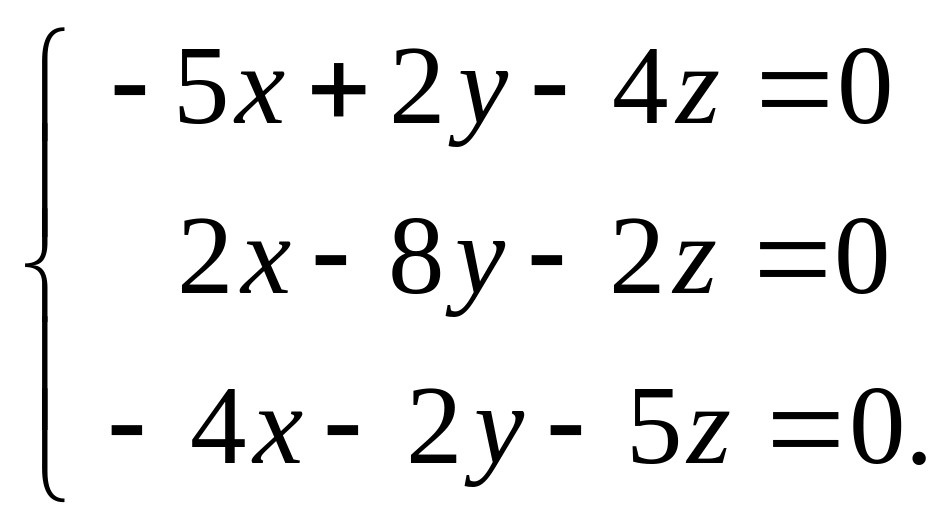
Легко перевірити, що ранг системи дорівнює двом і максимальну лінійно незалежну підсистему складають, наприклад, два останніх рівняння

Загальний розв’язок останньої системи має вигляд: , тобто власному значенню відповідає власний вектор , ортом якого є вектор .

Легко перевірити, а відповідна теорема про базис з власних векторів самоспряженого лінійного перетворення це гарантує, що трійка власних векторів приєднаного лінійного перетворення утворює ортонормований базис тривимірного простору, до того ж

.

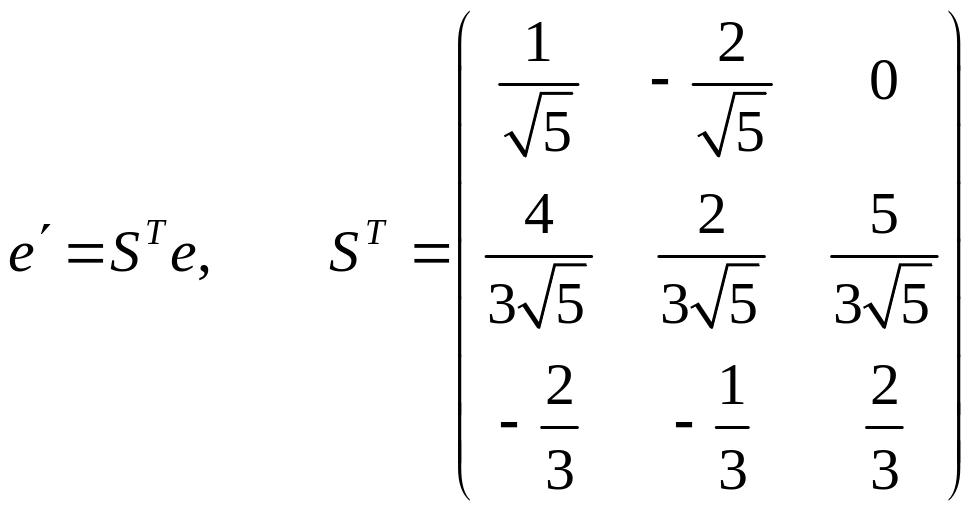В базисі квадратична форма має такий канонічний вигляд:

Щодо лінійної форми , то відомо, що при переході від базису до базису , , стовпчик її коефіцієнтів перетворюється за тим самим правилом , тому

,

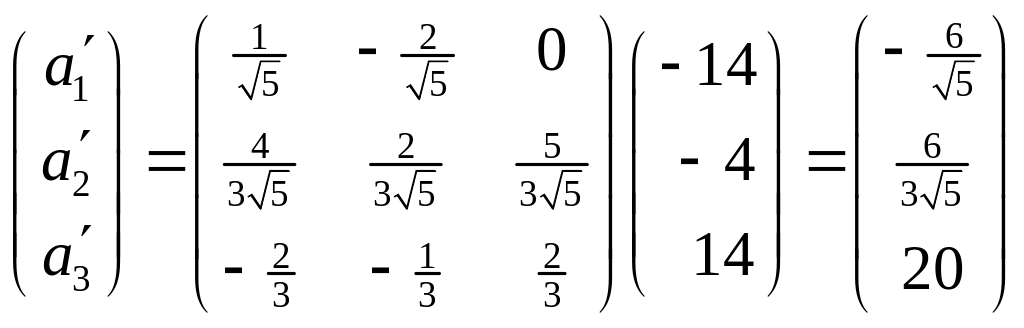тобто .

Таким чином, рівняння (15) в декартовій прямокутній системі координат має вигляд

(16)

В лівій частині цього рівняння перегрупуємо доданки і виділимо повні квадрати:

.

Виконавши паралельне перенесення системи координат

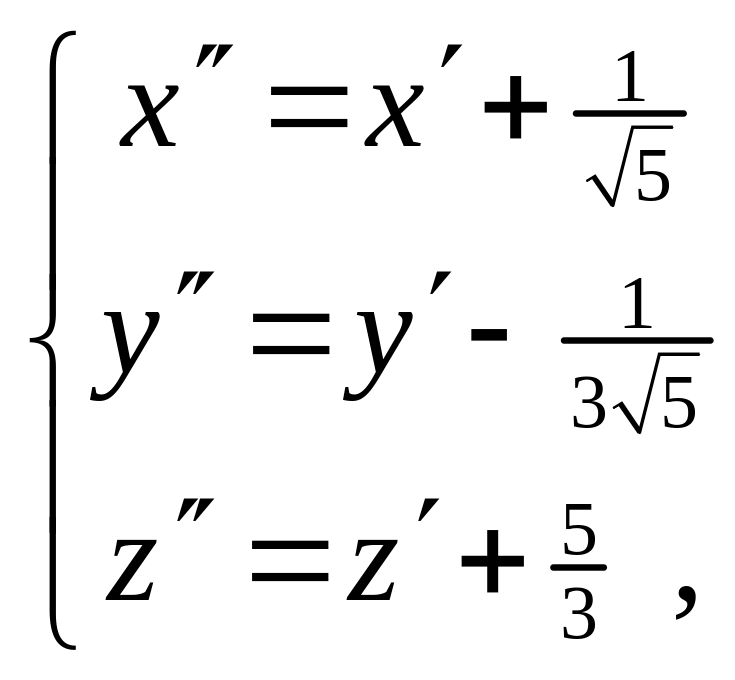
отримаємо канонічне рівняння поверхні (15):

,

або, остаточно,

.

Це канонічне рівняння конуса другого порядку.