3. Контроль дефектов шатуна (трещины) при помощи np-карты (по альтернативному признаку)

Поскольку задано число дефектов для выборки из 15 изделий и n=const, выбирается биномиальная модель и np - контрольная карта.

Исходные данные:

16	2
17	0
18	1
19	2
20	2
21	1
22	2
23	1
24	5
25	0
26	2
27	2
28	1
29	0
30	6
	49

Таблица 3.6.

	np
1	2
2	3
3	0
4	1
5	2
6	3
7	1
8	0
9	4
10	2
11	0
12	1
13	2
14	0
15	1

Предварительная контрольная карта:

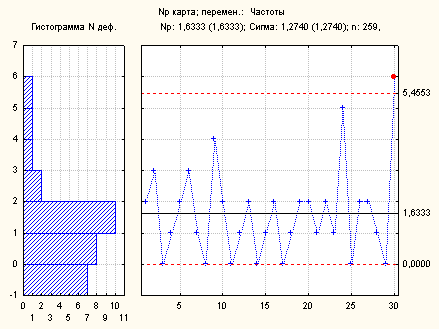
Рис.3.31. Предварительная контрольная np-карта и гистограмма

Примем 30-ю выборку как вышедшую за контрольные пределы вследствие влияния особых причин.

Скорректированная контрольная карта:

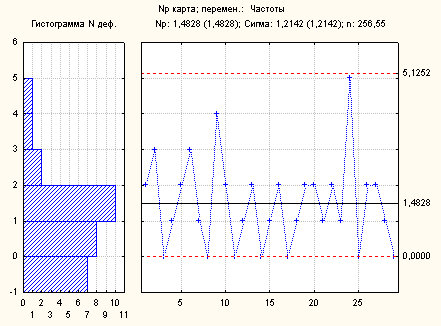
Рис.3.32. Скорректированная контрольная np-карта и гистограмма

Вывод: так как выбросы отсутствуют и распределение точек приблизительно симметрично и случайно, то полученное значение можно принять как стандартное и использовать для дальнейшего контроля.

Проверка на выбросы

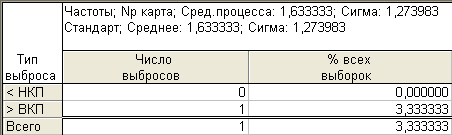
Рис. 3.33. Проверка на выбросы np-карты

1 Выброс за границу ucl до построения скорректированной карты.

Гистограмма

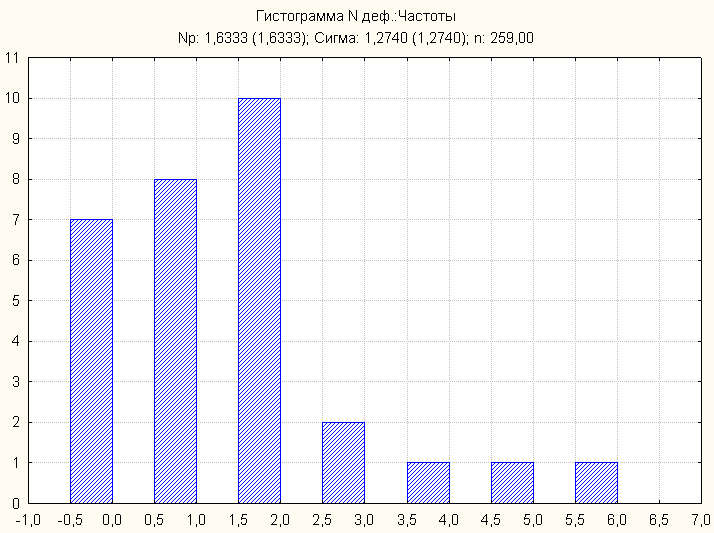
Рис. 3.34. Гистограмма для np-карты

Оперативная характеристика контрольной карты:

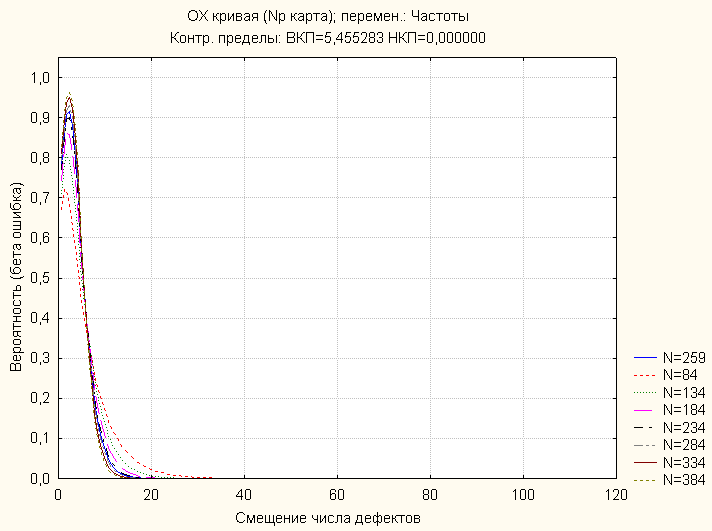
Рис.3.35. Оперативная характеристика np-карты

Проверка нарушения случайности распределения:

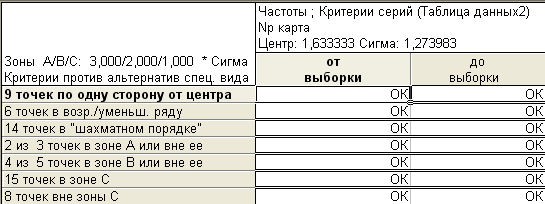
Рис.3.36. Проверка нарушений случайности распределения np-карты

Описание контрольной карты (до корректировки):

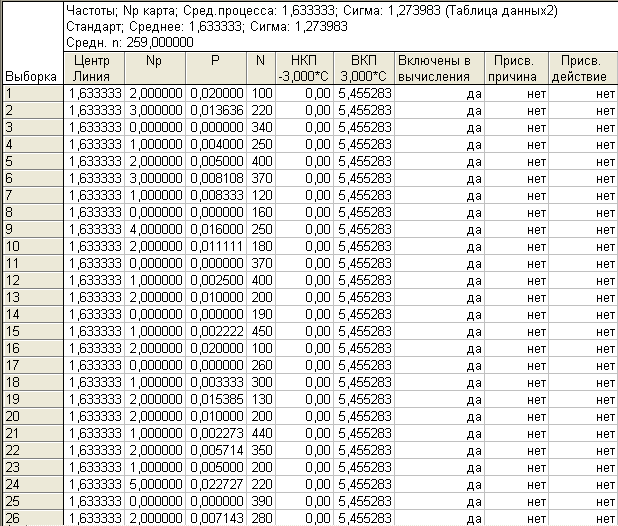
Рис.3.37. Описание контрольной np-карты (до корректировки)

1) Расчет параметров контрольной карты: m=30

;

- средняя доля дефектов

;

;

(принимаем 0)

2) Контрольная карта имеет вид:

Рис.3.38. Контрольная np-карта

Примем 30-ю выборку как вышедшую за контрольные пределы вследствие влияния особых причин.

3) Расчет параметров скорректированной контрольной карты: m=29

;

;

;

(принимаем 0)

4) Контрольная карта со скорректированными значениями и границами имеет вид:

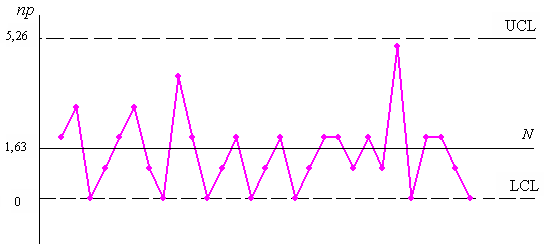
Рис.3.39. Контрольная np-карта со скорректированными значениями

Вывод: так как выбросы отсутствуют и распределение точек приблизительно симметрично и случайно, то полученное значение можно принять как стандартное и использовать для дальнейшего контроля.