Проверка нарушений случайности распределения:

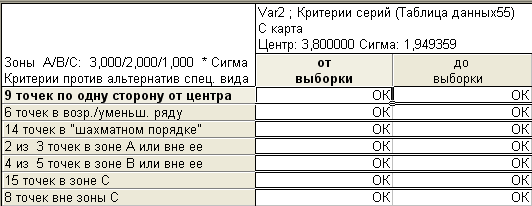
Рис. 3.25. Проверка нарушений случайности распределения для С-карты

Исходные данные для построения Р-карты:

Таблица 3.3.

	№ выборки	Объем выборки n	Число дефектов
1	1	200	2
2	2	320	7
3	3	180	5
4	4	450	9
5	5	290	4
6	6	430	6
7	7	400	2
8	8	390	8
9	9	220	5
10	10	230	4
11	11	350	3
12	12	410	5
13	13	340	6
14	14	170	7
15	15	320	9
16	16	480	1
17	17	230	2
18	18	390	4
19	19	150	3
20	20	200	6

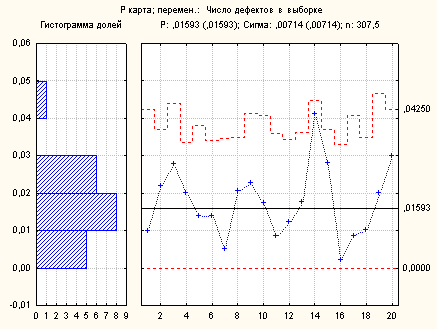
Рис. 3.26. Контрольная Р-карта и гистограмма распределения доли брака

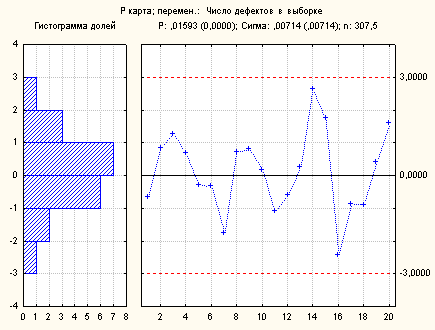
Рис.3.27. Нормализованная контрольная Р-карта и гистограмма

Диаграмма Парето

Таблица 3.4.

	Дефект	Число дефектных изделий
1	Сильный износ	49
2	Трещины	30
3	Ржавчина	11
4	Погнутость головки	20
5	Сколы	19
6	Задиры и царапины на поверхности шатуна	12
7	Шум при работе	14
8	Прочие	5

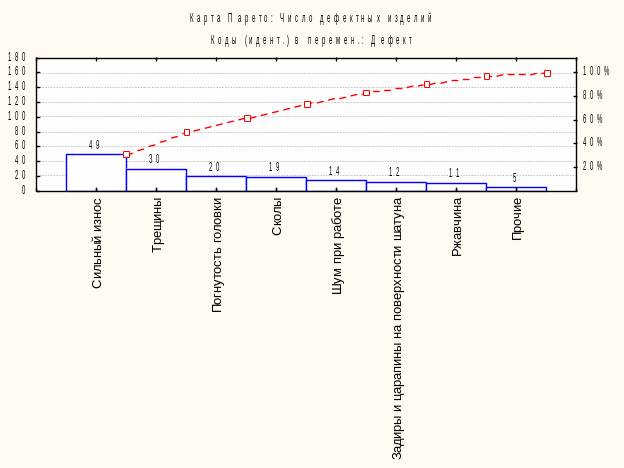
Рис. 3.28. Карта Парето

Вывод: на диаграмме виден эффект Парето, т.к. большинство дефектов находится в первых двух категориях. Основная работа должна быть направлена на устранение дефектов в категориях носящих максимальный вклад: сильный износ, трещины и ржавчина.

Анализ технологического процесса для следующих данных:

Таблица 3.5.

	Х1	Х2	Х3	Х4	Х5	Хср	R
1	32,858	35,458	34,781	31,086	32,827	33,402	4,372
2	33,6	31,168	31,102	34,471	30,319	32,132	4,152
3	36,580	41,552	30,588	34,157	39,092	36,3938	10,964
4	30,726	30,391	33,849	31,266	34,923	32,231	4,532
5	29,889	30,564	32,697	38,748	36,416	33,6628	8,859
6	35,469	39,768	33,922	32,099	34,497	35,151	7,669
						33,829	6,758

1) Расчет среднего арифметического, размаха, общего среднего арифметического и общего размаха:

; ;

;

где , - среднее и размах i-ой (i=1,…k) выборки.

_;

2) Расчет контрольных границ для карты среднего арифметического:

; ,

где А₂ – коэффициент для вычисления контрольных границ (фактор, зависящий от n (n=5))

А₂ =0,577

;

3) Расчет контрольных границ для карты размаха:

; ,

Где D₃, D₄ – коэффициенты для вычисления контрольных границ (факторы, зависящие от n (n=5))

D₃ =0; D₄=2,114

;

4) Контрольные карты имеют следующий вид:

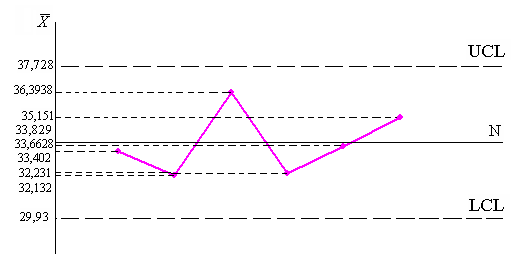
Рис. 3.29. Контрольные карты среднего арифметического

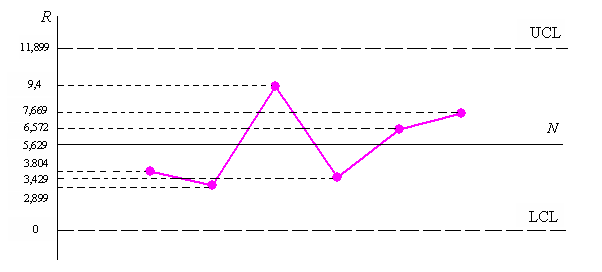
Рис. 3.30. Контрольные карты размаха

Вывод: В построенных картах отсутствует выход результатов за контрольные границы (нет выбросов), периодичность, приближение к центральной линии и линейный тренд, не нарушается случайность распределения точек, т.е. технологический процесс находится в статистически управляемом состоянии. Полученные и принимаем за стандартные значения и используем при последующем контроле.