Алгоритм решения задачи

1. Записать транспортную задачу линейного программирования в канонической форме записи, составить к ней двойственную задачу.

2. Найти начальное решение.

3. Проверить решение на невырожденность.

R[А]=m+n-1 – ранг матрицы

Из размерности ранга матрицы А следует, что число ненулевых решений системы ограничений должно быть m+n-1. В этом случае решение называется невырожденным, а если число ненулевых решений меньше ранга, то такое решение называется вырожденным (вводится значимый нуль ).

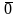4. Вычислить потенциалы и найти оценки.

Потенциалы находят из решения системы (1):

Cij = ui+vj, где

ui, vj - потенциалы

Cij – стоимость перевозки единицы груза

При нахождении потенциалов u и v потенциал u1=0 всегда.

Затем необходимо найти оценки αpq, причем

αpq = Cpq - up – vq

• если все оценки αpq>0, то это признак оптимального решения;

• если имеется оценка αpq=0, то это признак альтернативного оптимума, и выполняется еще один шаг для его нахождения;

• если имеются оценки αpq<0, то минимальная из отрицательных оценок определяет разрешающий элемент.

5. Найти разрешающий элемент.

6. Построить новый план

   1. Начиная с разрешающего элемента, строим замкнутый цикл, вершинами которого будут цифры плана, отличные от нуля.

Цикл может быть представлен следующими фигурами:

2. Помечаем вершины цикла знаками «+» и «−» поочередно, начиная с разрешающего элемента.

3. Находим величину сдвига по циклу ( из тех, где «−»):

Θ= min {xij}, где Z - цикл

xij € Z

4. Строим новый план х1, добавляя или вычитая, в соответствии со знаками, величину Θ к элементам цикла. И переходим на пункт 4.

Замечание 1: если план вырожден, то для нахождения потенциалов выбирается значимый ноль ( ) с наименьшим Cij из оставшихся и так до тех пор, пока не вычислим потенциалы.

Замечание 2: если начальное решение, найденное по методу минимальной стоимости не позволяет найти потенциалы, то применяют метод северо-западного угла для нахождения первоначального решения.