2. Метод потенциалов решения транспортной задачи
2.1 Постановка задачи.
Имеется 3 оптовых склада и 4 магазина
A1, A2, A3 – склады.
a1 = 90, a2 = 70, a3 = 40 – соответственно, запасы на складах.
B1, B2, B3, B4 – магазины.
b1 = 50, b2 = 80, b3 = 20, b4 = 40, - соответственно, потребности магазинов.
|
Bj |
B1 |
B2 |
B3 |
B4 |
|
|||||||||
Ai |
bj ai |
b1=50 |
b2=80 |
b3=20 |
b4=40 |
|
|||||||||
A1 |
a1=90 |
|
x11 |
2 |
|
x12 |
3 |
|
x13 |
4 |
|
x14 |
3 |
||
|
|
|
|
|
|
|
|
||||||||
A2 |
a2=30 |
|
x21 |
5 |
|
x22 |
3 |
|
x23 |
1 |
|
x24 |
2 |
||
|
|
|
|
|
|
|
|
||||||||
A3 |
a3=40 |
|
x31 |
2 |
|
x32 |
1 |
|
x33 |
4 |
|
x34 |
2 |
||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
C=[Сij]mxn
2.2 Построение модели транспортной задачи. Условные разрешимости транспортной задачи.
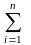ai
=
bj
– условие разрешимости (в противном
случае задача не решается).
Задачи, в которых выполняется это условие, называются «закрытыми транспортными задачами», в противном случае – «открытыми».
Для того чтобы перейти от открытой транспортной задачи к закрытой вводят либо фиктивного поставщика, либо фиктивного потребителя.
Если ai > bj – то вводится фиктивный поставщик.
Если ai < bj – то вводится фиктивный потребитель.
ai = 160
bj = 190
ai bj => вводим фиктивного поставщика
|
Bj |
B1 |
B2 |
B3 |
B4 |
|
|||||||||
Ai |
bj ai |
b1=50 |
b2=80 |
b3=20 |
b4=40 |
|
|||||||||
A1 |
a1=90 |
|
x11 |
2 |
|
x12 |
3 |
|
x13 |
4 |
|
x14 |
3 |
||
|
|
|
|
|
|
|
|
||||||||
A2 |
a2=30 |
|
x21 |
5 |
|
x22 |
3 |
|
x23 |
1 |
|
x24 |
2 |
||
|
|
|
|
|
|
|
|
||||||||
A3 |
a3=40 |
|
x31 |
2 |
|
x32 |
1 |
|
x33 |
4 |
|
x34 |
2 |
||
|
|
|
|
|
|
|
|
||||||||
A4 |
a4=30 |
|
x41 |
0 |
|
x42 |
0 |
|
x43 |
0 |
|
x44 |
0 |
||
|
|
|
|
|
|
|
|
||||||||
min [fo(x) = 2x11 + 3x12 + 4x13 + 3x14 + 5x21 + 3x22 + x23 +2x24 + 2x31 + x32 + 4x33 + 2x34]
XЄR
R = X |
U1 |
X11+X12+X13+X14 |
= 90 |
|
U2 |
X21+X22+X23+X24 |
= 30 |
||
U3 |
X31+X32+X33+X34 |
= 40 |
||
U4 |
X41+X42+X43+X44 |
= 30 |
||
V1 |
X11 +X21 +X31 +X41 |
= 50 |
||
V2 |
X12 +X22 +X32 +X42 |
= 80 |
||
V3 |
X13 +X23 +X33 +X43 |
= 20 |
||
V4 |
X14 +X24 +X34 +X44 |
= 40 |
А = |
|
1111 0000 0000 0000 |
0000 1111 0000 0000 |
0000 0000 1111 0000 |
0000 0000 0000 1111 |
|
rank A = (m+n)-1
rank A = 7
Построим двойственную задачу
Введем дополнительные переменные
max [go(U,V) = 90U1+30U2+40U3+30U4+50V1+80V2+20V3+40V4]
U,VЄQ
Q= |
|
U1+V1≤2 |
|
|
U1+V2≤3 |
||
|
… |
||
|
Ui+Vj≤Cij |
||
|
i=1,2,3,4 |
||
|
j=1,2,3,4 |
||
|
Ui ≥ ≤ 0 |
||
|
Vj ≥ ≤ 0 |
Модель транспортной задачи в общем виде:
min
[fo(x)=
CijXij]
XЄR
R = x |
Xij=ai, i=1, 2, …, m |
|
|
Xij=bj, j=1, 2, …, n |
|
||
X ≥ 0 |
|
Модель транспортной задачи в общем виде. Прямая задача.
max [go(U,V)
=
aiUi
+
bjVj]
U,VЄQ
Q = U,V |
Ui + Vj ≤ Сij |
|
|
U ≥≤ 0 |
|
||
V ≥≤ 0 |
|
Строить модель можно только для закрытой задачи линейного программирования.