Лабораторная работа №3. Генерация псевдослучайных чисел.

Генерация псевдослучайных чисел. Исследование качества полученной последовательности в зависимости от входных параметров. Проверка соответствия равномерному закону распределения. Использование метода Монте-Карло для вычисления определенного интеграла

Задания

Создать программу для генерирования случайных чисел на основе конгруэнтного алгоритма Лемера. Сгенерировать последовательность из 100 чисел. Провести эксперименты на исследование качества полученной последовательности. Проверить равномерность распределения на основе анализа гистограмм.

Задание по вариантам

Сформировать по 100 чисел равными методами (по варианту), проверить каждую последовательность на равномерность распределения.

Провести эксперименты, найти случаи, когда начинается повторении серии псевдослучайных чисел (взять соответствующие входные данные).

Провести эксперимент , вести протокол результатов и отслеживать поведение результата. Сделать выводы. Оформить отчет и ответить на вопросы.

Указания

• Выполнить задание

• Создать отчет и ответить на вопросы

• Показать преподавателю

Вопросы к лабораторной работе

1. Какие недостатки имеют алгоритмы Лемера?

2. Как формируются элементы последовательности псевдослучайных чисел при использовании стандартной функции в разных языках программирования?

3. Зачем нужно при шифровании генерировать псевдослучайные последовательности с максимальным периодом?

4. В чем суть конгруэнтных генераторов?

5. Опишите построение последовательности на основе рекурсивных последовательностей

6. Как применяют псевдослучайные последовательностей?

7. Каковы недостатки любой псевдослучайной последовательности?

Приложение-файлы в папке

Краткая теория

1. Необходимость генерации случайных чисел

Имитационное моделирование позволяет воспроизводить процесс сложные процессы и явления.

Основной для создания компьютерной имитационной модели является формирование последовательностей значений случайных величин.

2. Компьютерная генерация равномерно распределенных случайных чисел

Самостоятельное программирование генератора равномерно распределенных случайных чисел:

1. Самый первый алгоритм - метод срединных квадратов или алгоритм фон Неймана. Берется произвольное число  ₀ , состоящее из 2n двоичных цифр. Величина  ₀  возводится в квадрат, который состоит уже из 4n цифр. Далее выбирается  ₁  из 2n средних двоичных цифр квадрата, и в дальнейшем процесс повторяется в той же последовательности.

2. Самый легкий в реализации-конгруэнтный алгоритм Лемера (много видов). Числа а и b конгруэнтны по модулю m , если их разность кратна числу m. Отношение сравнения (конгруэнтности) записывают так a:b(mod m). Эта запись означает, что разность a  b делится на m без остатка или, другими словами, числа a и b дают одинаковый остаток при делении на m. Например, 1364 = 4(mod 10), 1262 = 162(mod 100).

3. `Реализации конгруэнтного алгоритма генерации случайных чисел:

А)r _i+1 = a r_i (mod m)  мультипликативный алгоритм,

где a , m -неотрицательные целые числа,

r_i, r_i+1  очередное и последующее случайное число,

В)r_i+1 = ar_i + c (mod m)  смешанный алгоритм,

С)r_i+1 = r_i + r_i-1 (mod m)  аддитивный алгоритм.

Известны и другие методы: метод Фибоначчи с запаздываниями, алгоритм Блюма, Блюма и Шуба, Вихрь Мерсенна и др.

Рекомендации по программированию

По формулам составить процедуру (функцию) генерации псевдо случайных чисел.

При использовании мультипликативного алгоритма для получения последующего случайного числа r_i+1 нужно взять последнее случайное число r_i умножить его на a  и взять модуль полученного числа по m, т.е. разделить на m и принять за остаток r_i+1.

Выбор a, m, r₀ (первого числа) производится из условия обеспечения минимальной корреляции между генерируемыми числами и максимального периода повторения последовательности цифр. Обычно m=2^b, где b  число двоичных цифр в машинном слове.

Интересно проверить полученную последовательность на соответствие равномерному закону распределения.

Использование встроенного в язык программирования генератора псевдослучайно распределенных чисел

Стандартная функция (обычно RND) выдает случайное число, равномерно распределенное в интервале от 0 до 1. Используя линейное преобразование можно получать случайные числа в разных интервалах.

Для обеспечения генерирования, не повторяющихся последовательностей, используется RANDOMIZE.

Лабораторная работа №4

Формирование последовательностей псевдослучайных чисел заданного закона распределения

Задание сгенерировать псевдослучайную последовательность равномерно распределенных чисел (100 чисел). Построить гистограмму (не менее 5 интервалов). На основе полученной последовательности сгенерировать последовательность заданного закона распределения. Построить гистограмму. Проверить гипотезу о соответствии показательному распределению и распределению Пуссона (уровень значимости 0,05) . Критерий Пирсона

См. пример по показательному распределению в учебнике Гмурмана-файл

Пример проверки о соответствие распределению Пуссона

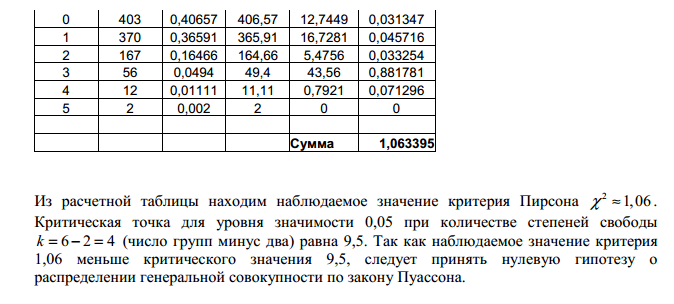
Контрольные вопросы

1. Опишите процедуру генерации псевдослучайной последовательности по заданному закону распределению

2. Как на основе полученной последовательности получить, например, вероятности попадания на участок [0,1]?

Краткая теория

Генерация значений случайных величин, распределенных

по заданным законам распределения

Случайные величины имеют закон распределения. При равномерном законе распределения-все очевидно, имеются известные алгоритмы и встроенная функция.

Генерация значений случайных величин, подчиняющихся другим законам, основана на базовой модели генерации в ЭВМ равномерно распределенных случайных чисел и последующего преобразования этих чисел. Известны несколько методов преобразования (тема реферата для желающих-см. приложение). Самый распространенный метод преобразования — метод обратной функции.

Основы метода обратной функции

Случайная величина Х описывается интегральной F(x) и дифференциальной f(x) функциями распределения. Зная одну из них, можно описать поведение случайной величины. Эти функции связаны между собой

f(x) = F’(x).

Интегральная функция представляет собой вероятность того, что какое-то взятое фиксированное значение Х будет меньше текущего значения x F(x) = Р (Х<х). Очевидно, что с повышением текущего значения Х эта вероятность будет стремиться к 1. Функция F(х) является монотонно возрастающей функцией. Всегда при x₂ > x₁ F(x₂) > F(x₁).

Соответственно, при

P[F(x₁) < F(x₂)] = Р(х₁ < х₂),

Примем, что случайная величина r = F(x).

Найдем распределение этой величины F_r (r).

На основании приведенных выражений

F_r (r) = P(R < r) = P[F(X) < F(x)] = F (X < х) = F(x) = r

R = F_r (r)-F (x). (2.1)

Согласно выражению (2.1), вероятность попадания случайной величины в интервал 0 – r равна длине этого интервала, и это есть признак того, что данное распределение равномерное.

В результате получаем алгоритм формирования непрерывной случайной величины Х по заданному закону распределения. Поскольку r_i = F ( x_i ), то необходимо выполнить преобразование

X_i = F^-1 ( r_i ), (2.2)

где r_i — равномерно распределенное случайное число;

F^-1 — функция, обратная по отношению к распределению случайной величины X.

На основании выражения (2.2) можно моделировать случайные числа с заданным законом распределения.