2.2 Емкостный фильтр

Емкостный фильтр Ф в простейшем виде состоит из конденсатора , подключенного параллельно сопротивлению нагрузки (рис . 9) . Источ − ником питания по отношению к фильтру и нагрузке является выпря − митель В . На эквивалентной схеме (рис . 9.,б) напряжение на емкости (на сопротивлении нагрузки) представлено суммой переменной U_~ и постоянной U₀ составляющих . Принцип действия емкостного фильтра изложен в п. 1.5 .

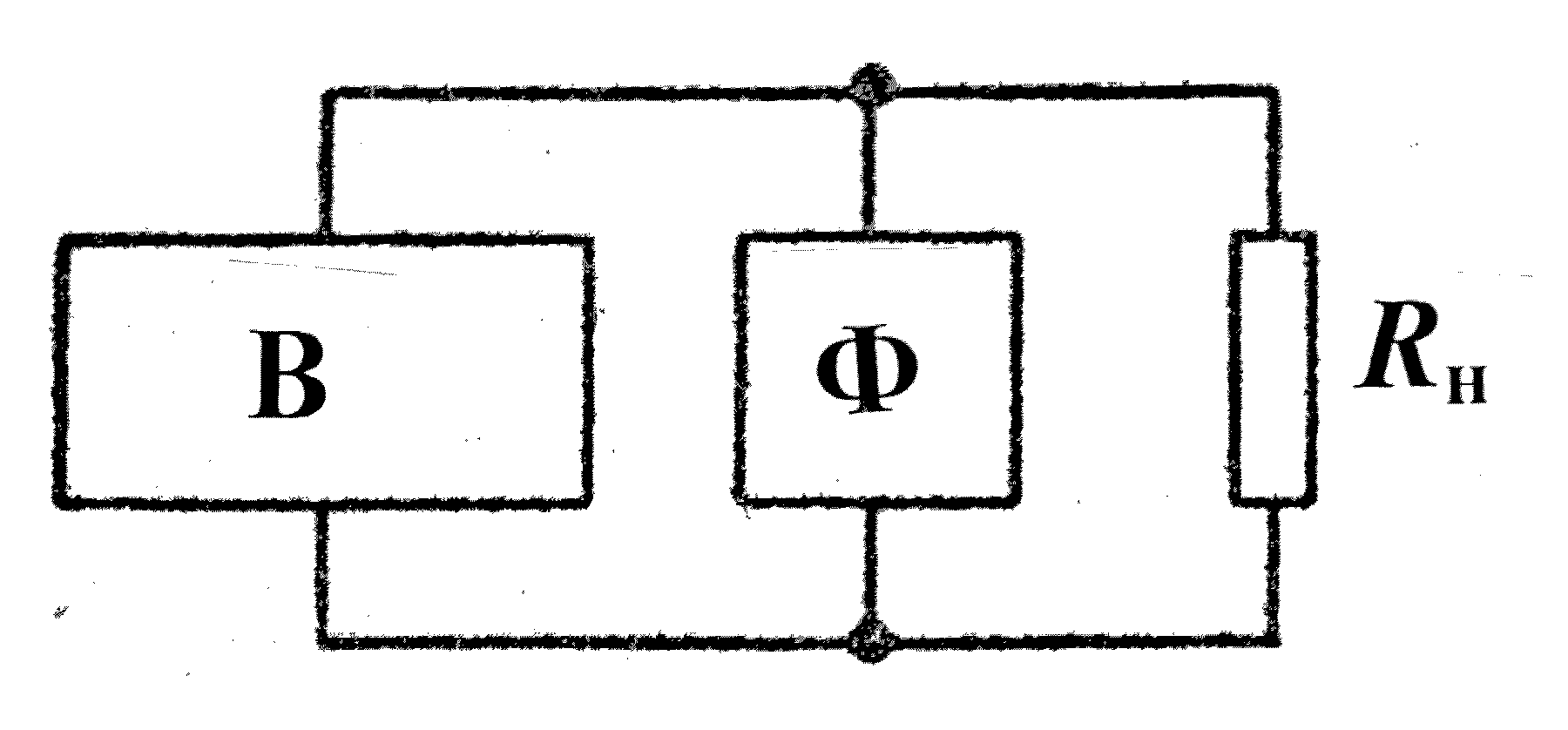
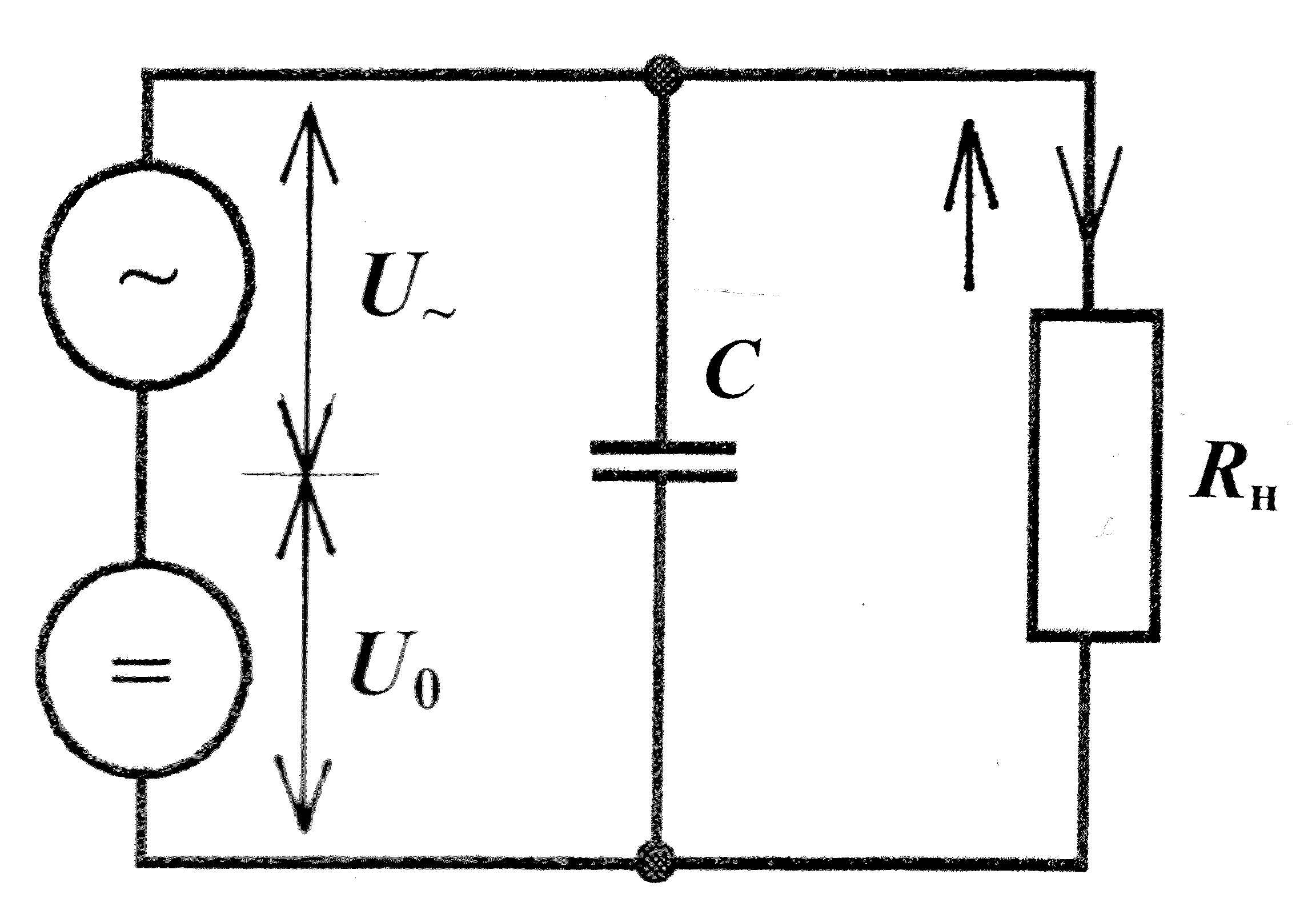
а б

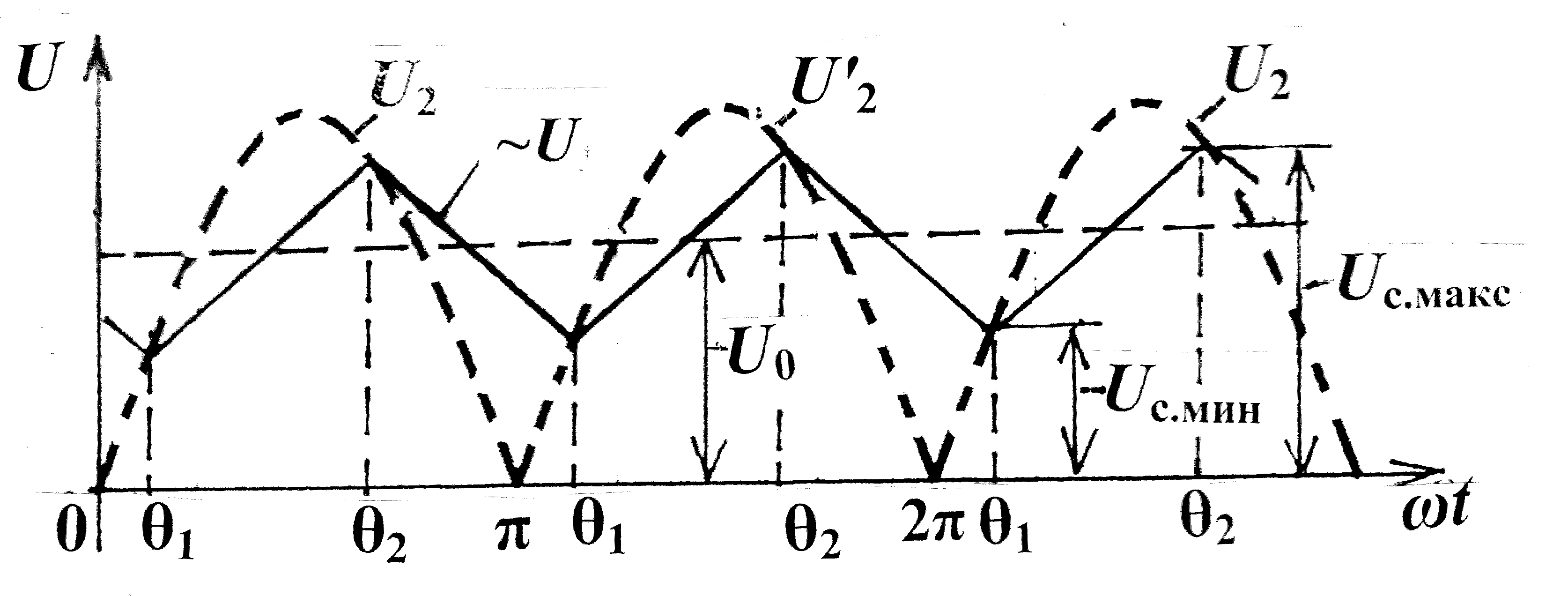
в

Рис. 9

Соотношения для расчета С – фильтра , когда источником питания яв – ляется многофазный выпрямитель , получаются из следующих рассужде – ний . Приближенно можно считать . что процесс заряда в интервале фазовых углов θ₁…θ₂ и разряда в интервале θ₂…θ₁ происходят по ли − нейному закону (см. график изменения U_c = U₀ на рис.9 в) . Линейному закону изменения U_c соответствует заряд (разряд) постоянным током . В интервале разряда ток i_c = i₀ , а учитывая , что количество электричества , запасаемого конденсатором при заряде и расходуемого при разряде , в установившемся режиме одинаково , можно принять , что конденсатор заряжается постоянным током I_c ≈ I₀ .

Изменение напряжения на конденсаторе при его разряде определяется из соотношения

,

где C – емкость конденсатора фильтра ;

f = 1/T – частота тока питающей сети ;

m – число фаз выпрямления , причем ток разряда принят равным току нагрузки I₀ .

Изменение напряжение на конденсаторе ΔU_c при разряде (заряде) равно удвоенной амплитуде пульсации U_m~ (ΔU_c = 2U_m~) . Отсюда сле − дует , что коэффициент пульсации напряжения на нагрузке R_н , включен − ной параллельно конденсатору С , можно представить в виде

.

Если задано значение коэффициента пульсации S ^′₀ , То необходимая величина емкости конденсатора

.

Допущения , сделанные при выводе формул для расчета фильтра , лишь незначительно отражаются на его точности . Как показывают опытные данные величина емкости , вычисленная по полученной фор − муле несколько меньше действительно необходимой для получения заданного коэффициента пульсации .

Что следует учитывать , применяя емкостный фильтр ?

1 . Энергия , запасаемая в электрическом поле конденсатора пропор − циональна квадрату напряжения U_c , поэтому емкостный фильтр целесо − образно использовать , когда нагрузка − высоковольтная и высокоомная (с относительно малым потреблением тока) .

2 . Чтобы получить высокий коэффициент сглаживания S′₀ необходим конденсатор большой емкости , а это приводит к росту амплитуды им − пульсов тока заряда , протекающего через диоды .

3 . Емкостный фильтр перегружает источник питания (выпрямитель) и вторичную обмотку трансформатора импульсным током . В результате растут потери , возникает потребность в использовании импульсных , более дорогих диодов .

2.3 Индуктивный фильтр

Индуктивный фильтр представляет собой обмотку (катушку) , намо − танную медным проводом на изолирующем каркасе с ферромагнитным сердечником . В технике такие устройства называют также дросселями . Параметрами дросселя являются номинальный ток I₀ , индуктивность L и активное сопротивление обмотки R_d . Индуктивный фильтр Ф (дроссель) включается между источником выпрямленного напряжения В и сопро − тивлением нагрузки R_н как это показано на рис . 10 , а .

Если пренебречь выходным сопротивлением выпрямителя , как ис − точника питания (сопротивлением диодов , выходным сопротивлением трансформатора) и представить пульсирующее напряжение U_в в виде суммы U₀ и U_~ , то можно воспользоваться схемой замещения (рис.10 ,б).

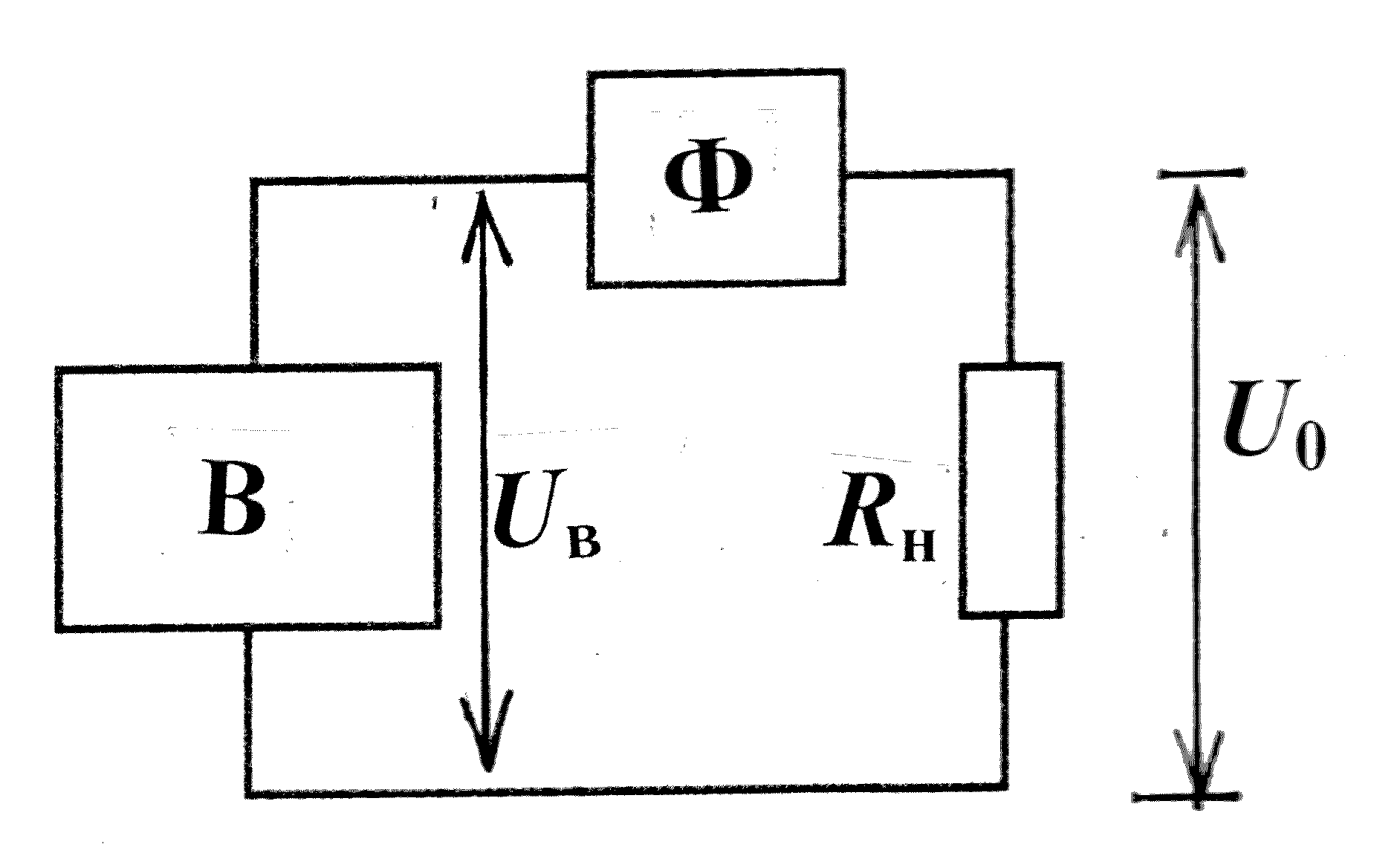
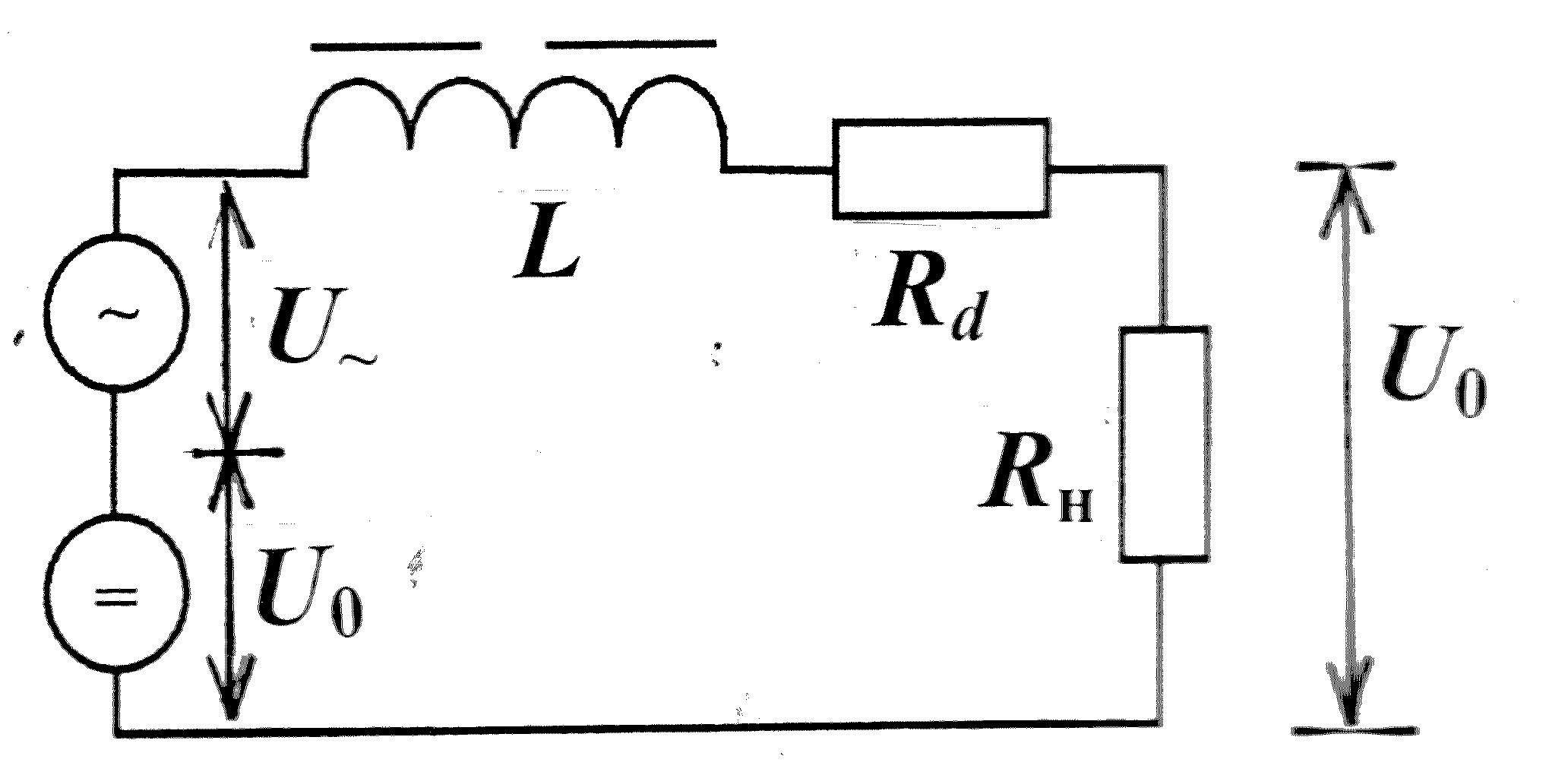
а б

Рис. 10

При отсутствии фильтра составляющими напряжения и тока в цепи нагрузки будут U₀ , U_~ ; I₀ =U₀/R_н , I_~ = U_~/R_н в этом случае коэффици − ент пульсации

.

При наличии индуктивного фильтра составляющими напряжения и тока в цепи нагрузки будут

U′₀ = I′₀∙R_н , U′_~ = I′_~R_н ;

,

а коэффициент пульсации по напряжению

.

При заданной схеме выпрямления значение S0 известно , а величину S′0 определяют в зависимости от вида нагрузки . Значит практически надо найти индуктивность дросселя фильтра по заданному значению коэффициента сглаживания

,

отсюда

L = .

Величиной R_d можно задаться ; полагая R_d = (0,05…0,01) при мощнос − ти выпрямителя P₀ ≈ 0,5…10кВт . Значение R_d уточняется в процессе расчета . Если принять , что R_н >> R_d , g >> 1 , то расчет индуктивности фильтра упростится

.

Сглаживающее (фильтрующее) действие индуктивного фильтра определяется величиной запасаемой энергии

,

следовательно применение индуктивных фильтров целесообразно в вы − прямительных устройствах с большим потреблением тока . К недостат − кам индуктивных фильтров относятся следующие :

а) сглаживающее действие L – фильтра непостоянно , т. к. с изменением потребляемого нагрузкой тока I₀ индуктивность меняется ;

б) при обрыве цепи нагрузки или резком её уменьшении , возможно перенапряжение за счет э.д.с. самоиндукции дросселя . Для защиты от перенапряжения в мощных установках дроссель шунтируется разрядни − ком , который срабатывает при появлении перенапряжении .

2.4 Г – образный LC – фильтр

Фильтр начинается с дросселя , его схема замещения представлена на рис . 11 . В цепи фильтра и нагрузки действуют переменная U_~ и пос – тоянная U₀ составляющие напряжения . Из схемы замещения следуют очевидные соотношений

U_~ = I_~∙Z , U′_~ = I_~∙Z , U′_~ = U_~(Z′/Z) и g = Z′/Z .

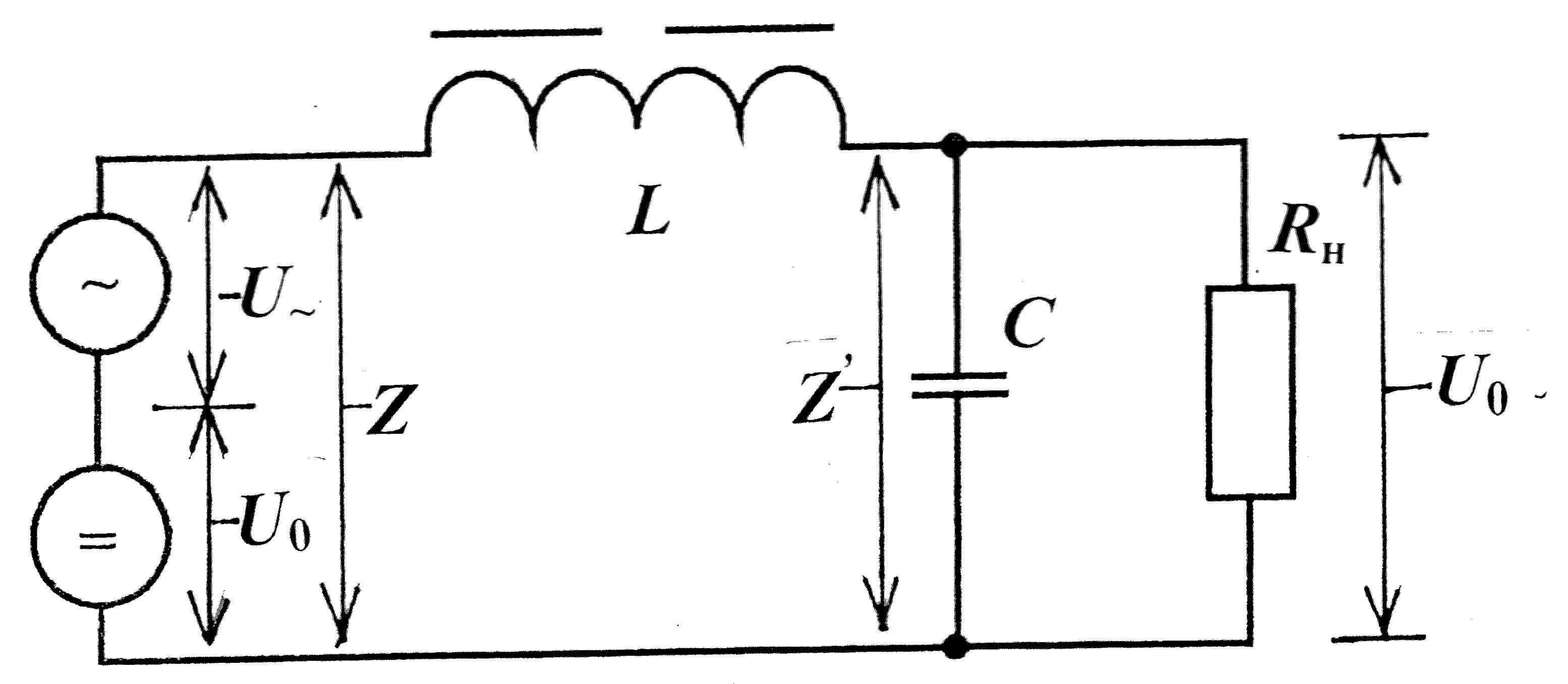
Рис. 11

Обычно активное сопротивление обмоток трансформатора , дросселя и диодов много меньше R_н и для простоты ими пренебрегаем , тогда

Z′ = R_н||jX_c = ; Z = .

Коэффициент сглаживания пульсации определяется как отношение модулей Z и Z′

.

Если индуктивность дросселя выразить в Гн , а емкость конденсатора в мкФ , то при частоте питающей сети f_c = 50Гц

LC = ,

при f_c = 400Гц

.

Здесь g – заданный коэффициент сглаживания . LC – конструктивный параметр фильтра , который рекомендуется выбирать , так , чтобы выпол – нялось условие mω_cL > (mω_cC)⁻¹ , т. е. , чтобы реакция фильтра в целом была индуктивной . Необходимо также обеспечить такое соотношение X_c X_L , чтобы не возникли резонансные процессы на частоте пульсации . Для этого собственная частота фильтра и частота пульсации напряжения должны резко отличаться друг от друга . В применении к многофазным выпрямителям следует реализовать неравенство

,

где ω_ф – собственная частота фильтра .

2.5 П – образный LC – фильтр

П – образный LC – фильтр можно изобразить как показано на рис . 12 в виде двухзвенного фильтра , состоящего из двух : ёмкостного С и Г – образного LC . Сглаживающее действие П – образного фильтра упрощенно представляется как совместное действие обоих звеньев . Коэффициент сглаживания П – образного фильтра g_п =g_сg_LC , где g_п и g_LC – коэффициенты сглаживания составляющих звеньев .

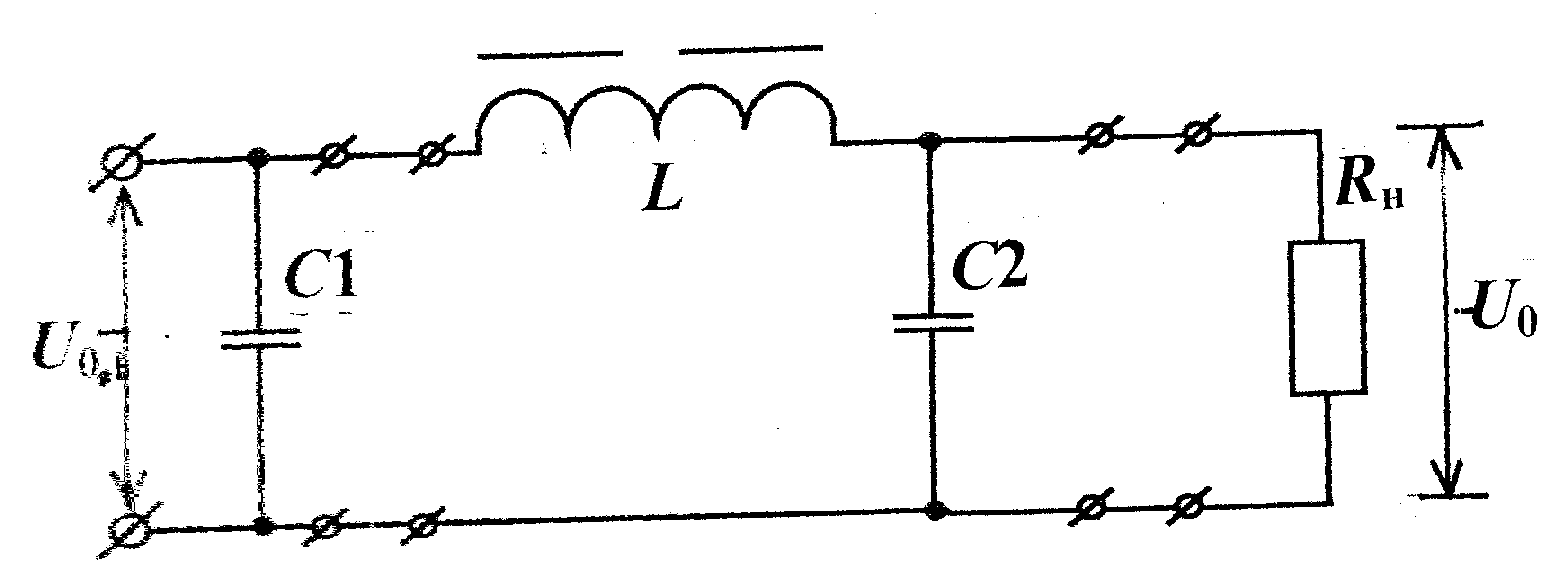
Рис. 12

Расчет П – образного фильтра осуществляется в следующем порядке :

1 . По формуле

определяется величина ёмкости С₁ , которую надо округлить до ближай − шего значения типовых номиналов . Практически рекомендуется для расчета C₁ выбирать значение S′_0.c в пределах 0,2…0,5 .

2 . Определяем требуемый коэффициент сглаживания Г – образного фильтра по допустимому значению коэффициента пульсации напряжения на нагрузке g_г = S_o.г/S′₀ ,

где S_0.г – коэффициент пульсации напряжения на входе Г – образного фильтра , при этом S_0.г = S′_0.1 ; S′₀ – коэффициент пульсации на выходе П – образного фильтра .

3 . По полученному значению g_г и ранее приведенным расчетным соотношениям определяем величину L , приняв C₁ = C₂ .

Примечание . Чтобы определить опытным путем коэффициент сгла − живания пульсации g необходимо провести следующие измерения .

При заданном токе нагрузки I₀ зафиксировать и записать напряжения U_0.1 и U_1~ на входе фильтра ; измерить и записать U₀ и U_~ на выходе фильтра ; рассчитать коэффициенты пульсации на входе S₀ и на выходе S′₀ фильтра ; рассчитать коэффициент сглаживания пульсации g = S₀/S′₀ .

При расчете g емкостного фильтра S₀ − это коэффициент пульсации напряжения до подключения емкостного фильтра , S′₀ – после подключе − ния конденсатора .