1.6 . Работы выпрямителя на активно-индуктивную нагрузку

На рис . 6 приведена схема однофазного однополупериодного выпря − миттеля , в цепь нагрузки которого включен сглаживающий дроссель с индуктивностью L . Как работает схема ?

В начале положительного полупериода U₂ диод V смещается прямо , появляется и увеличивается ток i₂ = i₀ , под действием возрастающего напряжения , при этом форма тока будет отличаться от формы U₂ . От − личие обусловлено противо-э.д.с. , наводимой на концах обмотки дрос − селя , которая противодействует как быстрому росту , так и уменьшению тока i₂ = i₀ . Противо-э.д.с. , наводимая в обмотке дросселя – это прояв − ление процессов накопления энергии в магнитном поле его сердечника при росте тока и расходования запасенной энергии при уменьшении тока .

Когда напряжение U₂ уменьшается в своем , положительном полупе − риоде , ток тоже начинает снижаться , противо-э.д.с. меняет знак (знаки в скобках на концах обмотки дросселя , рис. 6 , а) и поддерживает диод V открытым некоторое время даже в отрицательном полупериоде , проти − водействуя напряжению U₂ . Таким образом , выключение диода прои − зойдет при ωt = β > π . Интервал проводимости диода λ при наличии индуктивности в цепи нагрузки будет больше полупериода .

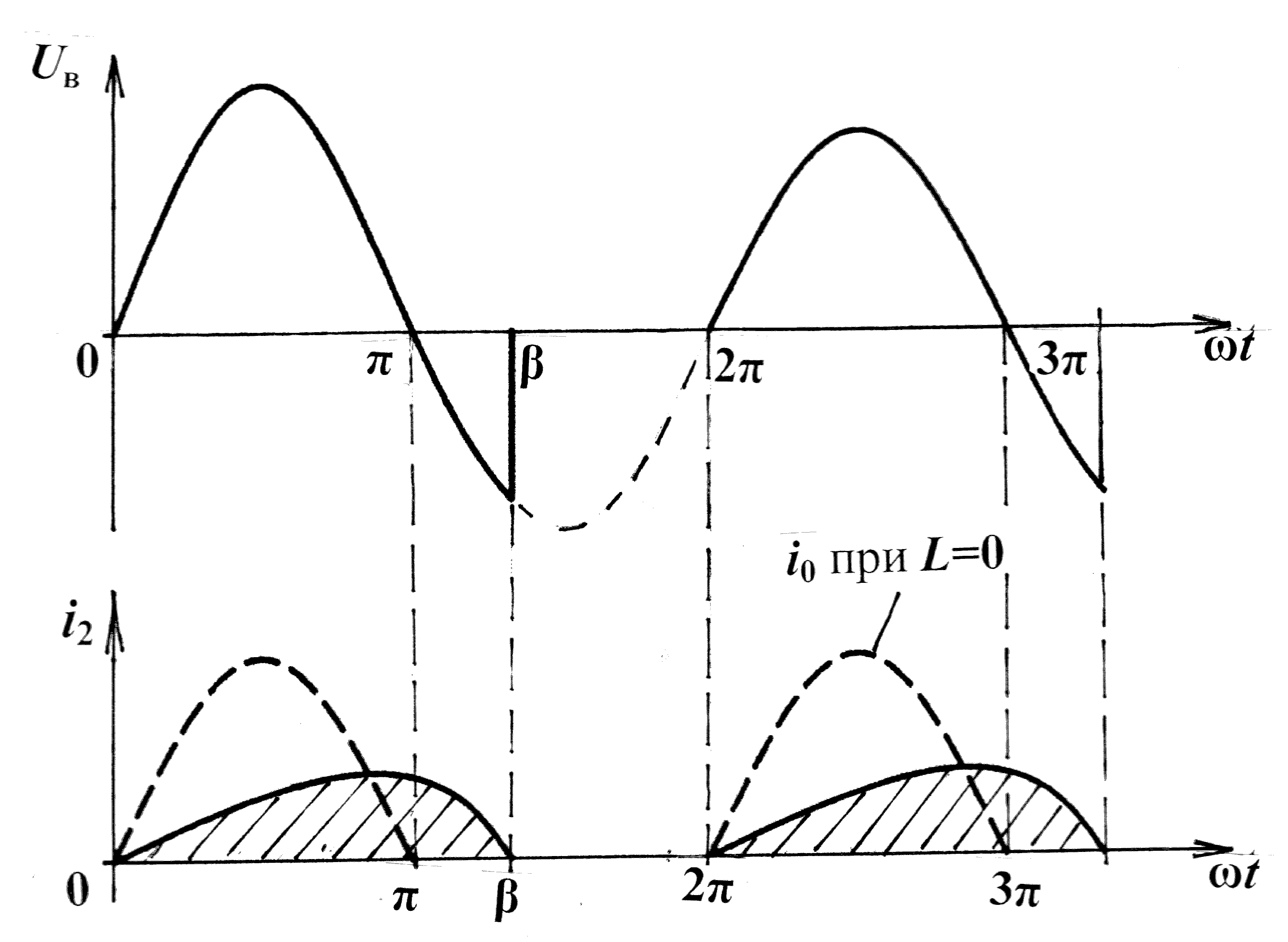
а б

Рис. 6

Форма выпрямленного напряжения U_в , т.е. на RL – нагрузке пред − ставлена на рис. 6 , б . Форма же выпрямленного тока i₂ = i₀ (напряжения i₂R_н = i₀R_н) отличается от формы напряжения U_в. .

Из курса электротехники известно , что энергия , запасаемая в маг − нитном поле сердечника дросселя определяется соотношением

.

Очевидно , чем больше индуктивность L сглаживающего дросселя или , чем больше постоянная времени цепи нагрузки τ = L/R_н , тем больше энергия , запасаемая в дросселе , больше интервал проводимости диода λ и угол β , где λ = π + β .

Выпрямленное напряжение U_в с учетом λ = π + β равно

.

При увеличении L (τ) и соответственно β выпрямленное напряжение и ток нагрузки стремятся к 0 , отсюда следует вывод : однопульсные вы − прямители в качестве источников питания не эффективны .

В схемах многофазных выпрямителей каждый диод подключает цепь нагрузки к соответствующей фазной обмотке трансформатора в своем рабочем полупериоде . Работа многофазного выпрямителя на RL – наг − рузку имеет особенности . Как пример , рассмотрим процессы в двух − фазном однополупериодном выпрямителе (рис. 7) . Как и ранее полагаем , что диоды V1 , V2 обладают свойствами идеальных ключей , а индук − тивности рассеяния и активные сопротивления обмоток трансформатора равны нулю . Этому случаю соответствуют графики напряжения и тока , представленные на рис . 7 , б .

В многофазных схемах уже при небольшой индуктивности дросселя ток нагрузки может стать неразрывным , так как к концу интервала проводимости диода не успевает снизится до нуля . При этом , если в интервале 0…π в проводящем состоянии находился диод V1 , то в мо −

а б

Рис. 7

мент ωt = π , должно произойти мгновенное выключение V1 и включение V2 . Соответственно ток i₀ должен перейти из V1 в V2 . Таким образом , в идеале соблюдается условие неразрывности тока в цепи с индуктив − ностью

На рис .7 , б приведены графики тока через диоды выпрямителя (i_v1 , i_v2) и напряжения нагрузки U₀ при значениях τ_н = 0 ; 0,5 ; 10 . Из гра − фиков видно , что с ростом индуктивной составляющей нагрузки вып − рямителя форма тока через диоды приближается к прямоугольной , а пульсация тока нагрузки становится малой .

Теперь рассмотрим работу выпрямителя с учетом сопротивления по − терь . На рис . 8 , а каждая вторичная фазная обмотка представлена ис − точником переменного напряжения U₂ , U′₂ с внутренним сопротивле − нием в виде R_вых и L_s

R_вых = R_v + R_a ; R_a = r₂ + r₁n² ; L_s = L_s2 + L_s1n² ,

где R_v – прямое сопротивление диода одной фазы выпрямления ; R_а – вы − ходное активное сопротивление трансформатора , приведенное к фазе вторичной обмотки ; L_s – индуктивность рассеяния , приведенная к фазе вторичной обмотки ; r₁ , r₂ , L_s1 , L_s2 – активные сопротивления и индук − тивности рассеяния первичной и вторичной обмоток ; n – коэффициент трансформации .

Результат действия активного сопротивления потерь – снижение вели − чин среднего значения напряжения и тока . Действие индуктивности рассеяния сложнее . Согласно графикам U и i₀ на рис . 8 ,б первый по − лупериод – рабочий для V1 .В идеале в момент ωt = π должно произойти мгновенное выключение V1 и выключение V2 . Но из-за индуктивности рассеяния процесс переключения тока затягивается . В одной фазе

э.д.с. рассеяния поддерживает уменьшающийся ток , в другой − препят − ствует . Таким образом , коммутация тока будет происходить за конечный интервал времени . Соответствующий этому интервалу фазовый угол γ

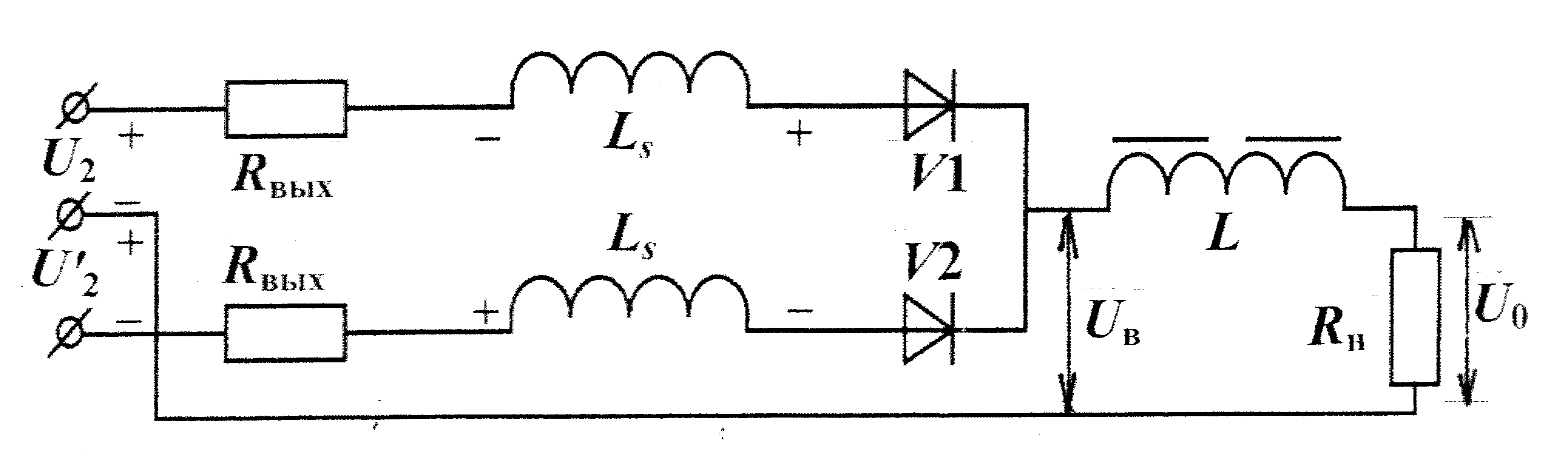
а

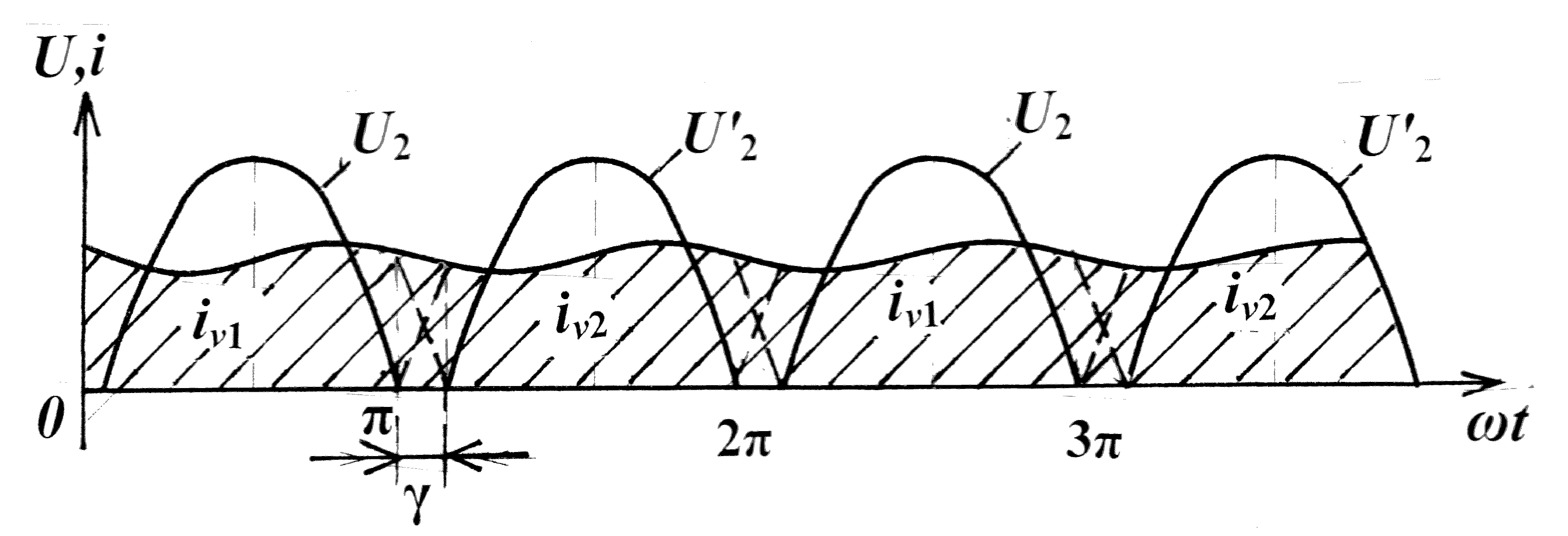
б

Рис. 8

называют углом перекрытия , или коммутации . Чем больше ток нагрузки и L_s , тем больше γ .

Перекрытие токов фаз явление нежелательное , т. к. при этом крайние выводы вторичной обмотки (на рис . 8 , а верхний и нижний) оказыва − ются соединенными через открытые , на этот промежуток времени , дио − ды V1 и V2 . Это явление характерно для многофазных выпрямителей и учитывается дополнительным сопротивлением потерь X_s = ωL_s (сопротив − ление индуктивности рассеяния) .

Падение напряжения на индуктивности рассеяния в общем случае определяется по формуле

,

где m – число фаз выпрямления , ω_с – частота напряжения питающей сети , сек/рад .

При L_s = 0 перекрытие токов фаз отсутствует и ΔU_L = 0 . Если же L_s > 0 , то суммарное падение напряжения потерь

ΔU_потерь = I₀(R_v + R_a) + I₀mfL_s .

Таким образом , постоянная составляющая выпрямленного напряжения в режиме холостого хода (х.х)

U_0.xx = U₀ + I₀(R_v + R_a + mfL_s) ,

С учетом падения напряжения на активном сопротивлении дросселя R_d

U_0.xx = U₀ + I₀(R_v + R_a + R_d + mfL_s) ?

отсюда постоянная составляющая напряжения нагрузки

U₀ = U_0xx – I₀(R_v + R_a + R_d + mfL_s) .

2 . ФИЛЬТРЫ ИСТОЧНИКОВ ПИТАНИЯ

2.1 Общие положения

Основными показателями качества фильтров являются коэффициенты пульсации и сглаживания пульсации . Коэффициенты позволяют сравни − вать уровни переменной составляющей выпрямленного напряжения на входе фильтра и на выходе (или до установки фильтра в цепь нагрузки и после) . Оценим сначала уровни пульсации выпрямленного напряжения на активной нагрузке для разных схем выпрямления , заодно дадим оп − ределение коэффициентам пульсации и сглаживания .

Положим , что напряжение питания имеет синусоидальную форму . В этом случае выпрямленное напряжение u_в на активной нагрузке много − фазного выпрямителя (m = 2 , 3 ,…) описывается рядом

u_в = U₀ + .

Здесь : первое слагаемое ряда U0 – постоянная составляющая напряжения u_в

U₀ = ,

второе слагаемое – переменная составляющая напряжения u_в , причем U_к – амплитуда к – той гармоники ряда

U_k = ,

U_m – амплитуда напряжения , питающего выпрямитель , ω – частота сети , m – число фаз выпрямления , φ_к – фазовый сдвиг к- той гармоники , к – номер гармоники .

Таким образом , u_в содержит помимо постоянной составляющей U₀ ряд гармонических составляющих , из которых первая гармоника имеет наибольшую амплитуду . В частности , при m = 2 U_1~ ≈ 0,67U₀ , U_2~ ≈ 0,13U₀ , U_3~ ≈ U₀ и т. д. . Поскольку амплитуда первой гармоники с час – той mω = 2ω много больше , второй и остальных высших , в дальнейшем будем считать , что первая гармоника определяет в целом параметры пульсации : амплитуду U_1~ ≈ U_~ и частота mω (или mf) . Очевидно , в выпрямителе с двумя фазами выпрямления при частоте питающей сети f = 50Гц , частота пульсации 2∙50 = 100Гц ; при f = 400Гц , частота пуль − сации 2∙400 = 800Гц и т. д. .

Коэффициент пульсации выпрямленного напряжения определяется как отношение амплитуды первой гармоники U_1~ = U_~ к постоянной состав − ляющей U₀

, или в процентах .

При чисто активной нагрузке коэффициенты пульсации по напряже − нию и току одинаковы , что видно из соотношений

U₀ = I₀∙R_н , U_~ = I_~∙R_н , .

В зависимости от назначения электронной аппаратуры допустимая величина коэффициента пульсации колеблется в пределах 0,1…0,0001%.

Отсюда следует необходимость применения сглаживающих фильтров , т. к. коэффициент пульсации напряжения U_в может оказаться неприемлемо большим . Например у выпрямителей : с тремя фазами выпрямления S₀ = 25% , с шестью фазами S₀ = 5,7% , с двенадцатью – S₀ = 1,4% .

Свойство фильтра уменьшать пульсацию напряжения на нагрузке оценивается коэффициентом сглаживания пульсации

,

где S₀ S′₀ − коэффициенты пульсации до и после сглаживающего филь − тра соответственно .

Примечание . Отдельно представим разложение в ряд Фурье напря − жения на нагрузке однофазного однополупериодного выпрямителя (рис. 2)

.

И первая и вторая гармонические составляющие ряда велики . Если оценивать S0 только по первой гармонике , то S0 = 1,57 , т. е. много больше единицы . Сглаживать напряжение (ток) такой формы без ухуд − шения режима работы трансформатора , элементов выпрямителя и филь − тра сложно . Поэтому однофазный однополупериодный выпрямитель имеет ограниченное применение . К фильтру , как к узлу источника пи − тания , предъявляются следующие требования .

Фильтр не должен :

а) нарушать нормальную работу выпрямителя .

б) вносить искажения и помехи в работу электронной аппаратуры .

Потери в фильтре должны быть минимальными , а вес , размеры и стоимость наименьшими . Чтобы избежать резонансных явлений в цепи нагрузки , собственная частота фильтра должна существенно отличаться от частоты переменной составляющей выпрямленного напряжения .

Сглаживающие фильтры делят на :

а) простые , в том числе , индуктивный L и емкостный С фильтры ;

б) сложные - LC и RC , в том числе , однозвенные , многозвенные , ре − зонансные и др. .

Особую группу представляют электронные фильтры , которые содер − жат активные элементы – транзисторы , операционные усилители . В ра − ботах предполагается рассмотреть работу выпрямителей на нагрузку с С , L , LC − фильтрами .