2.6 Короткочасне (віконне) перетворення Фур'є.

Проблеми спектрального аналізу і синтезу сигналів, обмежених у часі, частково вирішуються переходом до так званого короткочасного або віконного перетворення Фур'є. Ідея цього перетворення: часовий інтервал існування сигналу розбивається на ряд проміжків - тимчасових вікон. У кожному проміжку обчислюється своє перетворення Фур'є. Якщо в якомусь вікні існували частотні складові деякого сигналу, то вони будуть присутні в спектрі. А якщо ні - будуть відсутні. Таким чином, можна перейти до частотно-тимчасового подання сигналів, яке є особливим розділом техніки в обробці сигналів.

Короткочасне (віконне) перетворення виконується з використанням виразу:

(2.6)

Тут, на відміну інтеграла Фур'є, функція під знаком інтеграла додатково множиться на віконну функцію . Параметр вікна задає його зрушення на тимчасовій осі. Зазвичай задається ряд фіксованих значень в межах повного вікна. Наприклад, для найпростішого прямокутного вікна функція в межах вікна дає 1, а за межами вікна перегляду - 0. При цьому, для кожного вікна ми отримуємо свій набір комплексних амплітуд сигналу в частотній області.

Природно, що оскільки кожне вікно охоплює невелику ділянку по часу, точність опису зміни сигналу може бути підвищена. Часто використовується вікна Гаусса, чи інші вікна, що забезпечують малі спотворення спектра через граничних явищ і зменшують прояв ефекту Гіббса.

Вона впирається в відомий принцип невизначеності Гейзенберга. Згідно з ним, неможливо отримати одночасно високо частотне і високо тимчасовий дозвіл. Вибираючи вікно з малою шириною по часу, ми отримуємо високий тимчасовий дозвіл, але низький частотний дозвіл. Взявши вікно з великою шириною в часі, отримуємо хороший дозвіл по частоті, але поганий в часі. Віконне перетворення оперує з вікнами, які мають однакову ширину, а потім дане протиріччя для нього є нерозв'язаним. Відзначимо ще один принциповий недолік віконного перетворення Фур'є: в ньому як і раніше використовується єдина базисна функцій - синусоїда з усіма її відзначеними раніше недоліками.

2.7. Функції віконного спектрального аналізу в Mathcad.

Mathcad має ряд функцій віконного спектрального аналізу. Вони дозволяють повністю розбити сигнал на діапазони (вікна) як без перекриття, так і з перекриттям і виконати спектральний аналіз наступного типу:

( , , [, ]) - розрахунок середньої спектральної потужності сигналу

- розрахунок крос-спектра сигналу ;

- розрахунок когерентності сигналів;

- розрахунок відношення сигнал / шум для векторів і .

Завдання 2.7.

Провести порівняння функцій , , , , при:

Рішення:

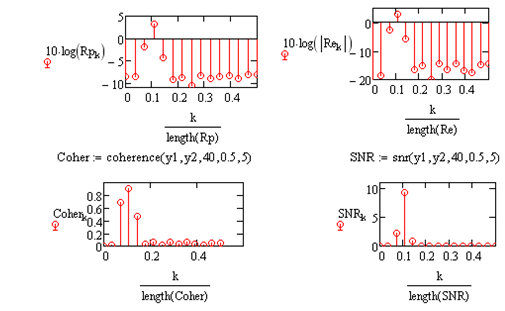
Рис. 2.6. Порівняння спеціальних функцій спектрального аналізу.

У цих функціях і - вектори з комплексними або речовими елементами, - число під діапазонів вхідного сигналу (лежить в межах від 1 до довжини вектора х), - фактор перекриття піддіапазонів (від 0 до 1) і - код вікна, обираний наступним чином:

1. -прямокутне вікно;

2. - вікно типу трапеціі;

3. - трикутне вікно;

4. - вікно Хеннінг;

5. -вікно Хеммінга;

6. -вікно Блекман;