2.5 Віконне перетворення Фур'є. Обмеження і недоліки перетворення Фур'є.

Вейвлет-перетворення істотно складніше, ніж перетворення Фур'є. Тому для практичного застосування вейвлетів важливо чітко зрозуміти відмінності між цими перетвореннями. Основоположна відмінність - втрата інформації і часу існування частотних компонент сигналу при звичайному Фур'є - перетворенні.

В основі представлення періодичного сигналу 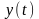рядом Фур'є лежить співвідношення:

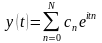(2.4)

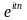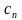де - уявна одиниця Функції представляється сумою добутків синосоїд, представлених членом , на коефіцієнти Фур'є Вони обчислюються як:

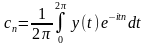(2.5)

Коефіцієнти Фур'є - комплексні числа. Вони представляють набір (спектр) гармонічних сигналів, званих гармоніками. Число - набір гармоніки ( ..).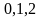

Теоретично ряд Фур'є має нескінченне число членів (гармоніки), але на практиці воно завжди звичайно і одно . Тому ряд (2.4) записується як наближений. Гармоніки, що представляють собою синусоїди з різною частотою, кратною частоті першої гармоніки, і різної фазою, утворюються множенням на .

З позиції точного уявлення перетворенням Фур'є довільних сигналів і функцій можна відзначити цілий ряд його недоліків:

• Незастосовність до аналізу нестаціонарних сигналів;

• Перетворення Фур'є навіть для однієї заданої частоти вимагає знання сигналу не тільки в минулому, але і в майбутньому, що є теоретичною абстракцією;

• В умовах практично неминучого обмежена частота гармонік або спектру коливань точне відновлення сигналу після прямого і зворотного перетворень Фур'є теоретично (і, тим більше, практично) неможливо, зокрема, через появу ефекту Гіббса;

• Базисною функцією при розкладанні в ряд Фур'є є гармонійне (синусоїдальна) коливання, яке математично визначено в інтервалі часу від - ∞ до ∞ і має незмінні в часі параметри.

• Чисельне інтегрування в тимчасовій області від до при прямому перетворенні Фур'є (ППФ) і від до в приватній області при зворотному перетворенні Фур'є (ЗПФ) зустрічається великі обчислювальні труднощі;

• Окремі особливості сигналу (розриви, піки) викликають незначні зміни частотного способу сигналу у всьому інтервалі частот, які «розмазуються» по всій частотній осі, що робить їх виявлення за спектром практично неможливим;

• Така плавна базисна функція, як синусоїда, в принципі не може представляти перепади сигналів з нескінченною крутістю (прямокутні імпульси та ін), хоча такі сигнали застосовуються досить широко;

• Єдиним пристосуванням до уявлення швидких змін сигналів, таких як піки або перепади, є різке збільшення числа гармонік, які впливають на форму сигналу і за межами локальних особливостей сигналу;

• За складом вищих складових спектра практично неможливо оцінити місце розташування особливостей на тимчасовій залежності сигналу і їх характер;

• Для нестаціонарних сигналів (а таких зараз більшість), труднощі ППФ і ОПФ (і ШПФ відповідно) багаторазово зростають.

Завдання 2.6.

Необхідно реалізувати пряме і зворотне ПФ для синусоїди зі сходинками, при:

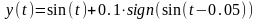
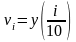
Рішення:

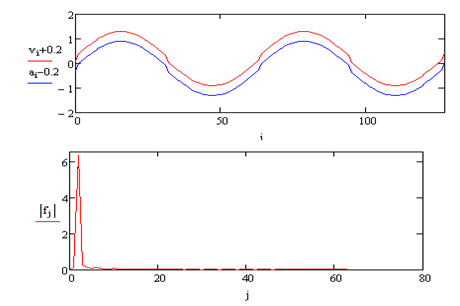
Рис. 2.5. Спектральний аналіз та синтез синусоїдального сигналу з невеликими сходинками при переході через нуль.

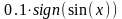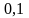Невеликі розриви (сходинки) на синусоїдальному або будь-якому плавно змінюючому сигналі важко виявити в його Фур'є-спектрі, бо вони створюють безліч вищих гармонік дуже малої амплітуди (Рис. 2.5.). Сигнал тут отриманий підсумовуванням синусоїди з меандром, який моделюється виразом вигляду . Таким чином, сходинка має величину від амплітуди синусоїди: і видно на осцилограмі сигналу і його реставрації (для усунення злиття криві розсунули по вертикалі).

Спектр таких сигналів містить ледь помітні високочастотні складові спектру, за якими розпізнати локальну особливість сигналу і, тим більше, її місце і характер, практично неможливо. Складові спектру особливості як би розмазані по осі частот.